青岛版八年级数学上册1.2.2 怎样判定三角形全等 教学课件(共18张PPT)
文档属性
| 名称 | 青岛版八年级数学上册1.2.2 怎样判定三角形全等 教学课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 09:29:50 | ||
图片预览



文档简介
(共18张PPT)
01
学习目标
05
随堂练习
06
课堂小结
03
新知探究
02
旧知回顾
04
例题精讲
1.掌握ASA的内容,能应用角边角定理证明两个三角形全等;
2.掌握AAS的内容,并能应用角角边定理证明两个三角形全等。
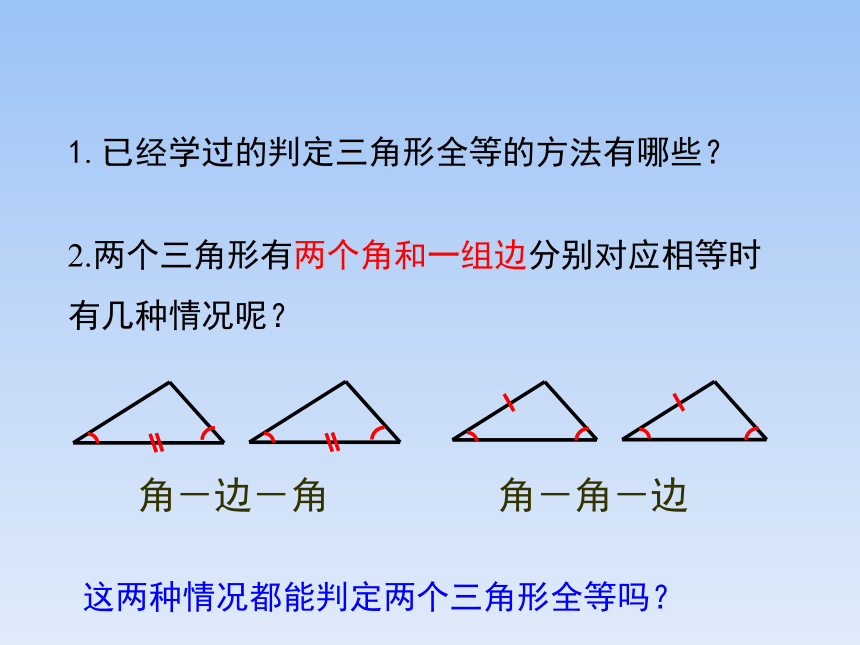
1.已经学过的判定三角形全等的方法有哪些?
2.两个三角形有两个角和一组边分别对应相等时有几种情况呢?
这两种情况都能判定两个三角形全等吗?
角-边-角
角-角-边
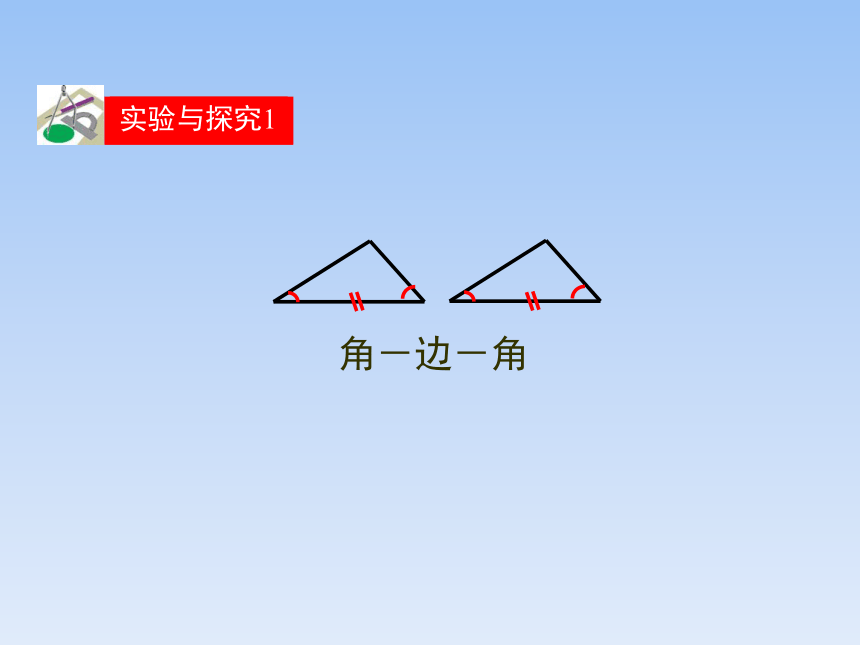
实验与探究1
角-边-角
判定方法2:
两角及其夹边分别相等的两个三角形全等.
简写成“角边角”或“ASA”.
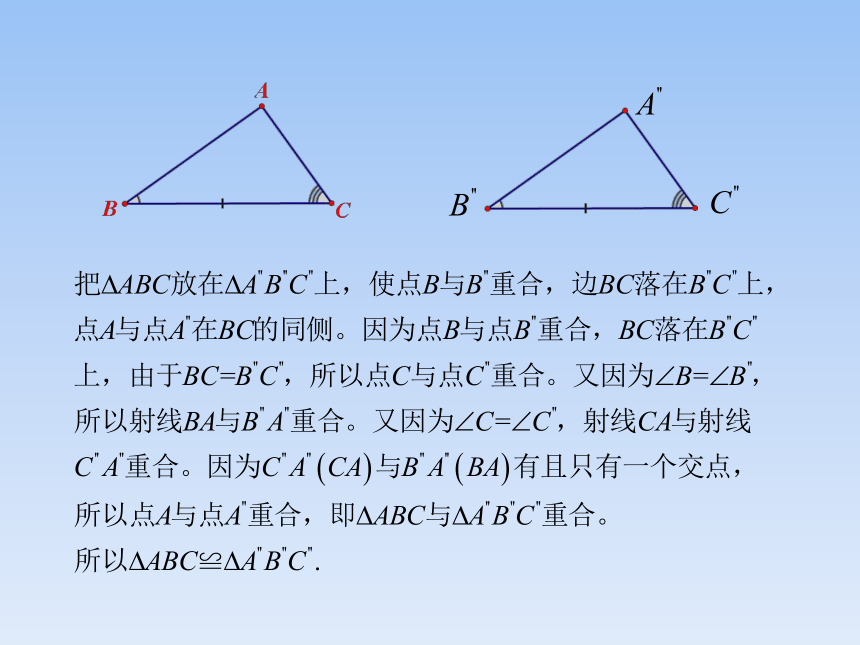
如图,在△ABC与△A’’B’’C’’中
∴△ABC≌△A’’B’’C’’(ASA).
BC=B’’C’’,
∵∠B=∠B’’,
∠C=∠C’’,
提示:登录优教同步学习网,搜索动画演示:两个三角形全等的判定方法(ASA)
小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢 如果可以,带哪块去合适呢 为什么
想一想:
角-角-边
实验与探究2
做一做:按要求画三角形,并与同伴交流.
已知:∠A=600、∠B=450、BC=3cm
B
C
A
750
450
3cm
剪下来,与同伴进行比较,它们能否互相重合?
600
判定方法3:
两角分别相等且其中一组等角的对边也相等的两个三角形全等.
常简写成“角角边” 或“ AAS”.
如图,在△ABC与△DEF中
∴△ABC≌△DEF(AAS).
BC=EF,
∵∠A=∠D,
∠B=∠E,
E
F
D
B
A
C
提示:登录优教同步学习网,搜索动画演示:两个三角形全等的判定方法(AAS)
例3 如图1-13,已知∠ACB=∠DFE,∠B=∠E,BC=EF那么△ABC与△DEF全等吗?为什么?
解: △ABC与△DEF全等.
理由是:
在△ABC与△DEF中,
∵∠ACB=∠DFE,∠B=∠E,
BC,EF分别是∠B 与∠ACB, ∠E与∠DFE的夹边,且BC=EF,
由ASA,所以△ABC≌△DEF.
例4 如图1-15,在△ABD与△CDB中,已知∠A=∠C,再添加一个什么条件,就可以判定△ABD与△CDB全等?
解: 由已知∠A=∠C,BD=DB,再添加∠1=∠2(或∠3=∠4),就可以判定△ABD与△CDB全等.
理由:在△ABD与△CDB中,因为∠A=∠C,∠1=∠2 (或∠3=∠4),BD分别是∠A和∠C的对边,又是△ABD与△CDB的公共边,BD=DB,
由AAS,所以△ABD ≌ △CDB.
1.如图,为测量河宽AB,小军从河岸的A点沿着与AB垂直的方向走到C点,并在AC的中点E处立一根标杆,然后从C点沿着和AC垂直的方向走到D点,使点D,E,B恰好在一条直线上.于是小军说:“CD的长就是河的宽度.”你能说出这个道理吗?
A
B
E
C
D
2.已知:如图,AD=BE, ∠A=∠FDE,BC∥EF.
求证:△ABC≌△DEF.
C
A
B
D
F
E
3.已知:如图,点B,F,C,E在同一条直线上,
AC∥FD,∠A=∠D,BF=EC. 求证:∠B=∠E.
(1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
知识要点:
(3)探索三角形全等是证明线段相等(对应边相等),角相等(对应角相等)等问题的基本途径。
数学思想:
要学会用分类的思想,转化的思想解决问题。
作 业
P16习题1.2 T3、4、5.
01
学习目标
05
随堂练习
06
课堂小结
03
新知探究
02
旧知回顾
04
例题精讲
1.掌握ASA的内容,能应用角边角定理证明两个三角形全等;
2.掌握AAS的内容,并能应用角角边定理证明两个三角形全等。
1.已经学过的判定三角形全等的方法有哪些?
2.两个三角形有两个角和一组边分别对应相等时有几种情况呢?
这两种情况都能判定两个三角形全等吗?
角-边-角
角-角-边
实验与探究1
角-边-角
判定方法2:
两角及其夹边分别相等的两个三角形全等.
简写成“角边角”或“ASA”.
如图,在△ABC与△A’’B’’C’’中
∴△ABC≌△A’’B’’C’’(ASA).
BC=B’’C’’,
∵∠B=∠B’’,
∠C=∠C’’,
提示:登录优教同步学习网,搜索动画演示:两个三角形全等的判定方法(ASA)
小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢 如果可以,带哪块去合适呢 为什么
想一想:
角-角-边
实验与探究2
做一做:按要求画三角形,并与同伴交流.
已知:∠A=600、∠B=450、BC=3cm
B
C
A
750
450
3cm
剪下来,与同伴进行比较,它们能否互相重合?
600
判定方法3:
两角分别相等且其中一组等角的对边也相等的两个三角形全等.
常简写成“角角边” 或“ AAS”.
如图,在△ABC与△DEF中
∴△ABC≌△DEF(AAS).
BC=EF,
∵∠A=∠D,
∠B=∠E,
E
F
D
B
A
C
提示:登录优教同步学习网,搜索动画演示:两个三角形全等的判定方法(AAS)
例3 如图1-13,已知∠ACB=∠DFE,∠B=∠E,BC=EF那么△ABC与△DEF全等吗?为什么?
解: △ABC与△DEF全等.
理由是:
在△ABC与△DEF中,
∵∠ACB=∠DFE,∠B=∠E,
BC,EF分别是∠B 与∠ACB, ∠E与∠DFE的夹边,且BC=EF,
由ASA,所以△ABC≌△DEF.
例4 如图1-15,在△ABD与△CDB中,已知∠A=∠C,再添加一个什么条件,就可以判定△ABD与△CDB全等?
解: 由已知∠A=∠C,BD=DB,再添加∠1=∠2(或∠3=∠4),就可以判定△ABD与△CDB全等.
理由:在△ABD与△CDB中,因为∠A=∠C,∠1=∠2 (或∠3=∠4),BD分别是∠A和∠C的对边,又是△ABD与△CDB的公共边,BD=DB,
由AAS,所以△ABD ≌ △CDB.
1.如图,为测量河宽AB,小军从河岸的A点沿着与AB垂直的方向走到C点,并在AC的中点E处立一根标杆,然后从C点沿着和AC垂直的方向走到D点,使点D,E,B恰好在一条直线上.于是小军说:“CD的长就是河的宽度.”你能说出这个道理吗?
A
B
E
C
D
2.已知:如图,AD=BE, ∠A=∠FDE,BC∥EF.
求证:△ABC≌△DEF.
C
A
B
D
F
E
3.已知:如图,点B,F,C,E在同一条直线上,
AC∥FD,∠A=∠D,BF=EC. 求证:∠B=∠E.
(1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
知识要点:
(3)探索三角形全等是证明线段相等(对应边相等),角相等(对应角相等)等问题的基本途径。
数学思想:
要学会用分类的思想,转化的思想解决问题。
作 业
P16习题1.2 T3、4、5.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
