青岛版八年级数学上册 1.2怎样判定三角形全等 导学案(无答案)
文档属性
| 名称 | 青岛版八年级数学上册 1.2怎样判定三角形全等 导学案(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 135.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 09:34:13 | ||
图片预览

文档简介
§1.2 怎样判定三角形全等 导学案
【学习目标】
1、知识与技能 掌握“边角边”这一三角形全等的判定方法
2、过程与方法 经历探究三角形全等的判定方法的过程,学会解决一些简单的实际问题
3、情感、态度与价值观 培养合情推理能力,感悟三角形全等的应用价值
【学习重点】探究“边角边”这一判定方法,以及这一方法的应用.
【学习难点】让同学们了解三角形全等中“边边角”的辨析.
【学具准备】剪刀、三角板、直尺、长方形的纸片等
【学习过程】
(一)知识引桥
1、什么叫全等三角形?
2、全等三角形有什么性质?
3、若△ABC≌△DEF,点A与点D,点B与点E是对应点,试写出其中相等的线段和角.
问题1:在△ABC和△DEF中,AB=DE,BC=EF,AC=DF, ∠A=∠D, ∠B=∠E, ∠C=∠F,则△ABC和△DEF全等吗
问题2: △ABC和△DEF全等是不是一定要满足AB=DE,BC=EF,AC=DF, ∠A=∠D, ∠B=∠E, ∠C=∠F这六个条件呢?若满足这六个条件中的一个、两个或三个条件,这两个三角形全等吗 请同学们完成下面的探究活动
(二)探究活动: (小组内合作交流)
1、只知道一条边相等的两个三角形一定全等吗?只知道一个角相等的两个三角形一定全等吗?
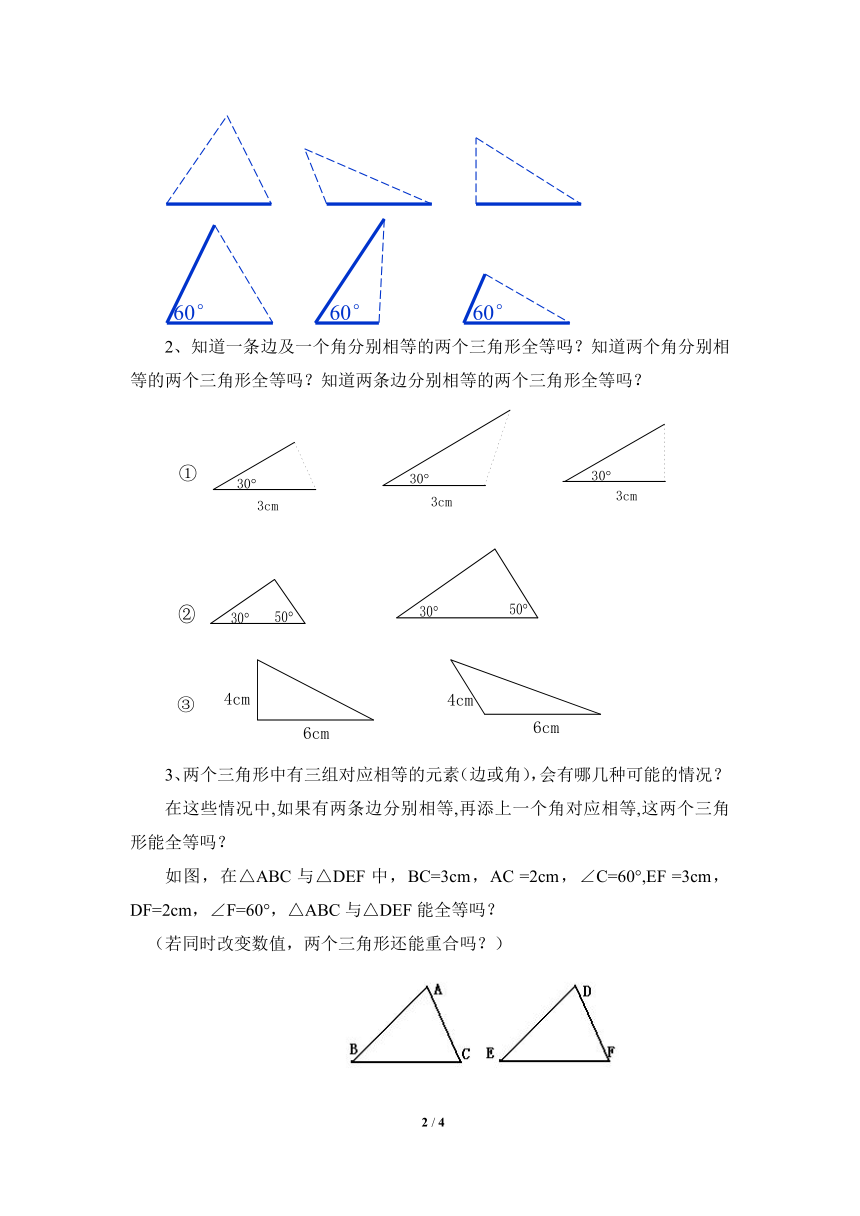
2、知道一条边及一个角分别相等的两个三角形全等吗?知道两个角分别相等的两个三角形全等吗?知道两条边分别相等的两个三角形全等吗?
3、两个三角形中有三组对应相等的元素(边或角),会有哪几种可能的情况?
在这些情况中,如果有两条边分别相等,再添上一个角对应相等,这两个三角形能全等吗?
如图,在△ABC与△DEF中,BC=3cm,AC =2cm,∠C=60°,EF =3cm,DF=2cm,∠F=60°,△ABC与△DEF能全等吗?
(若同时改变数值,两个三角形还能重合吗?)
由上面的探究活动猜想并归纳:
在两个三角形中,必须具备 对元素分别相等,才能保证两个三角形全等.
判定方法1:
的两个三角形全等.通常简写成 .
注意:在△ABC与△DEF中,若AB=DE,AC=DF,∠B=∠E,观察△ABC与△DEF是否全等.为什么
结论:
.
(三)学以致用
1、如图,AB=AD,∠BAC=∠DAC,
问题1:△ABC和△ADC全等吗?
问题2:它们已经有了哪些元素对应相等?
问题3:还缺什么条件?
2、如图,为了测量池塘边上A、B两点之间的距离,小亮设计了一个方案:先在平地上取一个能够直接到达A和B的点C,然后在射线AC上取一点D,使CD=CA,在射线BC上取一点E,使CE=CB,连接DE,那么线段DE的长就等于A、B两点之间的距离,你认为他的方案对吗?为什么?
(四)巩固练习
1、如图,已知∠CAB=∠DAB,请你添加一个条件,使得△ABC≌△ABD.
2、已知:AB=AD,AC=AE,△ABE和△ADC全等吗?为什么?
3、如图,E,F在BC上,BE=CF,AB=CD,AB∥CD,说明:△ABF≌ △DCE
参考答案:
1、AC=AD
2、全等,由∠A=∠A,根据SAS得出
3、根据SAS得出
【自我反思】
本节课你的收获是什么?
60°
60°
60°
A
C
D
B
4 / 4
【学习目标】
1、知识与技能 掌握“边角边”这一三角形全等的判定方法
2、过程与方法 经历探究三角形全等的判定方法的过程,学会解决一些简单的实际问题
3、情感、态度与价值观 培养合情推理能力,感悟三角形全等的应用价值
【学习重点】探究“边角边”这一判定方法,以及这一方法的应用.
【学习难点】让同学们了解三角形全等中“边边角”的辨析.
【学具准备】剪刀、三角板、直尺、长方形的纸片等
【学习过程】
(一)知识引桥
1、什么叫全等三角形?
2、全等三角形有什么性质?
3、若△ABC≌△DEF,点A与点D,点B与点E是对应点,试写出其中相等的线段和角.
问题1:在△ABC和△DEF中,AB=DE,BC=EF,AC=DF, ∠A=∠D, ∠B=∠E, ∠C=∠F,则△ABC和△DEF全等吗
问题2: △ABC和△DEF全等是不是一定要满足AB=DE,BC=EF,AC=DF, ∠A=∠D, ∠B=∠E, ∠C=∠F这六个条件呢?若满足这六个条件中的一个、两个或三个条件,这两个三角形全等吗 请同学们完成下面的探究活动
(二)探究活动: (小组内合作交流)
1、只知道一条边相等的两个三角形一定全等吗?只知道一个角相等的两个三角形一定全等吗?
2、知道一条边及一个角分别相等的两个三角形全等吗?知道两个角分别相等的两个三角形全等吗?知道两条边分别相等的两个三角形全等吗?
3、两个三角形中有三组对应相等的元素(边或角),会有哪几种可能的情况?
在这些情况中,如果有两条边分别相等,再添上一个角对应相等,这两个三角形能全等吗?
如图,在△ABC与△DEF中,BC=3cm,AC =2cm,∠C=60°,EF =3cm,DF=2cm,∠F=60°,△ABC与△DEF能全等吗?
(若同时改变数值,两个三角形还能重合吗?)
由上面的探究活动猜想并归纳:
在两个三角形中,必须具备 对元素分别相等,才能保证两个三角形全等.
判定方法1:
的两个三角形全等.通常简写成 .
注意:在△ABC与△DEF中,若AB=DE,AC=DF,∠B=∠E,观察△ABC与△DEF是否全等.为什么
结论:
.
(三)学以致用
1、如图,AB=AD,∠BAC=∠DAC,
问题1:△ABC和△ADC全等吗?
问题2:它们已经有了哪些元素对应相等?
问题3:还缺什么条件?
2、如图,为了测量池塘边上A、B两点之间的距离,小亮设计了一个方案:先在平地上取一个能够直接到达A和B的点C,然后在射线AC上取一点D,使CD=CA,在射线BC上取一点E,使CE=CB,连接DE,那么线段DE的长就等于A、B两点之间的距离,你认为他的方案对吗?为什么?
(四)巩固练习
1、如图,已知∠CAB=∠DAB,请你添加一个条件,使得△ABC≌△ABD.
2、已知:AB=AD,AC=AE,△ABE和△ADC全等吗?为什么?
3、如图,E,F在BC上,BE=CF,AB=CD,AB∥CD,说明:△ABF≌ △DCE
参考答案:
1、AC=AD
2、全等,由∠A=∠A,根据SAS得出
3、根据SAS得出
【自我反思】
本节课你的收获是什么?
60°
60°
60°
A
C
D
B
4 / 4
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
