北师大版七年级数学下册 4.3 探索三角形全等的条件 课件(共24张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 4.3 探索三角形全等的条件 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 893.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 09:51:31 | ||
图片预览


文档简介
(共24张PPT)
三角形全等的判定
A
B
C
D
E
F
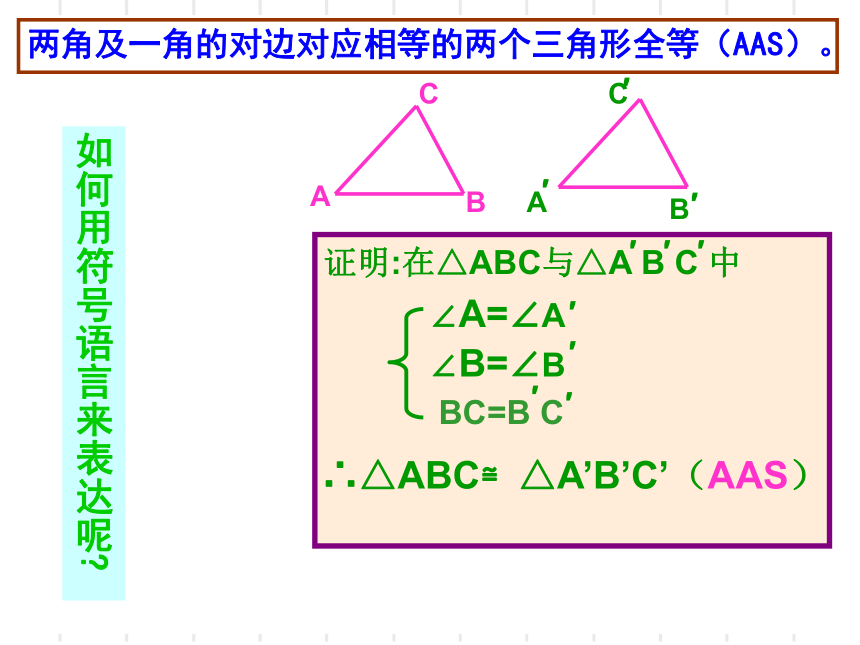
如何用符号语言来表达呢
证明:在△ABC与△A B C 中
∠A=∠A AB=A B
∴△ABC≌△A’B’C’(ASA)
A
C
B
A
′
C
B
′
′
′
′
′
′
′
′
∠B=∠B
′
两角及夹边对应相等的两个三角形全等(ASA).
如何用符号语言来表达呢
证明:在△ABC与△A B C 中
∠A=∠A
∴△ABC≌△A’B’C’(AAS)
A
C
B
A
′
C
B
′
′
′
′
′
′
∠B=∠B
′
′
′
BC=B C
两角及一角的对边对应相等的两个三角形全等(AAS)。
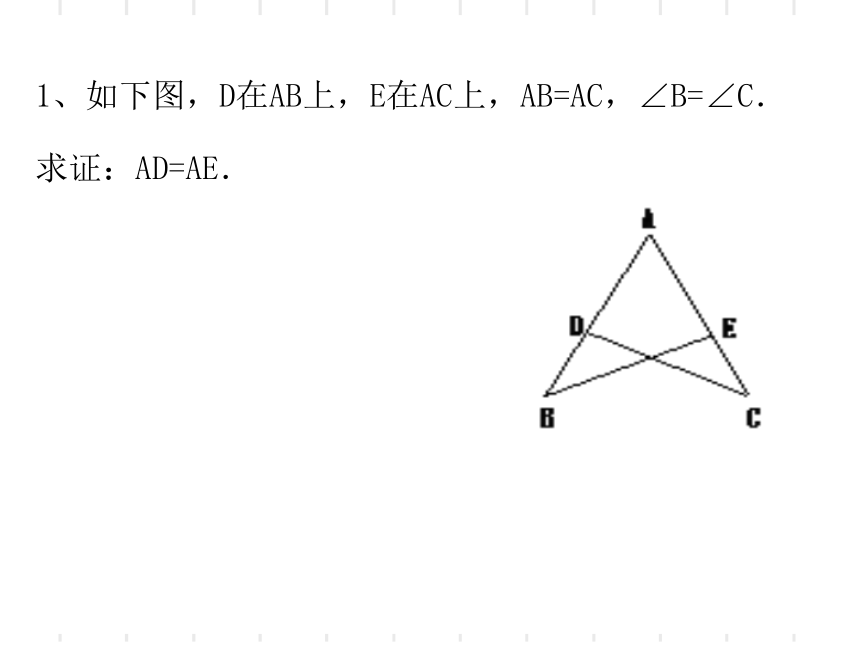
1、如下图,D在AB上,E在AC上,AB=AC,∠B=∠C.
求证:AD=AE.
【规律总结】
说明三角形全等的三类条件
1.直接条件:即已知中直接给出的三角形的对应边或对应角.
2.隐含条件:即已知没有给出,但通过读图很容易得到的条件,如公共边、公共角、对顶角等.
3.间接条件:即已知中所给条件不是三角形的边和角,需要进一步推理.
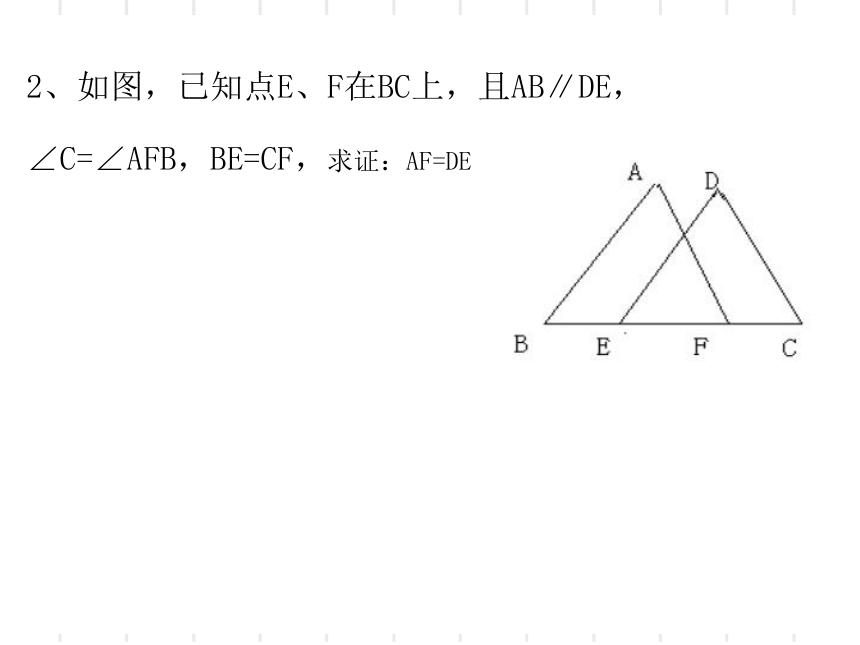
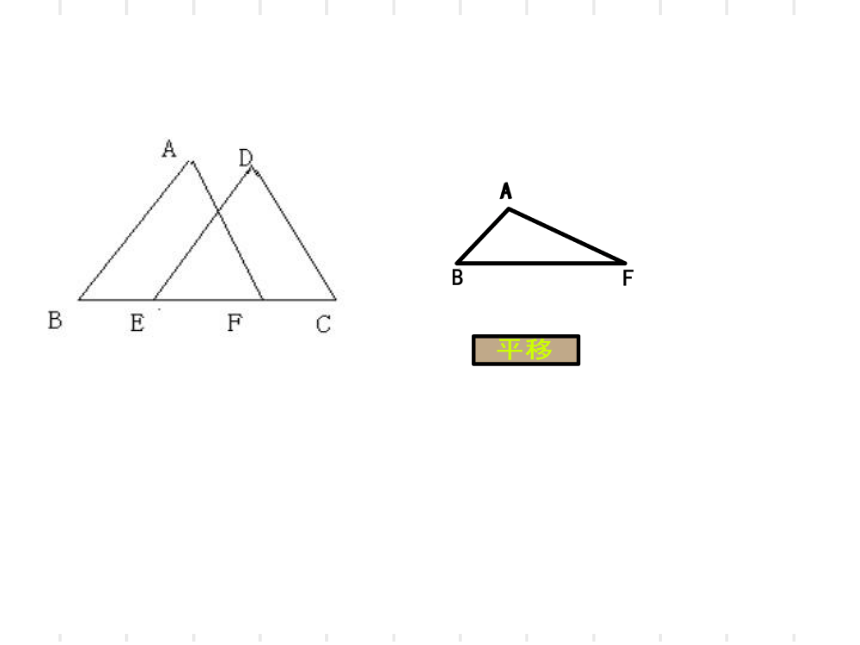
2、如图,已知点E、F在BC上,且AB∥DE,∠C=∠AFB,BE=CF,求证:AF=DE
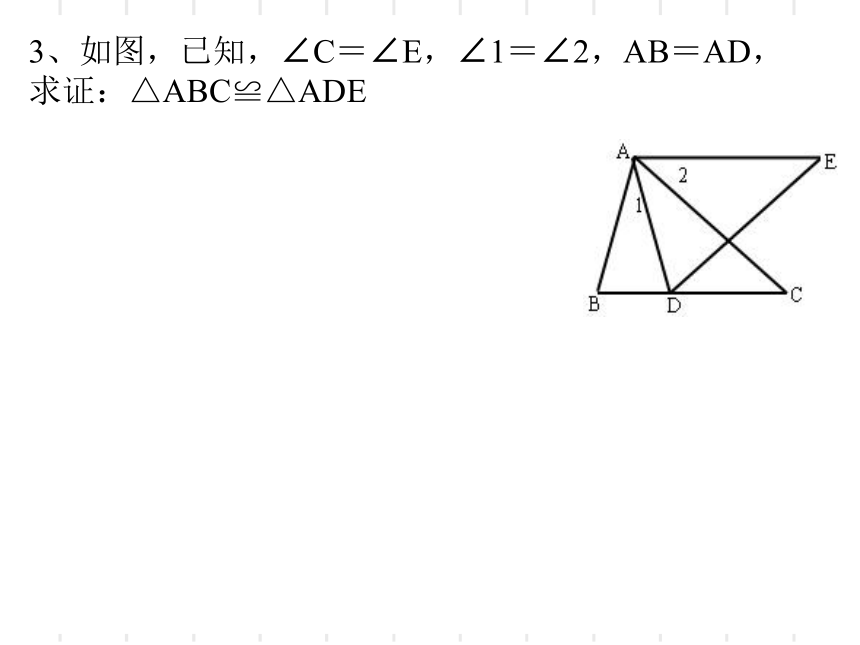
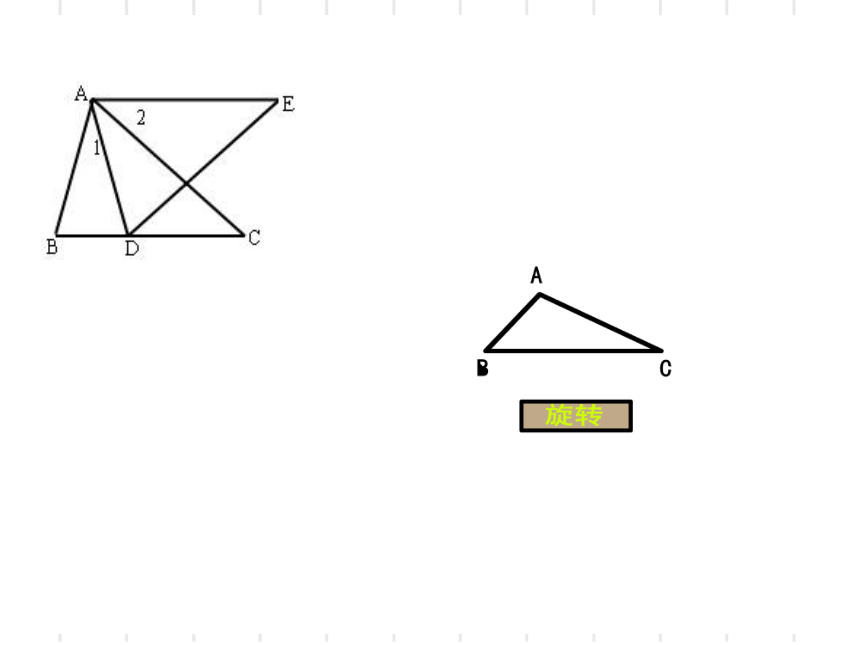
3、如图,已知,∠C=∠E,∠1=∠2,AB=AD,
求证:△ABC≌△ADE
变式一: 已知:如图 , FB=CE , ∠A=∠D , AC∥FD.F、C在直线BE上.
求证:AB=DE , AC=DF.
变式二、如图,点A,B,D,E在同一直线上,AD=EB,
BC∥DF,∠C=∠F.求证:AC=EF.
变式三、如图,O是AB的中点,添加一个适当的条件:___________,使△AOC ≌△BOD(只填一个即可)
A
B
C
D
O
A
B
C
D
O
强者闯关:
变式四、已知:如图,在△MPN中,H是高MQ和NR的
交点,且MQ=NQ.
求证:HN=PM.
如图所示,直线
a经过正方形ABCD的顶点A,分别过正
方形的顶点B,D作BF⊥a于点F,DE⊥a
于点E,若DE=8,BF=5,则EF的长为
_________.
【解析】因为四边形ABCD是正方形,所以AB=AD,
∠ABC=∠BAD=90°.
因为BF⊥a于点F,DE⊥a于点E,
所以∠FAB+∠FBA=∠FAB+∠EAD=90°,所以∠FBA=∠EAD.
所以在Rt△AFB和Rt△AED中,因为∠AFB=∠DEA=90°,∠FBA=∠EAD ,AB=DA,所以△AFB≌△DEA(AAS),
所以AF=DE=8,BF=AE=5,
所以EF=AF+AE=8+5=13.
答案:13
(1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
知识要点:
(3)探索三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径。
数学思想:
要学会用分类的思想,转化的思想解决问题。
三角形全等的判定
A
B
C
D
E
F
如何用符号语言来表达呢
证明:在△ABC与△A B C 中
∠A=∠A AB=A B
∴△ABC≌△A’B’C’(ASA)
A
C
B
A
′
C
B
′
′
′
′
′
′
′
′
∠B=∠B
′
两角及夹边对应相等的两个三角形全等(ASA).
如何用符号语言来表达呢
证明:在△ABC与△A B C 中
∠A=∠A
∴△ABC≌△A’B’C’(AAS)
A
C
B
A
′
C
B
′
′
′
′
′
′
∠B=∠B
′
′
′
BC=B C
两角及一角的对边对应相等的两个三角形全等(AAS)。
1、如下图,D在AB上,E在AC上,AB=AC,∠B=∠C.
求证:AD=AE.
【规律总结】
说明三角形全等的三类条件
1.直接条件:即已知中直接给出的三角形的对应边或对应角.
2.隐含条件:即已知没有给出,但通过读图很容易得到的条件,如公共边、公共角、对顶角等.
3.间接条件:即已知中所给条件不是三角形的边和角,需要进一步推理.
2、如图,已知点E、F在BC上,且AB∥DE,∠C=∠AFB,BE=CF,求证:AF=DE
3、如图,已知,∠C=∠E,∠1=∠2,AB=AD,
求证:△ABC≌△ADE
变式一: 已知:如图 , FB=CE , ∠A=∠D , AC∥FD.F、C在直线BE上.
求证:AB=DE , AC=DF.
变式二、如图,点A,B,D,E在同一直线上,AD=EB,
BC∥DF,∠C=∠F.求证:AC=EF.
变式三、如图,O是AB的中点,添加一个适当的条件:___________,使△AOC ≌△BOD(只填一个即可)
A
B
C
D
O
A
B
C
D
O
强者闯关:
变式四、已知:如图,在△MPN中,H是高MQ和NR的
交点,且MQ=NQ.
求证:HN=PM.
如图所示,直线
a经过正方形ABCD的顶点A,分别过正
方形的顶点B,D作BF⊥a于点F,DE⊥a
于点E,若DE=8,BF=5,则EF的长为
_________.
【解析】因为四边形ABCD是正方形,所以AB=AD,
∠ABC=∠BAD=90°.
因为BF⊥a于点F,DE⊥a于点E,
所以∠FAB+∠FBA=∠FAB+∠EAD=90°,所以∠FBA=∠EAD.
所以在Rt△AFB和Rt△AED中,因为∠AFB=∠DEA=90°,∠FBA=∠EAD ,AB=DA,所以△AFB≌△DEA(AAS),
所以AF=DE=8,BF=AE=5,
所以EF=AF+AE=8+5=13.
答案:13
(1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
知识要点:
(3)探索三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径。
数学思想:
要学会用分类的思想,转化的思想解决问题。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
