2021-2022学年冀教版七年级数学下册 7.5平行线的性质 课时练习(word版 含解析)
文档属性
| 名称 | 2021-2022学年冀教版七年级数学下册 7.5平行线的性质 课时练习(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 318.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 00:00:00 | ||
图片预览




文档简介
平行线的性质
一、单选题
1.下列说法:①两直线平行,同旁内角互补;②内错角相等,两直线平行;③同位角相等,两直线平行;④垂直于同一条直线的两条直线平行,其中是平行线的性质的是( )
A.① B.②和③ C.④ D.①和④
2.如图,ABCD,AD⊥BD,∠1=53°,则∠2的大小是( )
A.53° B.50° C.37° D.23°
3.如图所示,把一个长方形纸片ABCD沿EF折叠后,点D,C分别落在点D,C位置,D'恰好在BC上,若∠,则∠ED'F等于( )
A.45° B.50° C.55° D.60°
4.生活中常见的探照灯、汽车大灯等灯具都与抛物线有关.如图,从光源P点照射到抛物线上的光线等反射以后沿着与直线平行的方向射出,若,,则的度数为( )°
A. B. C. D.
5.一把直尺与一块直角三角板按下图方式摆放,若,则( )
A.52° B.53° C.54° D.63°
6.如图,AB∥CD,AE∥CF,∠C=131°,则∠A=( )
A.39° B.41° C.49° D.51°
7.如图,若AB∥CD,CD∥EF,那么BCE=( )
A.180°-2+1 B.180°-1-2 C.2=21 D.1+2
8.一副三角板摆放如图所示,斜边FD与直角边AC相交于点E,点D在直角边BC上,且FDAB,∠B=30°,则∠ADB的度数是( )
A.95° B.105° C.115° D.125°
9.如果两个角的一边在同一直线上,另一边互相平行,则这两个角( )
A.相等 B.互补 C.互余 D.相等或互补
10.一学员在广场上练习驾驶汽车,两次拐弯后行驶的方向与原来的方向相同,这两次拐弯的角度可能是( ) .
A.第一次向左拐30°,第二次向右拐30°.
B.第一次向右拐50°,第二次向左拐130°.
C.第一次向左拐50°,第二次向左拐130°.
D.第一次向左拐50°,第二次向右拐130°.
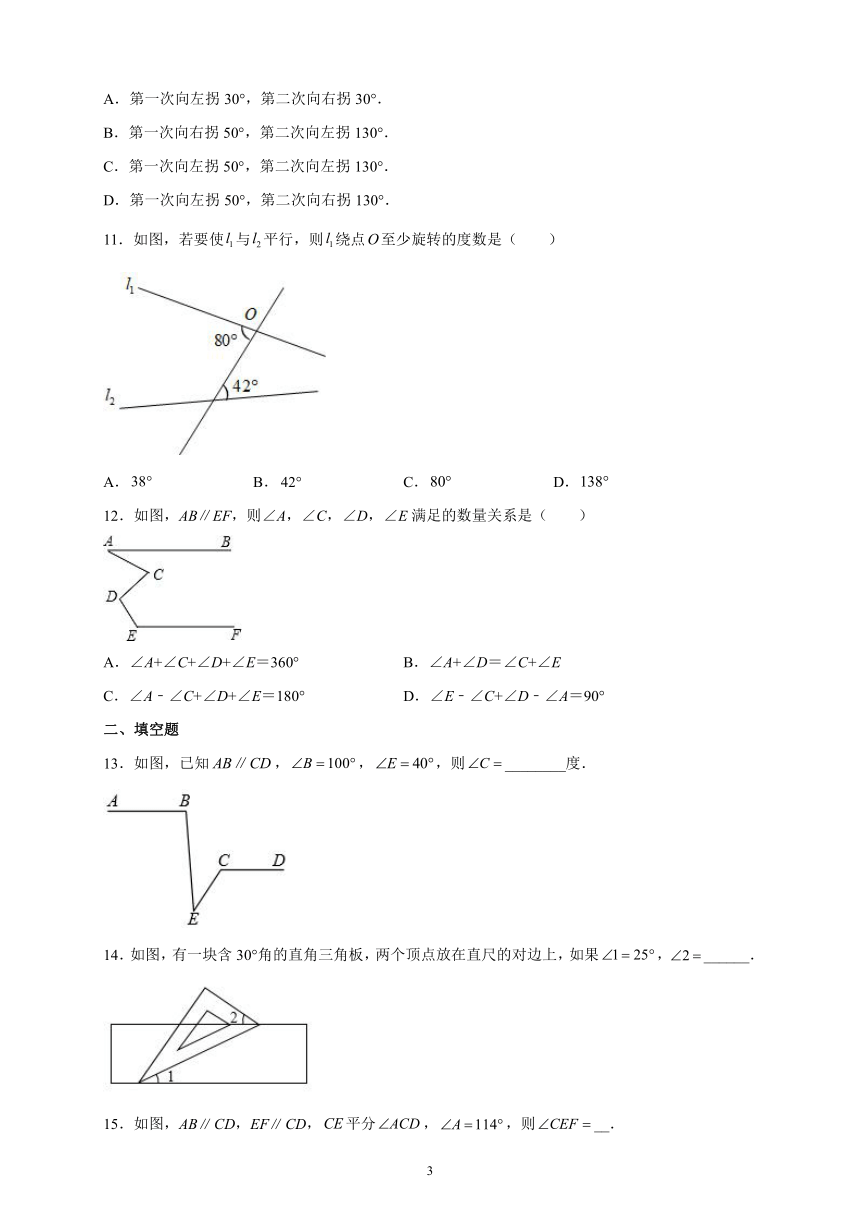
11.如图,若要使与平行,则绕点至少旋转的度数是( )
A. B. C. D.
12.如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A.∠A+∠C+∠D+∠E=360° B.∠A+∠D=∠C+∠E
C.∠A﹣∠C+∠D+∠E=180° D.∠E﹣∠C+∠D﹣∠A=90°
二、填空题
13.如图,已知,,,则________度.
14.如图,有一块含30°角的直角三角板,两个顶点放在直尺的对边上,如果,______.
15.如图,ABCD,EFCD,平分,,则__.
16.如图,直线a与直线b平行,将三角板的直角顶点放在直线a上,若∠1=40°,到∠2=__°.
17.如图,已知AB∥CD,∠ABC=120°,∠1=27°,则直线CB和CE的夹角是_____°.
三、解答题
18.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,∠ACB的度数,并说明理由.
解:OA∥BC,OB∥AC.
理由:∵∠1=50°,∠2=50°,
∴∠1=∠2(等量代换)
∴OB∥AC. ( ),
∴∠3+∠ACB=180°,( ),
∴∠ACB= °,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥BC.( ).
19.如图,ABCD,点E在直线CD上,BG平分∠ABE交CD于点G.
(1)求证:∠BGE=∠GBE;
(2)若∠DEF=70°,求∠FBG的度数.
20.已知:如图,点D、E、F、G都在的边上,,且
(1)求证:;
(2)若EF平分,,求的度数.
21.如图①,直线AB∥CD,点E,F分别在直线AB,CD上.
(1)若∠1=135°,∠2=155°,试猜想∠P=______.
(2)在图①中探究∠1,∠P,∠2之间的数量关系,并证明你的结论.
(3)将图①变为图②,仍有AB∥CD,若∠1+∠2=325°,∠EPG=75°,求∠PGF的度数.
22.请回答下列各题.
(1)探究:如图1,AB∥CD∥EF,试说明∠BCF=∠B+∠F.
(2)应用:如图2,AB∥CD,点F在AB、CD之间,FE与AB交于点M,FG与CD交于点N.若∠EFG=115°,∠EMB=55°,则∠DNG的大小是多少?
(3)拓展:如图3,直线CD在直线AB、EF之间,且AB∥CD∥EF,点G、H分别在直线AB、EF上,点Q是直线CD上的一个动点,且不在直线GH上,连结QG、QH.若∠GQH=70°,则∠AGQ+∠EHQ=______度(请直接写出答案).
试卷第1页,共3页
参考答案:
1.A
解:①是平行线的性质,故符合题意;
②是平行线的判定,故不符合题意;
③是平行线的判定,故不符合题意;
④是平行线的判定,故不符合题意;
故选:A.
2.C
解:∵ABCD,∠1=53°,
∴∠BDC=180°﹣∠1=127°,
∵AD⊥BD,
∴∠ADB=90°,
∴∠2=∠BDC﹣∠ADB=37°.
故选:C.
3.B
解:由题意知AD∥BC,∠EFB=65°,
∴∠DEF=∠EFB=65°,∠ED'F=∠AED′
根据折叠变换的性质知∠D′EF=∠DEF=65°,
则∠AED′=180° ∠DEF ∠D′EF=50°,
∴∠ED'F=50°
故选B.
4.C
解:
故选C
5.B
解:如图,过三角板的直角顶点作直尺两边的平行线,
∵直尺的两边互相平行,
∴,,
∴,
∴,
故选B.
6.C
解:如图,
∵AB∥CD,∠C=131°,
∴∠1 =180°-∠C=49°(两直线平行,同旁内角互补),
∵AE∥CF,
∴∠A=∠C=49°(两直线平行,同位角相等).
故选:C.
7.A
解:∵AB∥CD,CD∥EF,
∴∠1=∠BCD,∠ECD+∠2=180°,
∴BCE=∠BCD+∠ECD=180°-2+1,
故选A.
8.B
解:由题意得∠ADF=45°,
∵,∠B=30°,
∴∠B+∠BDF=180°,
∴∠BDF=180°﹣∠B=150°,
∴∠ADB=∠BDF﹣∠ADF=105°.
故选:B
9.D
解:如图,当AE∥BD时,∠EAB与∠DBC符合题意,
∴∠EAB=∠DBC;
如图,当AE∥BD时,∠EAF与∠DBC符合题意,
∵∠EAB+∠EAF=180°,∠EAB=∠DBC,
∴∠DBC +∠EAF=180°,
故选D.
10.A
解:由第一次向左拐30°,第二次向右拐30°可得转完两次后相当于在原方向上转过了,和原来方向相同,故A正确;
第一次向右拐50°,第二次向左拐130°可得转完两次后相当于在原方向上左拐,故B错误;
第一次向左拐50°,第二次向左拐130°可得转完两次后相当于在原方向上右拐,故C错误;
第一次向左拐50°,第二次向右拐130°可得转完两次后相当于在原方向上右拐,故D错误;
综上所述,符合条件的是A.
故选:A.
11.A
解:如图,
∵l1∥l2,
∴∠AOB=∠OBC=42°,
∴80°-42°=38°,
即l1绕点O至少旋转38度才能与l2平行.
故选:A.
12.C
解:如图,过点C作CG∥AB,过点D作DH∥EF,
∴∠A=∠ACG,∠EDH=180°﹣∠E,
∵AB∥EF,
∴CG∥DH,
∴∠CDH=∠DCG,
∴∠ACD=∠ACG+∠CDH=∠A+∠CDE﹣(180°﹣∠E),
∴∠A﹣∠ACD+∠CDE+∠E=180°.
故选:C.
13.110
解:过E作一条直线
∵,,
∴,
∵,,
∴,
∴
又∵,
∴.
故答案为:110.
14.##35度
解:如图,根据题意可知,
∴,
∴.
故答案为:.
15.##147度
解:,
,
,
.
平分,
.
,
,
.
故答案为:.
16.50
解:如图
∵
∴∠2=∠3
∵∠1+∠3=90°,∠1=40°
∴
∴∠2=50°
故答案为;50.
17.93
解:∵AB∥CD
∴∠DCB=∠ABC=120°
又∵∠1=27°
∴∠BCE=∠DCB -∠1=93°
故答案为93.
18.同位角相等,两直线平行;两直线平行,同旁内角互补;50;同旁内角互补,两直线平行.
解:OA∥BC,OB∥AC.
理由:∵∠1=50°,∠2=50°,
∴∠1=∠2(等量代换)
∴OB∥AC. ( 同位角相等,两直线平行),
∴∠3+∠ACB=180°,( 两直线平行,同旁内角互补),
∴∠ACB=50°,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥BC.( 同旁内角互补,两直线平行).
19.(1)见解析 (2)145°
(1)
证明:∵ABCD,
∴∠ABG=∠BGE,
∵BG平分∠ABE,
∴∠ABG=∠GBE,
∴∠BGE=∠GBE;
(2)
∵ABCD,
∴∠ABE=∠DEF=70°,
∴∠ABF=180° ∠ABE=110°,
∵BG平分∠ABE,
∴∠ABG= ∠ABE=35°,
∴∠FBG=∠ABF+∠ABG=110°+35°=145°.
答:∠FBG的度数为145°.
20.(1)见解析 (2)70°
(1)
解:∵,
∴∠1=∠CAE,
∵∠1+∠2=180°,
∴∠2+∠CAE=180°,
∴;
(2)
解:∵,∠C=35°,
∴∠BEF=∠C=35°,
∵EF平分∠AEB,
∴∠1=∠BEF=35°,
∴∠AEB=70°,
由(1)知,
∴∠BDG=∠AEB=70°.
21.(1)70°;
(2)∠EPF+(∠1+∠2) =360°,理由见解析;
(3)∠PGF的度数为140°.
(1)
解:过点P作PQ∥AB,
∴∠1+∠EPQ=180°,
∵∠1=135°,
∴∠EPQ=180°-∠1=45°,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠2+∠FPQ=180°,
∵∠2=155°,
∴∠FPQ=180°-∠2=25°,
∴∠EPF=∠EPQ+∠FPQ=70°;
故答案为:70°;
(2)
解:∠EPF+(∠1+∠2) =360°,理由如下:
过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠1+∠EPQ=180°,∠2+∠FPQ=180°,
即∠EPQ=180°-∠1,∠FPQ=180°-∠2,
∴∠EPF=∠EPQ+∠FPQ=360°-(∠1+∠2);
即∠EPF+(∠1+∠2) =360°;
(3)
解:过点P作PQ∥AB,过点G作GH∥AB,
∵AB∥CD,
∴PQ∥AB∥GH∥CD,
∴∠1+∠3=180°,∠4+∠5=180°,∠6+∠2=180°,
∴∠1+∠3+∠4+∠5+∠6+∠2=540°,
∵∠EPG=75°,
∴∠3+∠4=75°,
∵∠1+∠2=325°,
∴∠5+∠6=540°-(∠1+∠2)-(∠3+∠4)= 540°-325°-75°=140°.
∴∠PGF的度数为140°.
.
22.(1)证明见解析 (2)60° (3)70或290
(1)
证明:∵AB∥CD,
∴∠B=∠BCD.(两直线平行内错角相等),
同理可证,∠F=∠DCF.
∵∠BCF=∠BCD+∠DCF,
∴∠BCF=∠B+∠F.(等量代换)
(2)
解:由探究可知:∠MFN=∠AMF+∠CNF,∠MFN=115°,,
∴∠CNF=∠DNG=115°-55°=60°.
故答案为:60°.
(3)
如图3中,当点Q在直线GH的右侧时,
∵AB∥CD∥EF,
∴∠AGQ+∠GQC=180°,∠CQH+∠EHQ=180°,
即∠AGQ+∠GQH+∠EHQ=180°,
∴∠AGQ+∠EHQ=360°-70°=290°,
当点Q在直线GH的左侧时,由(1)的结论可得:
.
故答案为:70或290.
答案第1页,共2页
一、单选题
1.下列说法:①两直线平行,同旁内角互补;②内错角相等,两直线平行;③同位角相等,两直线平行;④垂直于同一条直线的两条直线平行,其中是平行线的性质的是( )
A.① B.②和③ C.④ D.①和④
2.如图,ABCD,AD⊥BD,∠1=53°,则∠2的大小是( )
A.53° B.50° C.37° D.23°
3.如图所示,把一个长方形纸片ABCD沿EF折叠后,点D,C分别落在点D,C位置,D'恰好在BC上,若∠,则∠ED'F等于( )
A.45° B.50° C.55° D.60°
4.生活中常见的探照灯、汽车大灯等灯具都与抛物线有关.如图,从光源P点照射到抛物线上的光线等反射以后沿着与直线平行的方向射出,若,,则的度数为( )°
A. B. C. D.
5.一把直尺与一块直角三角板按下图方式摆放,若,则( )
A.52° B.53° C.54° D.63°
6.如图,AB∥CD,AE∥CF,∠C=131°,则∠A=( )
A.39° B.41° C.49° D.51°
7.如图,若AB∥CD,CD∥EF,那么BCE=( )
A.180°-2+1 B.180°-1-2 C.2=21 D.1+2
8.一副三角板摆放如图所示,斜边FD与直角边AC相交于点E,点D在直角边BC上,且FDAB,∠B=30°,则∠ADB的度数是( )
A.95° B.105° C.115° D.125°
9.如果两个角的一边在同一直线上,另一边互相平行,则这两个角( )
A.相等 B.互补 C.互余 D.相等或互补
10.一学员在广场上练习驾驶汽车,两次拐弯后行驶的方向与原来的方向相同,这两次拐弯的角度可能是( ) .
A.第一次向左拐30°,第二次向右拐30°.
B.第一次向右拐50°,第二次向左拐130°.
C.第一次向左拐50°,第二次向左拐130°.
D.第一次向左拐50°,第二次向右拐130°.
11.如图,若要使与平行,则绕点至少旋转的度数是( )
A. B. C. D.
12.如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A.∠A+∠C+∠D+∠E=360° B.∠A+∠D=∠C+∠E
C.∠A﹣∠C+∠D+∠E=180° D.∠E﹣∠C+∠D﹣∠A=90°
二、填空题
13.如图,已知,,,则________度.
14.如图,有一块含30°角的直角三角板,两个顶点放在直尺的对边上,如果,______.
15.如图,ABCD,EFCD,平分,,则__.
16.如图,直线a与直线b平行,将三角板的直角顶点放在直线a上,若∠1=40°,到∠2=__°.
17.如图,已知AB∥CD,∠ABC=120°,∠1=27°,则直线CB和CE的夹角是_____°.
三、解答题
18.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,∠ACB的度数,并说明理由.
解:OA∥BC,OB∥AC.
理由:∵∠1=50°,∠2=50°,
∴∠1=∠2(等量代换)
∴OB∥AC. ( ),
∴∠3+∠ACB=180°,( ),
∴∠ACB= °,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥BC.( ).
19.如图,ABCD,点E在直线CD上,BG平分∠ABE交CD于点G.
(1)求证:∠BGE=∠GBE;
(2)若∠DEF=70°,求∠FBG的度数.
20.已知:如图,点D、E、F、G都在的边上,,且
(1)求证:;
(2)若EF平分,,求的度数.
21.如图①,直线AB∥CD,点E,F分别在直线AB,CD上.
(1)若∠1=135°,∠2=155°,试猜想∠P=______.
(2)在图①中探究∠1,∠P,∠2之间的数量关系,并证明你的结论.
(3)将图①变为图②,仍有AB∥CD,若∠1+∠2=325°,∠EPG=75°,求∠PGF的度数.
22.请回答下列各题.
(1)探究:如图1,AB∥CD∥EF,试说明∠BCF=∠B+∠F.
(2)应用:如图2,AB∥CD,点F在AB、CD之间,FE与AB交于点M,FG与CD交于点N.若∠EFG=115°,∠EMB=55°,则∠DNG的大小是多少?
(3)拓展:如图3,直线CD在直线AB、EF之间,且AB∥CD∥EF,点G、H分别在直线AB、EF上,点Q是直线CD上的一个动点,且不在直线GH上,连结QG、QH.若∠GQH=70°,则∠AGQ+∠EHQ=______度(请直接写出答案).
试卷第1页,共3页
参考答案:
1.A
解:①是平行线的性质,故符合题意;
②是平行线的判定,故不符合题意;
③是平行线的判定,故不符合题意;
④是平行线的判定,故不符合题意;
故选:A.
2.C
解:∵ABCD,∠1=53°,
∴∠BDC=180°﹣∠1=127°,
∵AD⊥BD,
∴∠ADB=90°,
∴∠2=∠BDC﹣∠ADB=37°.
故选:C.
3.B
解:由题意知AD∥BC,∠EFB=65°,
∴∠DEF=∠EFB=65°,∠ED'F=∠AED′
根据折叠变换的性质知∠D′EF=∠DEF=65°,
则∠AED′=180° ∠DEF ∠D′EF=50°,
∴∠ED'F=50°
故选B.
4.C
解:
故选C
5.B
解:如图,过三角板的直角顶点作直尺两边的平行线,
∵直尺的两边互相平行,
∴,,
∴,
∴,
故选B.
6.C
解:如图,
∵AB∥CD,∠C=131°,
∴∠1 =180°-∠C=49°(两直线平行,同旁内角互补),
∵AE∥CF,
∴∠A=∠C=49°(两直线平行,同位角相等).
故选:C.
7.A
解:∵AB∥CD,CD∥EF,
∴∠1=∠BCD,∠ECD+∠2=180°,
∴BCE=∠BCD+∠ECD=180°-2+1,
故选A.
8.B
解:由题意得∠ADF=45°,
∵,∠B=30°,
∴∠B+∠BDF=180°,
∴∠BDF=180°﹣∠B=150°,
∴∠ADB=∠BDF﹣∠ADF=105°.
故选:B
9.D
解:如图,当AE∥BD时,∠EAB与∠DBC符合题意,
∴∠EAB=∠DBC;
如图,当AE∥BD时,∠EAF与∠DBC符合题意,
∵∠EAB+∠EAF=180°,∠EAB=∠DBC,
∴∠DBC +∠EAF=180°,
故选D.
10.A
解:由第一次向左拐30°,第二次向右拐30°可得转完两次后相当于在原方向上转过了,和原来方向相同,故A正确;
第一次向右拐50°,第二次向左拐130°可得转完两次后相当于在原方向上左拐,故B错误;
第一次向左拐50°,第二次向左拐130°可得转完两次后相当于在原方向上右拐,故C错误;
第一次向左拐50°,第二次向右拐130°可得转完两次后相当于在原方向上右拐,故D错误;
综上所述,符合条件的是A.
故选:A.
11.A
解:如图,
∵l1∥l2,
∴∠AOB=∠OBC=42°,
∴80°-42°=38°,
即l1绕点O至少旋转38度才能与l2平行.
故选:A.
12.C
解:如图,过点C作CG∥AB,过点D作DH∥EF,
∴∠A=∠ACG,∠EDH=180°﹣∠E,
∵AB∥EF,
∴CG∥DH,
∴∠CDH=∠DCG,
∴∠ACD=∠ACG+∠CDH=∠A+∠CDE﹣(180°﹣∠E),
∴∠A﹣∠ACD+∠CDE+∠E=180°.
故选:C.
13.110
解:过E作一条直线
∵,,
∴,
∵,,
∴,
∴
又∵,
∴.
故答案为:110.
14.##35度
解:如图,根据题意可知,
∴,
∴.
故答案为:.
15.##147度
解:,
,
,
.
平分,
.
,
,
.
故答案为:.
16.50
解:如图
∵
∴∠2=∠3
∵∠1+∠3=90°,∠1=40°
∴
∴∠2=50°
故答案为;50.
17.93
解:∵AB∥CD
∴∠DCB=∠ABC=120°
又∵∠1=27°
∴∠BCE=∠DCB -∠1=93°
故答案为93.
18.同位角相等,两直线平行;两直线平行,同旁内角互补;50;同旁内角互补,两直线平行.
解:OA∥BC,OB∥AC.
理由:∵∠1=50°,∠2=50°,
∴∠1=∠2(等量代换)
∴OB∥AC. ( 同位角相等,两直线平行),
∴∠3+∠ACB=180°,( 两直线平行,同旁内角互补),
∴∠ACB=50°,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥BC.( 同旁内角互补,两直线平行).
19.(1)见解析 (2)145°
(1)
证明:∵ABCD,
∴∠ABG=∠BGE,
∵BG平分∠ABE,
∴∠ABG=∠GBE,
∴∠BGE=∠GBE;
(2)
∵ABCD,
∴∠ABE=∠DEF=70°,
∴∠ABF=180° ∠ABE=110°,
∵BG平分∠ABE,
∴∠ABG= ∠ABE=35°,
∴∠FBG=∠ABF+∠ABG=110°+35°=145°.
答:∠FBG的度数为145°.
20.(1)见解析 (2)70°
(1)
解:∵,
∴∠1=∠CAE,
∵∠1+∠2=180°,
∴∠2+∠CAE=180°,
∴;
(2)
解:∵,∠C=35°,
∴∠BEF=∠C=35°,
∵EF平分∠AEB,
∴∠1=∠BEF=35°,
∴∠AEB=70°,
由(1)知,
∴∠BDG=∠AEB=70°.
21.(1)70°;
(2)∠EPF+(∠1+∠2) =360°,理由见解析;
(3)∠PGF的度数为140°.
(1)
解:过点P作PQ∥AB,
∴∠1+∠EPQ=180°,
∵∠1=135°,
∴∠EPQ=180°-∠1=45°,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠2+∠FPQ=180°,
∵∠2=155°,
∴∠FPQ=180°-∠2=25°,
∴∠EPF=∠EPQ+∠FPQ=70°;
故答案为:70°;
(2)
解:∠EPF+(∠1+∠2) =360°,理由如下:
过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠1+∠EPQ=180°,∠2+∠FPQ=180°,
即∠EPQ=180°-∠1,∠FPQ=180°-∠2,
∴∠EPF=∠EPQ+∠FPQ=360°-(∠1+∠2);
即∠EPF+(∠1+∠2) =360°;
(3)
解:过点P作PQ∥AB,过点G作GH∥AB,
∵AB∥CD,
∴PQ∥AB∥GH∥CD,
∴∠1+∠3=180°,∠4+∠5=180°,∠6+∠2=180°,
∴∠1+∠3+∠4+∠5+∠6+∠2=540°,
∵∠EPG=75°,
∴∠3+∠4=75°,
∵∠1+∠2=325°,
∴∠5+∠6=540°-(∠1+∠2)-(∠3+∠4)= 540°-325°-75°=140°.
∴∠PGF的度数为140°.
.
22.(1)证明见解析 (2)60° (3)70或290
(1)
证明:∵AB∥CD,
∴∠B=∠BCD.(两直线平行内错角相等),
同理可证,∠F=∠DCF.
∵∠BCF=∠BCD+∠DCF,
∴∠BCF=∠B+∠F.(等量代换)
(2)
解:由探究可知:∠MFN=∠AMF+∠CNF,∠MFN=115°,,
∴∠CNF=∠DNG=115°-55°=60°.
故答案为:60°.
(3)
如图3中,当点Q在直线GH的右侧时,
∵AB∥CD∥EF,
∴∠AGQ+∠GQC=180°,∠CQH+∠EHQ=180°,
即∠AGQ+∠GQH+∠EHQ=180°,
∴∠AGQ+∠EHQ=360°-70°=290°,
当点Q在直线GH的左侧时,由(1)的结论可得:
.
故答案为:70或290.
答案第1页,共2页
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
