2021-2022学年沪科版数学九年级下册 24.3圆周角 课时练习(word版 含解析)
文档属性
| 名称 | 2021-2022学年沪科版数学九年级下册 24.3圆周角 课时练习(word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 598.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 00:00:00 | ||
图片预览

文档简介
圆周角
一、单选题
1.下列图形中,为圆心角的是( )
A. B.
C. D.
2.如图,⊙O的两条弦AB⊥CD,已知∠ADC=35°,则∠BAD的度数为( )
A.55° B.70° C.110° D.130°
3.如图,AB是⊙O的直径,点C,D在⊙O上.若∠ABC=60°,则∠D的度数为( )
A.25° B.30° C.35° D.40°
4.如图,是上一个定点,将直角三角板的角顶点与点重合,两边与相交,设交点为,,绕点顺时针旋转三角板,直至其中一个交点与点重合时停止旋转,设,旋转角为,如图所示能反映与关系的为( )
A. B.
C. D.
5.如图,在中,CD为的直径,,,,则弦( )
A. B. C. D.
6.如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为弧BC的中点,E是直径AB上一动点,则CE+DE最小值为( )
A.1 B. C. D.2
7.如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠ACE=20°,则∠BDE的度数为( )
A.90° B.100° C.110° D.120°
8.如图,AB是⊙O的直径,CD是弦,若∠BCD=36°,则∠ABD等于( )
A.36° B.54° C.64° D.72°
9.如图,AB是⊙O的直径,若AC=4,∠D=60°,则BC长等于( )
A.8 B.10 C. D.
10.如图,在平面直角坐标系中,⊙P经过原点O,并且分别与x轴、y轴相交于A、B两点,已知A(﹣3,0)、B(0,4),则⊙P的半径为( )
A.5 B.4 C.3 D.2.5
11.如图所示,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的余弦值为( )
A. B. C. D.
12.如图,在的正方形网格中,经过格点,,,点是上任意一点,连接,,则的值为( )
A. B. C. D.
二、填空题
13.如图,、、、是上的四个点,,交于点,若,,则_______.
14.如图,AB是⊙O的一条直径,点C是⊙O上的一点(不与点A,点B重合),分别连接AC,BC,半径OE⊥AC于点D,若BC=DE=2,则AC=______.
15.如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,E为线段CD上一个动点,连接OE,则OE的最小值为___.
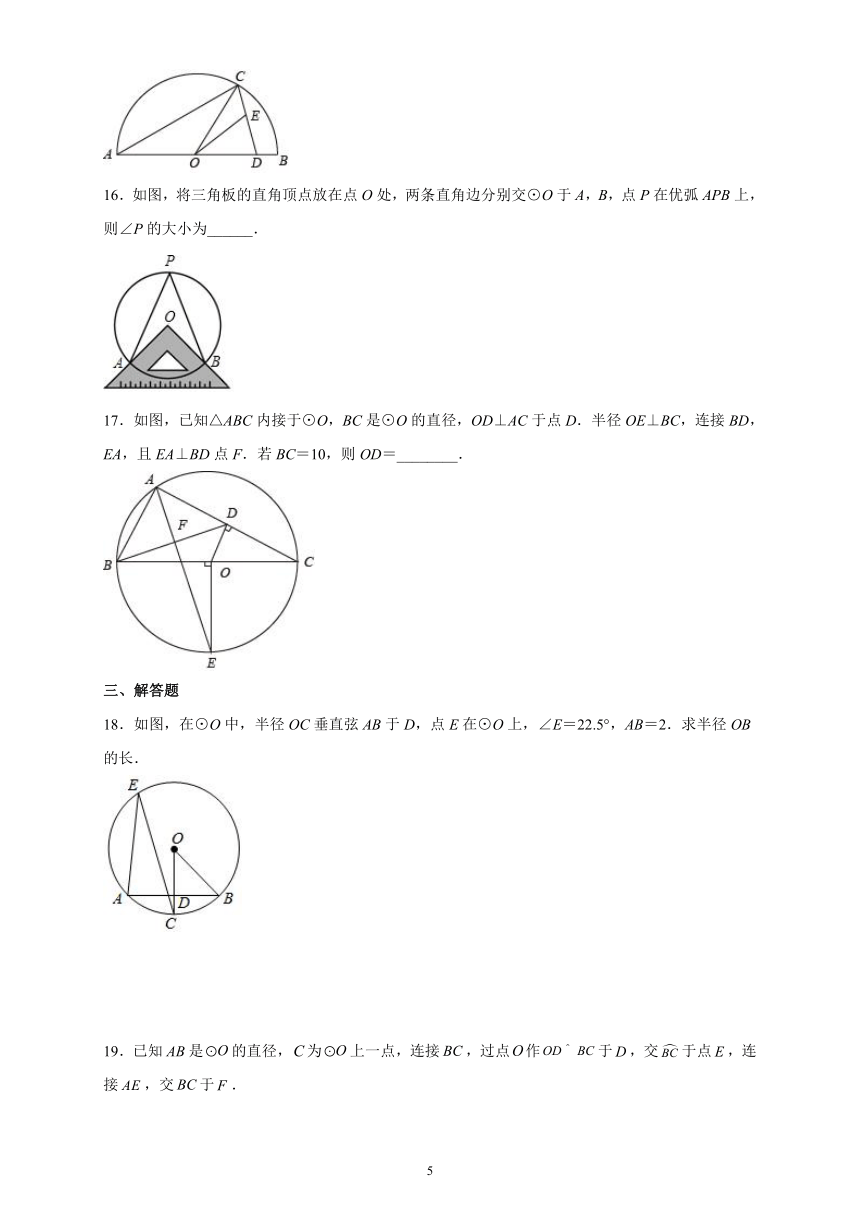
16.如图,将三角板的直角顶点放在点O处,两条直角边分别交⊙O于A,B,点P在优弧APB上,则∠P的大小为______.
17.如图,已知△ABC内接于⊙O,BC是⊙O的直径,OD⊥AC于点D.半径OE⊥BC,连接BD,EA,且EA⊥BD点F.若BC=10,则OD=________.
三、解答题
18.如图,在⊙O中,半径OC垂直弦AB于D,点E在⊙O上,∠E=22.5°,AB=2.求半径OB的长.
19.已知是的直径,为上一点,连接,过点作于,交于点,连接,交于.
(1)如图1,求证:.
(2)如图2,连接,若,,求的长.
20.如图,△ABC为⊙O的内接三角形,AD⊥BC,垂足为D,直径AE平分∠BAD,交BC于点F,连结BE.
(1)求证:∠AEB=∠AFD.
(2)若AB=10,BF=5,求AD的长.
(3)若点G为AB中点,连结DG,若点O在DG上,求BF:FC的值.
21.圆内接四边形ABCD,AB为的直径.
(1)如图1,若D为弧AB中点,.
①求的度数;
②求四边形ABCD面积的最大值.
(2)如图2,对角线AC,BD交于点E,连结OE并延长交CD于点F,若,求AB的长.
试卷第1页,共3页
参考答案:
1.C
解:根据圆心角定义可知:
A.顶点不是圆心,所以A选项不符合题意;
B.顶点在圆上,∠AOB圆周角,所以B选项不符合题意;
C.∠AOB顶点是圆心,两边与圆相交,所以C选项符合题意;
D.顶点在圆上,∠AOB圆周角,所以D选项不符合题意.
故选:C.
2.A
解:∵AB⊥CD,
∴∠ADC+∠BAD=90°,
∵∠ADC=35°,
∴∠BAD=90°﹣35°=55°,
故选:A.
3.B
解:∵AB是直径,
∴∠ACB=90°,
∵∠ABC=60°,
∴∠A=90°﹣∠ABC=30°,
∴∠D=∠A=30°,
故选:B.
4.A
解:依题意可知∠BMA是圆周角,弦AB为∠BMA所对的弦,
当绕点顺时针旋转三角板时,∠BMA的大小不变,故弦AB长度不变,即y不随的变化而变化,
故选A.
5.D
解:连接BD,
∵CD为⊙O的直径,CD⊥AB,
∴AB=2BF,,
∵∠AEC=60°,
∴∠ODB=∠AEC=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴OB=OD=4,
∴OF=OD=2,
∴BF=,
∴AB=2BF=,
故选:D.
6.B
解:作点D关于AB的对称点为D′,连接OC,OD,OD′,CD′,交AB于点E,
∴DE=D′E,
∴CE+DE=CE+D′E=CD′,
∵∠CAB=30°,
∴∠COB=2∠CAB=60°,
∵D为的中点,
∴,
∵,
∴,
∴∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∵AB=2,
∴OC=OD′=1,
∴CD′=,
∴CE+DE最小值为:,
故选:B.
7.C
解:连接,
为的直径,
,
,
,
,
故选:C.
8.B
解:∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∵∠DAB=∠BCD=36°,
∴∠ABD=90°-36°=54°.
故选:B.
9.D
解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=∠D=60°,
∴∠ABC=90°-∠A=30°,
∵AC=4,
∴AB=2AC=8.
∴BC=.
故选:D.
10.D
解:连接AB,如下图所示:
∵∠AOB=90°,A、B为圆P上两点,
∴AB为圆P的直径,
在Rt△ABO中,由勾股定理可知:AB =AO +BO =9+16=25,
∴AB=5,
∴圆P的半径为2.5,
故选:D.
11.C
解:设⊙A交x轴于另一点D,连接CD,作图如下:
∵
∴CD是直径
∴CD=10
∵
∴OC=5
在中,, OC=5, CD=10
由勾股定理得:
即:
∵
∴
∵
∴∠OBC=∠ODC,
∴在中,
故选:C
12.C
解:连接AC,
∵经过格点,,,
∴∠ABC=90°,
∴AC是的直径,
在Rt△ABC中,AC=
∴
故选:C.
13.
解:,
,
,
,
,
.
,即,
.
故答案为:.
14.4
解:∵OE⊥AC,
∴AD=CD,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴,
∴OD为△ABC的中位线,
∴OD=BC=1,
∵DE=2,
∴OE=3,
∴AB=6,
在Rt△ABC中,AC===.
故答案为:.
15.
解:过O点作OF⊥CD于F,如图,
∵AC=AD,
∴,
∵∠BOC=2∠A=60°,
∴∠OCD=180° ∠DOC ∠ODC=180° 60° 75°=45°,
∴△COF为等腰直角三角形,
∴,
∴OE的最小值为.
故答案为:.
16.45°##45度
解:∵∠AOB与∠APB为所对的圆心角和圆周角,
∴∠APB=∠AOB=×90°=45°.
故答案为:45°.
17.
解:∵OD⊥AC于点D
∴
BC是⊙O的直径,
OE⊥BC,
EA⊥BD
设,则
在中,
,则
18.
解:半径弦于点,
,
,
,
是等腰直角三角形,
,
,
19.(1)见解析 (2)
(1)
证明:如图1中,
是直径,
,
,
,
,
,
,
,
;
(2)
解:如图2中,
,,
,
,
,
,
,
,
,
,
,
,
,
,,
.
20.(1)证明见解析 (2)6 (3):2
(1)
∵直径AE平分∠BAD,
∴∠BAE=∠DAE,∠ABE=90°,
∴∠BAE+∠AEB=90°,
∵AD⊥BC,
∴∠DAE+∠AFD=90°,
∴∠AEB=∠AFD.
(2)
∵∠AEB=∠AFD,∠AFD=∠BFE,
∴∠BFE=∠BEF,
∴BE=BF,
∵∠BAE=∠DAF,∠ABE=∠ADF,
∴△ABE∽△ADF,
∵AB=10,BF=5,
∴,
设DF=x,则AD=2x,
∴在Rt△ABD中,AB2=BD2+AD2,即102=(5+x)2+(2x)2,
解得:x=3,(负值舍去)
∴AD=2x=6.
(3)
∵点G为AB中点,点O在DG上,
∴OG是△ABE的中位线,
∴OG//BE,OG=BE,
∵∠ABE=90°,
∴DG⊥AB,∠AOG=∠AEB=∠AFD,
∴OD=DF,△ABD是等腰直角三角形,
∵∠AEB和∠ACB是所对的圆周角,
∴∠AEB=∠ACB,
∴∠ACB=∠AFC,
∴AC=AF,
∵AD⊥CF,
∴DF=CD,
设BF=a,DF=b,
∴,
∴,
∴BF:FC=a:2b=:2.
21.(1)①;②的最大值为
(2)
(1)
解:①∵AB为直径,D为弧AB中点,
∴,
∴,
②连结BD,OC交于点E,当四边形ABCD面积最大时,
即面积最大,
∴只需C到BD的距离最大,
当时,CE最大,
∵,
∴,
,
∴,
∴的最大值为,
(2)
解:直线OF交圆于点M,N,
过F作交直线BD,AC于点P,Q,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,,
∴,
设半径为r,
∴,
∴,
.
答案第1页,共2页
一、单选题
1.下列图形中,为圆心角的是( )
A. B.
C. D.
2.如图,⊙O的两条弦AB⊥CD,已知∠ADC=35°,则∠BAD的度数为( )
A.55° B.70° C.110° D.130°
3.如图,AB是⊙O的直径,点C,D在⊙O上.若∠ABC=60°,则∠D的度数为( )
A.25° B.30° C.35° D.40°
4.如图,是上一个定点,将直角三角板的角顶点与点重合,两边与相交,设交点为,,绕点顺时针旋转三角板,直至其中一个交点与点重合时停止旋转,设,旋转角为,如图所示能反映与关系的为( )
A. B.
C. D.
5.如图,在中,CD为的直径,,,,则弦( )
A. B. C. D.
6.如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为弧BC的中点,E是直径AB上一动点,则CE+DE最小值为( )
A.1 B. C. D.2
7.如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠ACE=20°,则∠BDE的度数为( )
A.90° B.100° C.110° D.120°
8.如图,AB是⊙O的直径,CD是弦,若∠BCD=36°,则∠ABD等于( )
A.36° B.54° C.64° D.72°
9.如图,AB是⊙O的直径,若AC=4,∠D=60°,则BC长等于( )
A.8 B.10 C. D.
10.如图,在平面直角坐标系中,⊙P经过原点O,并且分别与x轴、y轴相交于A、B两点,已知A(﹣3,0)、B(0,4),则⊙P的半径为( )
A.5 B.4 C.3 D.2.5
11.如图所示,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的余弦值为( )
A. B. C. D.
12.如图,在的正方形网格中,经过格点,,,点是上任意一点,连接,,则的值为( )
A. B. C. D.
二、填空题
13.如图,、、、是上的四个点,,交于点,若,,则_______.
14.如图,AB是⊙O的一条直径,点C是⊙O上的一点(不与点A,点B重合),分别连接AC,BC,半径OE⊥AC于点D,若BC=DE=2,则AC=______.
15.如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,E为线段CD上一个动点,连接OE,则OE的最小值为___.
16.如图,将三角板的直角顶点放在点O处,两条直角边分别交⊙O于A,B,点P在优弧APB上,则∠P的大小为______.
17.如图,已知△ABC内接于⊙O,BC是⊙O的直径,OD⊥AC于点D.半径OE⊥BC,连接BD,EA,且EA⊥BD点F.若BC=10,则OD=________.
三、解答题
18.如图,在⊙O中,半径OC垂直弦AB于D,点E在⊙O上,∠E=22.5°,AB=2.求半径OB的长.
19.已知是的直径,为上一点,连接,过点作于,交于点,连接,交于.
(1)如图1,求证:.
(2)如图2,连接,若,,求的长.
20.如图,△ABC为⊙O的内接三角形,AD⊥BC,垂足为D,直径AE平分∠BAD,交BC于点F,连结BE.
(1)求证:∠AEB=∠AFD.
(2)若AB=10,BF=5,求AD的长.
(3)若点G为AB中点,连结DG,若点O在DG上,求BF:FC的值.
21.圆内接四边形ABCD,AB为的直径.
(1)如图1,若D为弧AB中点,.
①求的度数;
②求四边形ABCD面积的最大值.
(2)如图2,对角线AC,BD交于点E,连结OE并延长交CD于点F,若,求AB的长.
试卷第1页,共3页
参考答案:
1.C
解:根据圆心角定义可知:
A.顶点不是圆心,所以A选项不符合题意;
B.顶点在圆上,∠AOB圆周角,所以B选项不符合题意;
C.∠AOB顶点是圆心,两边与圆相交,所以C选项符合题意;
D.顶点在圆上,∠AOB圆周角,所以D选项不符合题意.
故选:C.
2.A
解:∵AB⊥CD,
∴∠ADC+∠BAD=90°,
∵∠ADC=35°,
∴∠BAD=90°﹣35°=55°,
故选:A.
3.B
解:∵AB是直径,
∴∠ACB=90°,
∵∠ABC=60°,
∴∠A=90°﹣∠ABC=30°,
∴∠D=∠A=30°,
故选:B.
4.A
解:依题意可知∠BMA是圆周角,弦AB为∠BMA所对的弦,
当绕点顺时针旋转三角板时,∠BMA的大小不变,故弦AB长度不变,即y不随的变化而变化,
故选A.
5.D
解:连接BD,
∵CD为⊙O的直径,CD⊥AB,
∴AB=2BF,,
∵∠AEC=60°,
∴∠ODB=∠AEC=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴OB=OD=4,
∴OF=OD=2,
∴BF=,
∴AB=2BF=,
故选:D.
6.B
解:作点D关于AB的对称点为D′,连接OC,OD,OD′,CD′,交AB于点E,
∴DE=D′E,
∴CE+DE=CE+D′E=CD′,
∵∠CAB=30°,
∴∠COB=2∠CAB=60°,
∵D为的中点,
∴,
∵,
∴,
∴∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∵AB=2,
∴OC=OD′=1,
∴CD′=,
∴CE+DE最小值为:,
故选:B.
7.C
解:连接,
为的直径,
,
,
,
,
故选:C.
8.B
解:∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∵∠DAB=∠BCD=36°,
∴∠ABD=90°-36°=54°.
故选:B.
9.D
解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=∠D=60°,
∴∠ABC=90°-∠A=30°,
∵AC=4,
∴AB=2AC=8.
∴BC=.
故选:D.
10.D
解:连接AB,如下图所示:
∵∠AOB=90°,A、B为圆P上两点,
∴AB为圆P的直径,
在Rt△ABO中,由勾股定理可知:AB =AO +BO =9+16=25,
∴AB=5,
∴圆P的半径为2.5,
故选:D.
11.C
解:设⊙A交x轴于另一点D,连接CD,作图如下:
∵
∴CD是直径
∴CD=10
∵
∴OC=5
在中,, OC=5, CD=10
由勾股定理得:
即:
∵
∴
∵
∴∠OBC=∠ODC,
∴在中,
故选:C
12.C
解:连接AC,
∵经过格点,,,
∴∠ABC=90°,
∴AC是的直径,
在Rt△ABC中,AC=
∴
故选:C.
13.
解:,
,
,
,
,
.
,即,
.
故答案为:.
14.4
解:∵OE⊥AC,
∴AD=CD,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴,
∴OD为△ABC的中位线,
∴OD=BC=1,
∵DE=2,
∴OE=3,
∴AB=6,
在Rt△ABC中,AC===.
故答案为:.
15.
解:过O点作OF⊥CD于F,如图,
∵AC=AD,
∴,
∵∠BOC=2∠A=60°,
∴∠OCD=180° ∠DOC ∠ODC=180° 60° 75°=45°,
∴△COF为等腰直角三角形,
∴,
∴OE的最小值为.
故答案为:.
16.45°##45度
解:∵∠AOB与∠APB为所对的圆心角和圆周角,
∴∠APB=∠AOB=×90°=45°.
故答案为:45°.
17.
解:∵OD⊥AC于点D
∴
BC是⊙O的直径,
OE⊥BC,
EA⊥BD
设,则
在中,
,则
18.
解:半径弦于点,
,
,
,
是等腰直角三角形,
,
,
19.(1)见解析 (2)
(1)
证明:如图1中,
是直径,
,
,
,
,
,
,
,
;
(2)
解:如图2中,
,,
,
,
,
,
,
,
,
,
,
,
,
,,
.
20.(1)证明见解析 (2)6 (3):2
(1)
∵直径AE平分∠BAD,
∴∠BAE=∠DAE,∠ABE=90°,
∴∠BAE+∠AEB=90°,
∵AD⊥BC,
∴∠DAE+∠AFD=90°,
∴∠AEB=∠AFD.
(2)
∵∠AEB=∠AFD,∠AFD=∠BFE,
∴∠BFE=∠BEF,
∴BE=BF,
∵∠BAE=∠DAF,∠ABE=∠ADF,
∴△ABE∽△ADF,
∵AB=10,BF=5,
∴,
设DF=x,则AD=2x,
∴在Rt△ABD中,AB2=BD2+AD2,即102=(5+x)2+(2x)2,
解得:x=3,(负值舍去)
∴AD=2x=6.
(3)
∵点G为AB中点,点O在DG上,
∴OG是△ABE的中位线,
∴OG//BE,OG=BE,
∵∠ABE=90°,
∴DG⊥AB,∠AOG=∠AEB=∠AFD,
∴OD=DF,△ABD是等腰直角三角形,
∵∠AEB和∠ACB是所对的圆周角,
∴∠AEB=∠ACB,
∴∠ACB=∠AFC,
∴AC=AF,
∵AD⊥CF,
∴DF=CD,
设BF=a,DF=b,
∴,
∴,
∴BF:FC=a:2b=:2.
21.(1)①;②的最大值为
(2)
(1)
解:①∵AB为直径,D为弧AB中点,
∴,
∴,
②连结BD,OC交于点E,当四边形ABCD面积最大时,
即面积最大,
∴只需C到BD的距离最大,
当时,CE最大,
∵,
∴,
,
∴,
∴的最大值为,
(2)
解:直线OF交圆于点M,N,
过F作交直线BD,AC于点P,Q,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,,
∴,
设半径为r,
∴,
∴,
.
答案第1页,共2页
