湘教版数学九年级下册 2.5.1圆的切线的判定 课件 (共13张PPT)
文档属性
| 名称 | 湘教版数学九年级下册 2.5.1圆的切线的判定 课件 (共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 198.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 10:59:17 | ||
图片预览





文档简介
(共13张PPT)
2.5.1 圆的切线(一)
复习引入:
1、直线和圆有哪几种位置关系?
2、直线和圆的位置关系的判定方法?
1、理解并掌握切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
学习目标
2、掌握圆的切线的两种证明方法。
自学指导:
阅读教材73-75,完成探究部分,理解切线的判定定理和判定方法:
1、判定定理:_____________.
2、判定方法(1)经过圆上一点,只须证_________.简称连______证_____。
(2)没有明确与圆相交,那么要证明圆心到直线的距离等于_____。简称作______证______。
1、下列命题中正确的是( )
A.与圆有公共点的直线是圆的切线
B.经过半径外端点且与这条半径垂直的直线是圆的直径
C.垂直于圆的半径的直线是圆的切线
D.到圆心的距离等于圆的半径的直线是圆的切线
D
2、如L是⊙O的切线,要判定AB⊥L,还需要添加的条件是( )
A.AB经过圆心O B.AB是直径
C.AB是直径,B是切点 D.AB是直线,B是切点
自学检测:
C
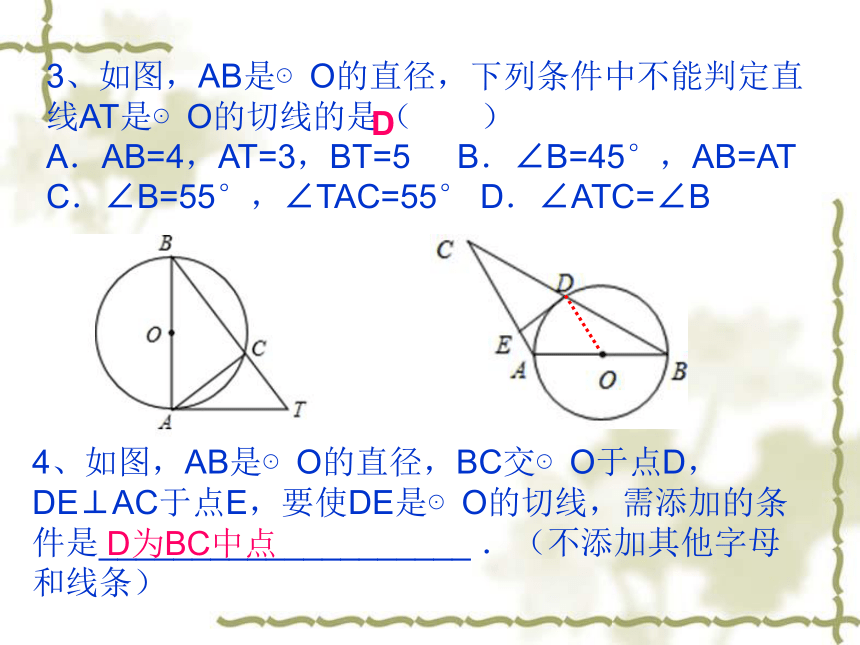
3、如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是( )
A.AB=4,AT=3,BT=5 B.∠B=45°,AB=AT
C.∠B=55°,∠TAC=55° D.∠ATC=∠B
4、如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,需添加的条件是____________________ .(不添加其他字母和线条)
D为BC中点
D
一展身手:
连半径,证垂直
1、已知:如图,AB是⊙O的直径,P为⊙O外一点,PA⊥AB,弦BC∥OP
求证:PC是⊙O的切线.
证明:如图,连接OC;
∵BC∥OP,
∴∠B=∠POA,∠BCO=∠COP,
∵OB=OC,
∴∠B=∠OCB,
∴∠COP=∠AOP;
∵OC=OA,OP=OP,
∴△PCO≌△PAO,
∴∠OCP=∠OAP=90°,
∴PC是⊙O的切线.
2、如图,△ABC为等腰三角形,AB=AC,O是底边BC的中点,⊙O与AB相切于点D,求证AC与⊙O相切。
证明:连结OD,过点O作OE⊥AC于E点。
∵AB切⊙O于D ∴OD⊥AB
∴∠ODB=∠OEC=90°
又∵O是BC的中点 ∴OB=OC
∵AB=AC ∴∠B=∠C
∴△OBE≌△OCE
∴OE=OD,即OE是⊙O的半径
∴AC与⊙O相切科
E
作垂直;证半径
挑战自我:
1、已知:如图,△ABC内接于⊙O,AB为直径,过点A作直线EF,要使得EF是⊙O的切线,还需添加的条件是(只需写出三种):①__________________ 或②_______________ 或③__________________.
OA⊥EF
∠FAC=∠B
∠BAC+∠FAC=90°
并选其中一种加以证明。
在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.
(1)求证:AC与⊙O相切.
(2)若BC=6,AB=12,求⊙O的面积.
课堂小结
谈谈你这节课的收获?
要证切线看情况:公共点已知与未知,
1、圆的切线的判定方法?
2、圆的切线的证明方法?
已知公共点连半径证垂直,
未知公共点作垂直证半径。
当堂训练
1、已知:如图,AC,BD与⊙O切于A、B,且AC∥BD,若∠COD=900. 求证:CD是⊙O的切线.
A
C
B
D
0
2、如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的直线,垂足为D,且AC平分∠BAD.
(1)求证:CD是⊙O的切线;
如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD.
(1)若AB=2,OD=3,求BC的长;
(2)若作直线CD,试说明直线CD是⊙O的切线.
2.5.1 圆的切线(一)
复习引入:
1、直线和圆有哪几种位置关系?
2、直线和圆的位置关系的判定方法?
1、理解并掌握切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
学习目标
2、掌握圆的切线的两种证明方法。
自学指导:
阅读教材73-75,完成探究部分,理解切线的判定定理和判定方法:
1、判定定理:_____________.
2、判定方法(1)经过圆上一点,只须证_________.简称连______证_____。
(2)没有明确与圆相交,那么要证明圆心到直线的距离等于_____。简称作______证______。
1、下列命题中正确的是( )
A.与圆有公共点的直线是圆的切线
B.经过半径外端点且与这条半径垂直的直线是圆的直径
C.垂直于圆的半径的直线是圆的切线
D.到圆心的距离等于圆的半径的直线是圆的切线
D
2、如L是⊙O的切线,要判定AB⊥L,还需要添加的条件是( )
A.AB经过圆心O B.AB是直径
C.AB是直径,B是切点 D.AB是直线,B是切点
自学检测:
C
3、如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是( )
A.AB=4,AT=3,BT=5 B.∠B=45°,AB=AT
C.∠B=55°,∠TAC=55° D.∠ATC=∠B
4、如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,需添加的条件是____________________ .(不添加其他字母和线条)
D为BC中点
D
一展身手:
连半径,证垂直
1、已知:如图,AB是⊙O的直径,P为⊙O外一点,PA⊥AB,弦BC∥OP
求证:PC是⊙O的切线.
证明:如图,连接OC;
∵BC∥OP,
∴∠B=∠POA,∠BCO=∠COP,
∵OB=OC,
∴∠B=∠OCB,
∴∠COP=∠AOP;
∵OC=OA,OP=OP,
∴△PCO≌△PAO,
∴∠OCP=∠OAP=90°,
∴PC是⊙O的切线.
2、如图,△ABC为等腰三角形,AB=AC,O是底边BC的中点,⊙O与AB相切于点D,求证AC与⊙O相切。
证明:连结OD,过点O作OE⊥AC于E点。
∵AB切⊙O于D ∴OD⊥AB
∴∠ODB=∠OEC=90°
又∵O是BC的中点 ∴OB=OC
∵AB=AC ∴∠B=∠C
∴△OBE≌△OCE
∴OE=OD,即OE是⊙O的半径
∴AC与⊙O相切科
E
作垂直;证半径
挑战自我:
1、已知:如图,△ABC内接于⊙O,AB为直径,过点A作直线EF,要使得EF是⊙O的切线,还需添加的条件是(只需写出三种):①__________________ 或②_______________ 或③__________________.
OA⊥EF
∠FAC=∠B
∠BAC+∠FAC=90°
并选其中一种加以证明。
在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.
(1)求证:AC与⊙O相切.
(2)若BC=6,AB=12,求⊙O的面积.
课堂小结
谈谈你这节课的收获?
要证切线看情况:公共点已知与未知,
1、圆的切线的判定方法?
2、圆的切线的证明方法?
已知公共点连半径证垂直,
未知公共点作垂直证半径。
当堂训练
1、已知:如图,AC,BD与⊙O切于A、B,且AC∥BD,若∠COD=900. 求证:CD是⊙O的切线.
A
C
B
D
0
2、如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的直线,垂足为D,且AC平分∠BAD.
(1)求证:CD是⊙O的切线;
如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD.
(1)若AB=2,OD=3,求BC的长;
(2)若作直线CD,试说明直线CD是⊙O的切线.
