湘教版数学九年级下册 2.6扇形面积课件 (共27张PPT)
文档属性
| 名称 | 湘教版数学九年级下册 2.6扇形面积课件 (共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 456.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
扇形面积
一把美丽的扇子你会计算当中纸片的面积吗?
创设情境
学习目标:
1、了解扇形面积公式的推导.
2、学会运用扇形面积公式进行简单的计算与运用.
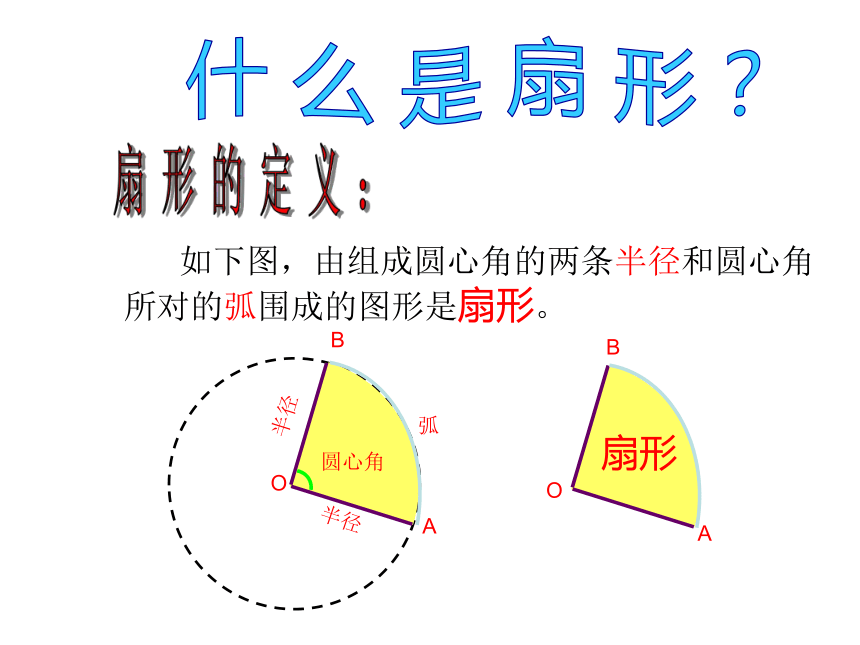
什 么 是 扇 形 ?
扇 形 的 定 义 :
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
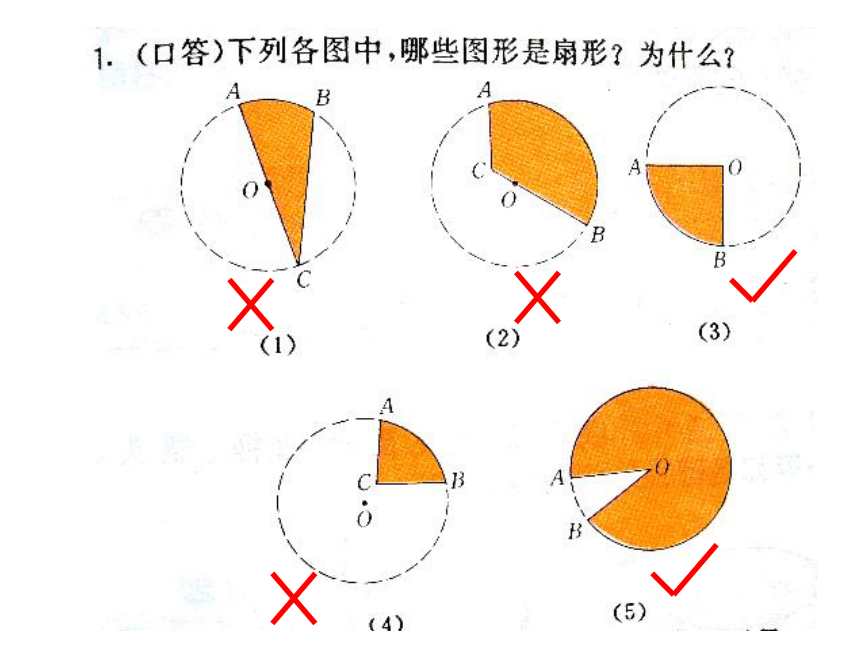
如 何 求 扇 形 的 面 积 ?
设 问 :
扇形面积的大小到底和哪些因素有关呢?
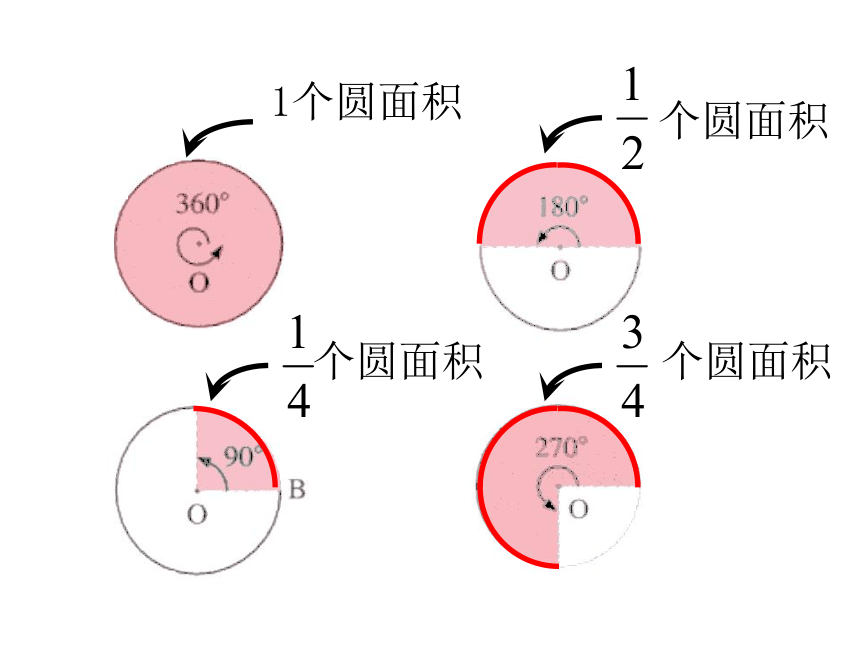
想 一 想 :
1. 圆心角是3600的扇形面积是多少?
2. 圆心角是1800的扇形面积是多少?
3. 圆心角是900的扇形面积是多少?
4. 圆心角是2700的扇形面积是多少?
1个圆面积
个圆面积
个圆面积
个圆面积
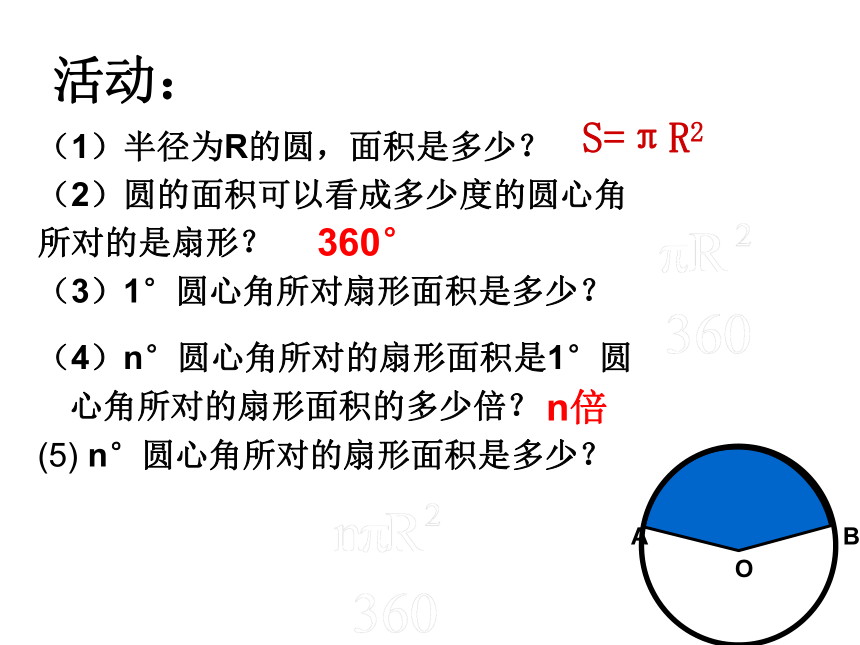
活动:
(1)半径为R的圆,面积是多少?
(2)圆的面积可以看成多少度的圆心角
所对的是扇形?
(3)1°圆心角所对扇形面积是多少?
(4)n°圆心角所对的扇形面积是1°圆心角所对的扇形面积的多少倍?
(5) n°圆心角所对的扇形面积是多少?
A
B
O
360°
n倍
S=πR2
若设⊙O半径为R,圆心角为n°的扇形的面积为
在应用扇形面积公式 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位 的;公式中S、n、R三个量中已知两量可求第三量.
扇形面积公式
注意:
360
R
n
2
p
=
扇形
S
弧长公式与扇形面积公式的区别与联系
弧长与圆的周长有关,扇形的面积与圆的面积有关。因此,计算弧长是 ;
而计算扇形的面积时是 。
C圆
360
n
S圆
360
n
小组活动
根据扇形的面积计算公式为
S、n、R三个量中已知两量可求第三量.请
各小组拟出一题写出已知求解过程.
回顾问题
2、一把美丽的扇子你会计算当中纸片的面积吗?
如图:纸扇中OC=8
AC=12,角AOB
= 120°,求纸扇
中纸片ABCD的面积.
O
C
A
D
B
思考:扇形的面积公式与弧长公式有联系吗?
R
随堂训练
1、已知扇形的圆心角为120°,半径为2,则这个
扇形的面积S扇形=____.
2、已知扇形面积为 ,圆心角为60°,则这个
扇形的半径R=____.
3、已知半径为2cm的扇形,其弧长为 ,
则这个扇形的面积是_________.
随堂训练
4、(07·内江)如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为120°,OC
长为8cm,CA长为12
cm,则贴纸部分的面
积为( )
A. B.
C. D.
5.课本P114【习题24.4】第1题(1)、(2)
例1.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。
0
B
A
C
D
S弓形= S扇形- S△
例题点评
练习:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。
0
A
B
D
C
E
变式训练
S弓形= S扇形+S△
感悟:
①当弓形面积小于半圆时
S弓形= S扇形-S△
②当弓形面积大于半圆时
S弓形= S扇形+S△
效果检测
3. 已知等边三角形ABC的边长为a,分别以A、B、C为圆心,以 为半径的圆相切于点D、 E、F,求图中阴影部分的面积S.
A.
B.
C.
D.
1.(08·眉山)如图,等边△ABC
的边长为12cm,
切
边BC于D点,
则图中阴影部分的
内切⊙O
面积为( )
C
当堂训练
当堂训练
O
2.(08·潍坊)如图,正六边形内接于圆O,
圆O
的半径为10,则圆中阴影部分的面积为______.
6、(2009年长春)如图,方格纸中4个
小正方形的边长均为1,则图中阴影部分三个
小扇形的面积和为 (结果保留
).
随堂训练
2. (2006,武汉)如图,⊙A、⊙B、⊙C、⊙D相互外离,它们的半径都是1,顺次连接四个圆心得到四边形ABCD,则图形中四个扇形(空白部分)的面积之和是___________.
点击中考
3.(2007,山东)如图所示,分别以n边形的顶点为圆心,以单位1为半径画圆,则图中阴影部分的面积之和为 个平方单位.
点击中考
6. (08·鄂州)如图,Rt△ABC中,∠C=90°, ∠A=30°,BC=2,O、H分别为AB、AC
的中点,将
△ABC顺时针旋转120°到△A1BC1的位置,则整
个旋转过程中线段OH所扫过的面积为( )
B.
C. D.
A
H
B
O
C
H1
O1
A1
C1
C
当堂训练
小 结 :
2. 扇形面积公式与弧长公式的区别:
S扇形= S圆
360
n
l弧= C圆
360
n
1. 扇形的面积大小与哪些因素有关?
(1)与圆心角的大小有关
(2)与半径的长短有关
3. 扇形面积单位与弧长单位的区别:
(1)扇形面积单位有平方的
(2)弧长单位没有平方的
颗粒归仓
1.弧长公式:
2.扇形面积公式:
注意:
(1)两个公式的联系和区别;
(2)两个公式的逆向应用。
努力是半径R,恒心是圆心角n,学习上的收获好比扇形面积S,只有你努力与恒心不断的变大变长你的学习才能有更大的收获面积。
教师寄语
作业:P56
扇形面积
一把美丽的扇子你会计算当中纸片的面积吗?
创设情境
学习目标:
1、了解扇形面积公式的推导.
2、学会运用扇形面积公式进行简单的计算与运用.
什 么 是 扇 形 ?
扇 形 的 定 义 :
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
如 何 求 扇 形 的 面 积 ?
设 问 :
扇形面积的大小到底和哪些因素有关呢?
想 一 想 :
1. 圆心角是3600的扇形面积是多少?
2. 圆心角是1800的扇形面积是多少?
3. 圆心角是900的扇形面积是多少?
4. 圆心角是2700的扇形面积是多少?
1个圆面积
个圆面积
个圆面积
个圆面积
活动:
(1)半径为R的圆,面积是多少?
(2)圆的面积可以看成多少度的圆心角
所对的是扇形?
(3)1°圆心角所对扇形面积是多少?
(4)n°圆心角所对的扇形面积是1°圆心角所对的扇形面积的多少倍?
(5) n°圆心角所对的扇形面积是多少?
A
B
O
360°
n倍
S=πR2
若设⊙O半径为R,圆心角为n°的扇形的面积为
在应用扇形面积公式 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位 的;公式中S、n、R三个量中已知两量可求第三量.
扇形面积公式
注意:
360
R
n
2
p
=
扇形
S
弧长公式与扇形面积公式的区别与联系
弧长与圆的周长有关,扇形的面积与圆的面积有关。因此,计算弧长是 ;
而计算扇形的面积时是 。
C圆
360
n
S圆
360
n
小组活动
根据扇形的面积计算公式为
S、n、R三个量中已知两量可求第三量.请
各小组拟出一题写出已知求解过程.
回顾问题
2、一把美丽的扇子你会计算当中纸片的面积吗?
如图:纸扇中OC=8
AC=12,角AOB
= 120°,求纸扇
中纸片ABCD的面积.
O
C
A
D
B
思考:扇形的面积公式与弧长公式有联系吗?
R
随堂训练
1、已知扇形的圆心角为120°,半径为2,则这个
扇形的面积S扇形=____.
2、已知扇形面积为 ,圆心角为60°,则这个
扇形的半径R=____.
3、已知半径为2cm的扇形,其弧长为 ,
则这个扇形的面积是_________.
随堂训练
4、(07·内江)如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为120°,OC
长为8cm,CA长为12
cm,则贴纸部分的面
积为( )
A. B.
C. D.
5.课本P114【习题24.4】第1题(1)、(2)
例1.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。
0
B
A
C
D
S弓形= S扇形- S△
例题点评
练习:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。
0
A
B
D
C
E
变式训练
S弓形= S扇形+S△
感悟:
①当弓形面积小于半圆时
S弓形= S扇形-S△
②当弓形面积大于半圆时
S弓形= S扇形+S△
效果检测
3. 已知等边三角形ABC的边长为a,分别以A、B、C为圆心,以 为半径的圆相切于点D、 E、F,求图中阴影部分的面积S.
A.
B.
C.
D.
1.(08·眉山)如图,等边△ABC
的边长为12cm,
切
边BC于D点,
则图中阴影部分的
内切⊙O
面积为( )
C
当堂训练
当堂训练
O
2.(08·潍坊)如图,正六边形内接于圆O,
圆O
的半径为10,则圆中阴影部分的面积为______.
6、(2009年长春)如图,方格纸中4个
小正方形的边长均为1,则图中阴影部分三个
小扇形的面积和为 (结果保留
).
随堂训练
2. (2006,武汉)如图,⊙A、⊙B、⊙C、⊙D相互外离,它们的半径都是1,顺次连接四个圆心得到四边形ABCD,则图形中四个扇形(空白部分)的面积之和是___________.
点击中考
3.(2007,山东)如图所示,分别以n边形的顶点为圆心,以单位1为半径画圆,则图中阴影部分的面积之和为 个平方单位.
点击中考
6. (08·鄂州)如图,Rt△ABC中,∠C=90°, ∠A=30°,BC=2,O、H分别为AB、AC
的中点,将
△ABC顺时针旋转120°到△A1BC1的位置,则整
个旋转过程中线段OH所扫过的面积为( )
B.
C. D.
A
H
B
O
C
H1
O1
A1
C1
C
当堂训练
小 结 :
2. 扇形面积公式与弧长公式的区别:
S扇形= S圆
360
n
l弧= C圆
360
n
1. 扇形的面积大小与哪些因素有关?
(1)与圆心角的大小有关
(2)与半径的长短有关
3. 扇形面积单位与弧长单位的区别:
(1)扇形面积单位有平方的
(2)弧长单位没有平方的
颗粒归仓
1.弧长公式:
2.扇形面积公式:
注意:
(1)两个公式的联系和区别;
(2)两个公式的逆向应用。
努力是半径R,恒心是圆心角n,学习上的收获好比扇形面积S,只有你努力与恒心不断的变大变长你的学习才能有更大的收获面积。
教师寄语
作业:P56
