湘教版九年级下册第二章 2.5 直线与圆的位置关系 课件(共17张PPT)
文档属性
| 名称 | 湘教版九年级下册第二章 2.5 直线与圆的位置关系 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 219.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 11:13:13 | ||
图片预览




文档简介
(共17张PPT)
如图A是⊙O外的一点,AO的延长线交⊙O于C,直线AB经过⊙O上一点B,且AB=BC,∠C=30°. 求证:直线AB是⊙O的切线.
证明:连结OB,
∵OB=OC,AB=BC,∠C=30°
∴∠OBC=∠C=∠A=30°
∴∠AOB=∠C+∠OBC=60°
∴∠ABO=180°-(∠AOB+∠A)
=180°-(60°+30°)
=90°
∴ AB是⊙O的切线.
判断的依据是什么?
课前检测
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线.
判定直线与圆相切有哪些方法?
复习:
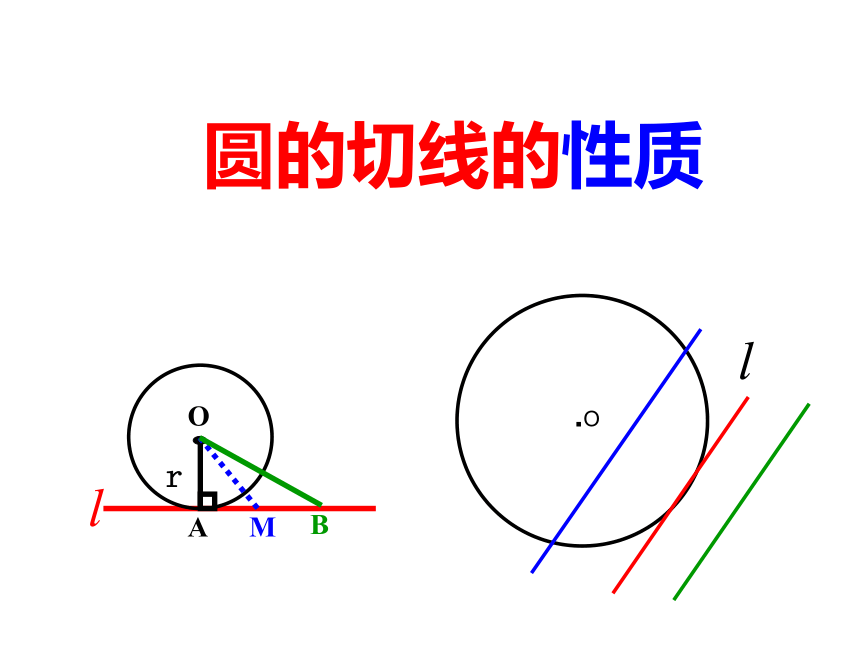
圆的切线的性质
.O
B
A
O
r
M
学习目标:
1、理解切线的性质定理
2、并会利用切线的判定与性质解决问题.
探究
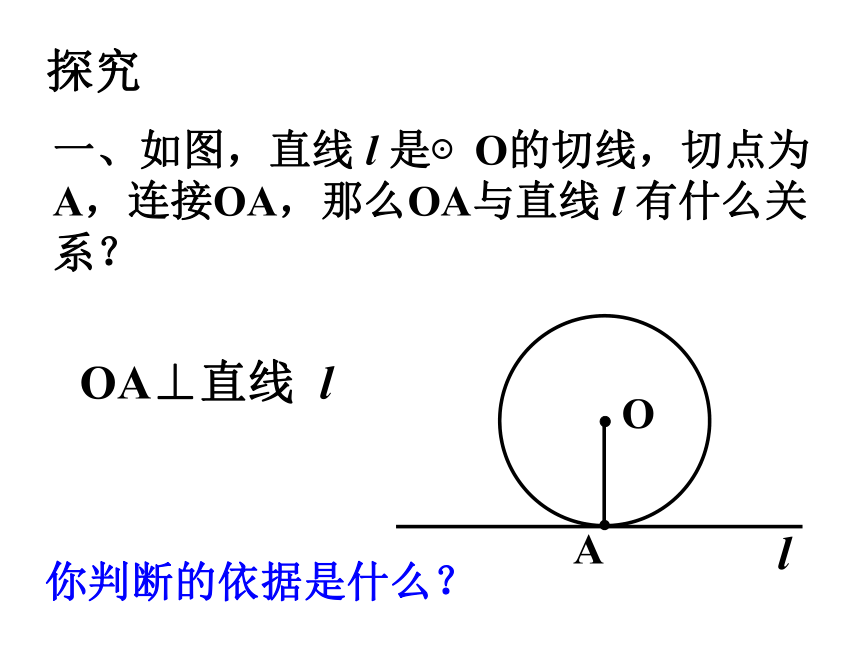
一、如图,直线 l 是⊙O的切线,切点为A,连接OA,那么OA与直线 l 有什么关系?
O
A
l
OA⊥直线 l
你判断的依据是什么?
如果直线L是圆O的切线,切点为A,那么半径OA与直线L是不是垂直呢?
A
O
L
分析:假设OA与L不垂直,
A
O
L
M
过点作OM⊥L,垂足为M。
根据垂线段最短的性质,
有OM﹤OA,
这说明圆心O到直线L的
距离小于半径OA,
于是直线L就要与圆相交,
而这与直线L是圆O的切线相矛盾。
因此,OA与直线L垂直。
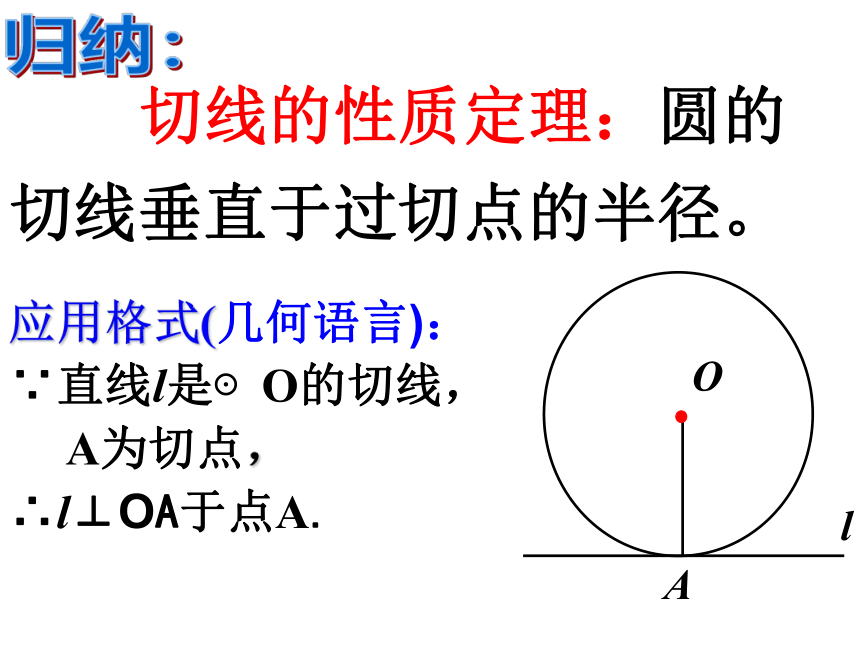
切线的性质定理:圆的切线垂直于过切点的半径。
归纳:
O
A
l
应用格式(几何语言):
∵直线l是⊙O的切线,
A为切点,
∴l⊥OA于点A.
思考:如图,已知AB为⊙O 切线,
切点如何确定?
o
B
A
推论1:经过圆心垂直于切线的直线必过切点
C
思考:如图,已知AB为⊙O 切线,切点为
C,圆心在哪儿?
B
A
推论2:经过切点垂直于切线的直线必过圆心
C
o
1.按图填空:(口答)
(1). 如果AB切⊙O于A,
那么
A
O
B
⊙O的切线
(2). 如果半径OA⊥AB,那么AB是
切点
(3).如果AB是⊙O的切线,OA⊥AB,
那么A是
⊥
OA
AB.
2.下列结论,对的是( )
A. 圆的切线必垂直于半径
B. 垂直于切线的直线必经过圆心
C.垂直于切线的直线必经过切点
D.经过圆心与切点的直线必垂直于切线
D
例1 、如图,AB是⊙O的弦,PA是⊙O的切线,A是切点, ∠PAB=30°,求∠AOB、 ∠P的度数
P
A
B
o
例2 如图,AB是⊙O的直径, C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D. 求证:AC平分∠DAB.
A
O
D
C
B
证明:连接OC.
∵CD 是⊙O的切线,
∴OC⊥CD.
又∵AD⊥CD , ∴OC//AD.
∴∠ACO= ∠CAD .
又∵OC=OD,
∴∠CAO= ∠ACO
∴∠CAD= ∠CAO ,
故AC平分∠DAB.
1、见导学案。
2 、能力提升
如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.
求:(1)∠ADC的度数;(2)AC的长.
当堂检测:
通过这节课的学习:
我学会了……
我还感到疑惑的是……
学习目标:
1、理解切线的性质定理
2、并会利用切线的判定
与性质解决问题.
小结
切线的性质定理:
圆的切线垂直于经过切点的半径。
切线的用法:
见切点,连结圆心和切点得半径,得垂直。
作业:
1.“探究在线”46页7 --13题
2.“探究在线”46页14题
如图A是⊙O外的一点,AO的延长线交⊙O于C,直线AB经过⊙O上一点B,且AB=BC,∠C=30°. 求证:直线AB是⊙O的切线.
证明:连结OB,
∵OB=OC,AB=BC,∠C=30°
∴∠OBC=∠C=∠A=30°
∴∠AOB=∠C+∠OBC=60°
∴∠ABO=180°-(∠AOB+∠A)
=180°-(60°+30°)
=90°
∴ AB是⊙O的切线.
判断的依据是什么?
课前检测
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线.
判定直线与圆相切有哪些方法?
复习:
圆的切线的性质
.O
B
A
O
r
M
学习目标:
1、理解切线的性质定理
2、并会利用切线的判定与性质解决问题.
探究
一、如图,直线 l 是⊙O的切线,切点为A,连接OA,那么OA与直线 l 有什么关系?
O
A
l
OA⊥直线 l
你判断的依据是什么?
如果直线L是圆O的切线,切点为A,那么半径OA与直线L是不是垂直呢?
A
O
L
分析:假设OA与L不垂直,
A
O
L
M
过点作OM⊥L,垂足为M。
根据垂线段最短的性质,
有OM﹤OA,
这说明圆心O到直线L的
距离小于半径OA,
于是直线L就要与圆相交,
而这与直线L是圆O的切线相矛盾。
因此,OA与直线L垂直。
切线的性质定理:圆的切线垂直于过切点的半径。
归纳:
O
A
l
应用格式(几何语言):
∵直线l是⊙O的切线,
A为切点,
∴l⊥OA于点A.
思考:如图,已知AB为⊙O 切线,
切点如何确定?
o
B
A
推论1:经过圆心垂直于切线的直线必过切点
C
思考:如图,已知AB为⊙O 切线,切点为
C,圆心在哪儿?
B
A
推论2:经过切点垂直于切线的直线必过圆心
C
o
1.按图填空:(口答)
(1). 如果AB切⊙O于A,
那么
A
O
B
⊙O的切线
(2). 如果半径OA⊥AB,那么AB是
切点
(3).如果AB是⊙O的切线,OA⊥AB,
那么A是
⊥
OA
AB.
2.下列结论,对的是( )
A. 圆的切线必垂直于半径
B. 垂直于切线的直线必经过圆心
C.垂直于切线的直线必经过切点
D.经过圆心与切点的直线必垂直于切线
D
例1 、如图,AB是⊙O的弦,PA是⊙O的切线,A是切点, ∠PAB=30°,求∠AOB、 ∠P的度数
P
A
B
o
例2 如图,AB是⊙O的直径, C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D. 求证:AC平分∠DAB.
A
O
D
C
B
证明:连接OC.
∵CD 是⊙O的切线,
∴OC⊥CD.
又∵AD⊥CD , ∴OC//AD.
∴∠ACO= ∠CAD .
又∵OC=OD,
∴∠CAO= ∠ACO
∴∠CAD= ∠CAO ,
故AC平分∠DAB.
1、见导学案。
2 、能力提升
如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.
求:(1)∠ADC的度数;(2)AC的长.
当堂检测:
通过这节课的学习:
我学会了……
我还感到疑惑的是……
学习目标:
1、理解切线的性质定理
2、并会利用切线的判定
与性质解决问题.
小结
切线的性质定理:
圆的切线垂直于经过切点的半径。
切线的用法:
见切点,连结圆心和切点得半径,得垂直。
作业:
1.“探究在线”46页7 --13题
2.“探究在线”46页14题
