北师大版七年级数学下册2.1 两条直线的位置关系第一课时课件(共25张PPT)
文档属性
| 名称 | 北师大版七年级数学下册2.1 两条直线的位置关系第一课时课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 10:54:22 | ||
图片预览







文档简介
(共25张PPT)
学习目标
1.了解平面内两条直线的位置关系;
2.理解对顶角、补角、余角等概念,
并掌握其性质;
3.在应用中,发展、推理能
力和初步的几何语言表达能力.
西安钟楼
建于明太祖洪武十七年年是中国现存钟楼中形制最大、保存最完整的一座.
水脉、绿脉、文脉有机融合,形成了以融合三国文化、都市生态文化和魏都风情文化为一体的曹魏故都水利风景区.
港阔水深,为天然良港,香港亦因其而拥有“东方之珠”、“世界三大夜景”之美誉。维多利亚港一直影响香港的历史和文化.
两条直线的位置关系
第一课时
在同一平面内,
两条直线的位置关系
相交
平行
1.若两条直线只有一个公共点,我们称这两条直线为相交线.
2.在同一平面内,不相交的两条直线
叫做平行线.
归纳概念
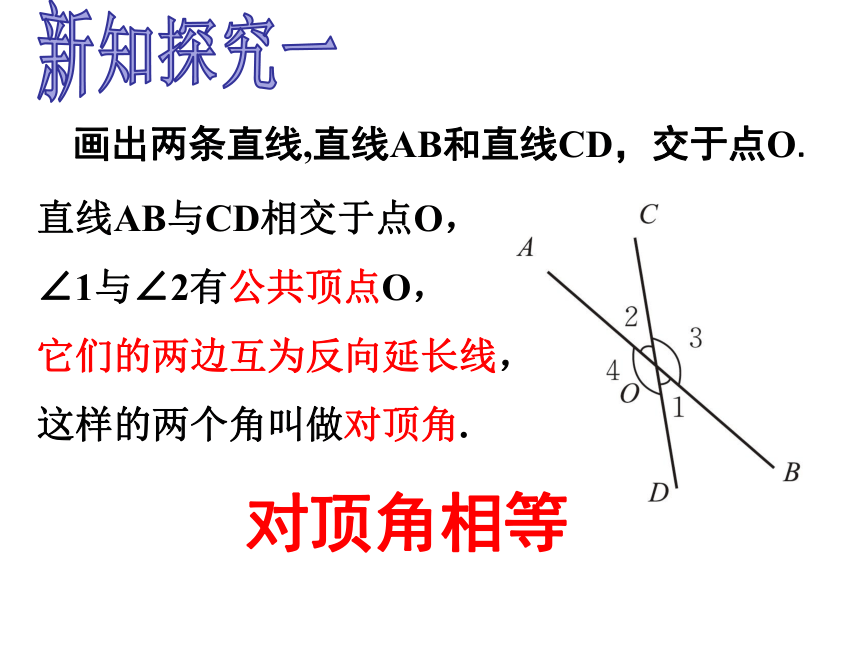
画出两条直线,直线AB和直线CD,交于点O.
直线AB与CD相交于点O,
∠1与∠2有公共顶点O,
它们的两边互为反向延长线,
这样的两个角叫做对顶角.
对顶角相等
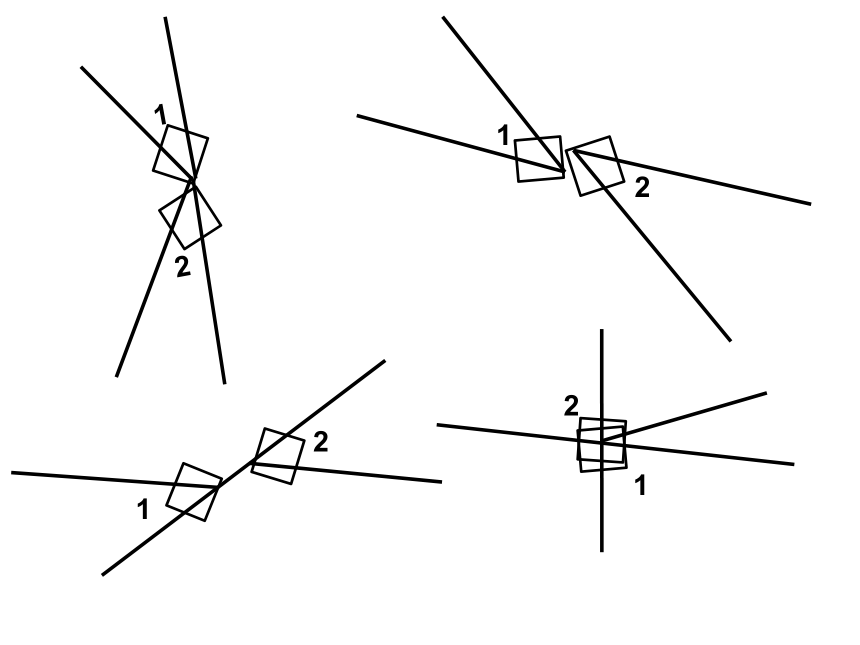
1
2
1
2
1
2
1
2
实际应用:有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
1
2
3
在图中,∠1和∠3有什么
数量关系?
图中还有哪些角是互为补角?
如果两个角的和是180°,那么称这两个角互为补角.
如果两个角的和是90°,那么称这两个角互为余角.
互余与互补是指两个角之间的数量关系,与它们的位置无关.
跃跃欲试
不如一试
巩固练习:下列说法正确的有 。
①已知∠A=40°,则∠A的余角等于50°.
②若∠1+∠2=180°,则∠1和∠2互为补角.
③若∠1+∠2+∠3=180°,则∠1、∠2、∠3互补.
④一个角的补角必为钝角.
⑤两个角互余与其位置有关系.
∠1=∠2
小组合作交流,解决下列问题:
问题:图中有哪些角互余?
将实物图抽象简化成几何图形,ON与DC交于点O,∠DON=∠CON=90°,∠1=∠2
同角或等角的余角相等
小组合作交流,解决下列问题:
问题:图中有哪些角互补?
将实物图抽象简化成几何图形,ON与DC交于点O,∠DON=∠CON=90°,∠1=∠2
同角或等角的补角相等
同角的补角相等
问题:为什么对顶角相等?
通过本节课的探索与交流——
你学到了哪些知识····
你还有哪些困惑····
归纳小结反思提高
1.用你手中的三角板,画一个直角三角形,如图.则∠A是∠B的 。
在上题的基础上,作∠CDA=90°.
(1)右图中有哪些角互余?
(2)哪些角互补?
(3)你还能提出哪些问题?试试看吧!
C
A
B
比比看,谁提的问题更独特!加油~
C
A
B
D
2.如图,将一个长方形纸片沿着直线EF折叠,点C落在点H处;再将∠D沿着GE折叠,使DE落在直线EH上:
问题1:∠FEG等于多少度?为什么?
问题2:上述折纸的图形中,还有哪些角互为余角?哪些角互为补角?
A
B
G
D
E
F
C
D'
H
1.校本作业第二章第一课时基础巩固,能力提升部分.
2.延伸拓展选作.
3.预习第二课时并完成预习准备.
感谢您的到来
期待您的指导
学习目标
1.了解平面内两条直线的位置关系;
2.理解对顶角、补角、余角等概念,
并掌握其性质;
3.在应用中,发展、推理能
力和初步的几何语言表达能力.
西安钟楼
建于明太祖洪武十七年年是中国现存钟楼中形制最大、保存最完整的一座.
水脉、绿脉、文脉有机融合,形成了以融合三国文化、都市生态文化和魏都风情文化为一体的曹魏故都水利风景区.
港阔水深,为天然良港,香港亦因其而拥有“东方之珠”、“世界三大夜景”之美誉。维多利亚港一直影响香港的历史和文化.
两条直线的位置关系
第一课时
在同一平面内,
两条直线的位置关系
相交
平行
1.若两条直线只有一个公共点,我们称这两条直线为相交线.
2.在同一平面内,不相交的两条直线
叫做平行线.
归纳概念
画出两条直线,直线AB和直线CD,交于点O.
直线AB与CD相交于点O,
∠1与∠2有公共顶点O,
它们的两边互为反向延长线,
这样的两个角叫做对顶角.
对顶角相等
1
2
1
2
1
2
1
2
实际应用:有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
1
2
3
在图中,∠1和∠3有什么
数量关系?
图中还有哪些角是互为补角?
如果两个角的和是180°,那么称这两个角互为补角.
如果两个角的和是90°,那么称这两个角互为余角.
互余与互补是指两个角之间的数量关系,与它们的位置无关.
跃跃欲试
不如一试
巩固练习:下列说法正确的有 。
①已知∠A=40°,则∠A的余角等于50°.
②若∠1+∠2=180°,则∠1和∠2互为补角.
③若∠1+∠2+∠3=180°,则∠1、∠2、∠3互补.
④一个角的补角必为钝角.
⑤两个角互余与其位置有关系.
∠1=∠2
小组合作交流,解决下列问题:
问题:图中有哪些角互余?
将实物图抽象简化成几何图形,ON与DC交于点O,∠DON=∠CON=90°,∠1=∠2
同角或等角的余角相等
小组合作交流,解决下列问题:
问题:图中有哪些角互补?
将实物图抽象简化成几何图形,ON与DC交于点O,∠DON=∠CON=90°,∠1=∠2
同角或等角的补角相等
同角的补角相等
问题:为什么对顶角相等?
通过本节课的探索与交流——
你学到了哪些知识····
你还有哪些困惑····
归纳小结反思提高
1.用你手中的三角板,画一个直角三角形,如图.则∠A是∠B的 。
在上题的基础上,作∠CDA=90°.
(1)右图中有哪些角互余?
(2)哪些角互补?
(3)你还能提出哪些问题?试试看吧!
C
A
B
比比看,谁提的问题更独特!加油~
C
A
B
D
2.如图,将一个长方形纸片沿着直线EF折叠,点C落在点H处;再将∠D沿着GE折叠,使DE落在直线EH上:
问题1:∠FEG等于多少度?为什么?
问题2:上述折纸的图形中,还有哪些角互为余角?哪些角互为补角?
A
B
G
D
E
F
C
D'
H
1.校本作业第二章第一课时基础巩固,能力提升部分.
2.延伸拓展选作.
3.预习第二课时并完成预习准备.
感谢您的到来
期待您的指导
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
