2021-2022学年苏科版七年级数学下册9.5多项式的因式分解(1)课件(16张)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册9.5多项式的因式分解(1)课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 102.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 11:19:22 | ||
图片预览






文档简介
(共16张PPT)
9.5 多项式的因式分解(1)
七年级(下册)
初中数学
活动一:如何计算1.25×16了?并说出你为什么要这样做了?
合数可以分解几个质因数如16=2×8,16=2×2×2×2×2,那么你能举出同样的例子吗?
活动二:一个多项式能否进行分解几个整式相乘了?我们知道a(b+c+d)=ab+ac+ad,那么ab+ac+ad= a(b+c+d)可以吗?你能够举出几个这样的例子吗?
填空, 并说说你的方法:
(1) a2b+ab2 = ab( )
(2) 3x2-6x3 = 3x2( )
(3) 9abc-6a2b2+12abc2 = 3ab( )
像这样,把一个多项式写成几个整式的积的形式叫做多项式的因式分解.
想一想 :因式分解的依据是什么
自主探索
a+b
1-2 x
3c-2ab+4c2
活动三:你能否说出因式分解与整式乘法之间有什么关系了?
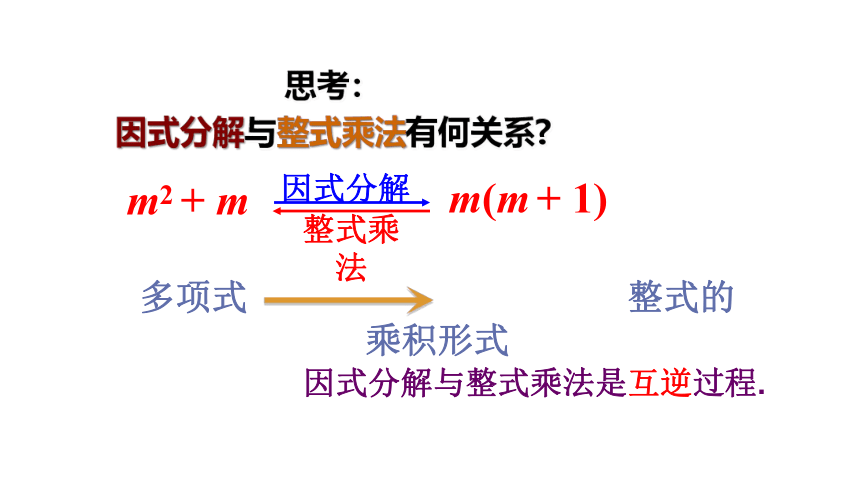
思考:
因式分解与整式乘法有何关系
整式乘法
m2 + m
因式分解
因式分解与整式乘法是互逆过程.
多项式 整式的乘积形式
m(m + 1)
你能把多项式 ab+ac+ad 写成积的形式吗
请说明你的理由.
ab+ac+ad =a(b+c+d )
自主探索
观察多项式 ab+ac+ad 的每一项,你有什么发现?
a 是多项式 ab+ac+ad 各项都含有的因式.
一个多项式各项都含有的因式,称为这个多项式各项的公因式.
找出下列多项式各项的公因式,并填写下表.
多项式 公因式
4x+4y
a2b2+ab2
3x2-6x3
9abc-6a2b2+12abc2
结合填表过程,你能归纳出找一个多项式的公因式的方法吗?
试一试
ab2
4
3x2
3ab
分三个步骤:
一看系数:
取各项系数的最大公约数;
二看字母:
取多项式中各项都含有的相同字母.
三看指数:
相同字母的指数取次数最低的.
多项式各项都含有的因式
一看系数:取各项系数的最大公约数.
二看字母:取多项式中各项都含有的相同字母.
三看指数:相同字母的指数取次数最低的.
写出下列多项式各项的公因式:
(1) ab + 2a2b - 3ab2 .
(2) 6mn2 - 18m2n2 + 24m3n3 .
(3) 7x2y - 14xy2z - 35xyz2 .
练一练
下列各式由左到右的变形哪些是因式分解 哪些不是 并思考因式分解与整式的乘法有何关系
(1) ab+ac+d = a(b+c) +d
(2) a2-1 = (a+1)(a-1)
(3) (a+1)(a-1)=a2-1
(4) 8a2b3c = 2a2·2b3·2c
练一练
把一个多项式写成几个整式的积的形式叫做多项式的因式分解.
= 5x2 ( )
例1 把 5x3-10x2 分解因式:
例题讲解
把多项式分解成公因式与另一个因式的积的形式,这种分解因式的方法,叫做提公因式法.
练一练:
把下列各式分解因式:
(1) 12ab2c-6ab;
(2) 4x2-12x3.
解:
原式=
5x2
· x
- 5x2
· 2
x-2
步骤:
一找;
二分;
三提.
- 2m3+8m2-12m
例2 分解因式:
当多项式的第一项的系数为负数时,通常把“-”作为公因式的符号,再因式分解,从而使分解后括号内第一项的系数为 “+”.
例题讲解
练一练:把 下列各式分解因式:
(1) - 3ab3 + 15a2b2 ; (2) - x2y + 4xy - 5y.
= - 2m ( )
解:
原式=
=- ( )
·m2
-2m
·4m
m2 - 4m + 6
+2m
· 6
- ( )
2m3-8m2+12m
2m
如何把多项式 3a(x+y)-2b(x+y)分解因式
多项式的公因式一般来说是一个单项式,但有时也会是一个多项式; 这时只要把那个多项式看成一个整体作为原多项式的公因式即可.
想一想
(x+y)( )
解:
原式=
3a - 2b
变式:如何把多项式 3a(x-y)-2b(y-x)分解因式
=(x - y)( )
解:
原式=
3a +2b
3a(x-y)
+2b(x-y)
把下列各式分解因式:
(1)x(a+b)-y(a+b);
(2)a(x-a)+b(a-x)-c(x-a).
练一练
区别:
联系:
因式分解与整式乘法有什么联系和区别?
思考
整式乘法:有几个整式的积的形式转化成一个多项式的形式.
因式分解:有一个多项式的形式转化成几个整式的积的形式.
多项式的因式分解与整式乘法是两种相反方向的变形,它们互为逆过程.
(1) 20042+2004能被2005整除吗
(2) 如果n是自然数,那么n2+n是奇数还是偶数
课后思考
9.5 多项式的因式分解(1)
七年级(下册)
初中数学
活动一:如何计算1.25×16了?并说出你为什么要这样做了?
合数可以分解几个质因数如16=2×8,16=2×2×2×2×2,那么你能举出同样的例子吗?
活动二:一个多项式能否进行分解几个整式相乘了?我们知道a(b+c+d)=ab+ac+ad,那么ab+ac+ad= a(b+c+d)可以吗?你能够举出几个这样的例子吗?
填空, 并说说你的方法:
(1) a2b+ab2 = ab( )
(2) 3x2-6x3 = 3x2( )
(3) 9abc-6a2b2+12abc2 = 3ab( )
像这样,把一个多项式写成几个整式的积的形式叫做多项式的因式分解.
想一想 :因式分解的依据是什么
自主探索
a+b
1-2 x
3c-2ab+4c2
活动三:你能否说出因式分解与整式乘法之间有什么关系了?
思考:
因式分解与整式乘法有何关系
整式乘法
m2 + m
因式分解
因式分解与整式乘法是互逆过程.
多项式 整式的乘积形式
m(m + 1)
你能把多项式 ab+ac+ad 写成积的形式吗
请说明你的理由.
ab+ac+ad =a(b+c+d )
自主探索
观察多项式 ab+ac+ad 的每一项,你有什么发现?
a 是多项式 ab+ac+ad 各项都含有的因式.
一个多项式各项都含有的因式,称为这个多项式各项的公因式.
找出下列多项式各项的公因式,并填写下表.
多项式 公因式
4x+4y
a2b2+ab2
3x2-6x3
9abc-6a2b2+12abc2
结合填表过程,你能归纳出找一个多项式的公因式的方法吗?
试一试
ab2
4
3x2
3ab
分三个步骤:
一看系数:
取各项系数的最大公约数;
二看字母:
取多项式中各项都含有的相同字母.
三看指数:
相同字母的指数取次数最低的.
多项式各项都含有的因式
一看系数:取各项系数的最大公约数.
二看字母:取多项式中各项都含有的相同字母.
三看指数:相同字母的指数取次数最低的.
写出下列多项式各项的公因式:
(1) ab + 2a2b - 3ab2 .
(2) 6mn2 - 18m2n2 + 24m3n3 .
(3) 7x2y - 14xy2z - 35xyz2 .
练一练
下列各式由左到右的变形哪些是因式分解 哪些不是 并思考因式分解与整式的乘法有何关系
(1) ab+ac+d = a(b+c) +d
(2) a2-1 = (a+1)(a-1)
(3) (a+1)(a-1)=a2-1
(4) 8a2b3c = 2a2·2b3·2c
练一练
把一个多项式写成几个整式的积的形式叫做多项式的因式分解.
= 5x2 ( )
例1 把 5x3-10x2 分解因式:
例题讲解
把多项式分解成公因式与另一个因式的积的形式,这种分解因式的方法,叫做提公因式法.
练一练:
把下列各式分解因式:
(1) 12ab2c-6ab;
(2) 4x2-12x3.
解:
原式=
5x2
· x
- 5x2
· 2
x-2
步骤:
一找;
二分;
三提.
- 2m3+8m2-12m
例2 分解因式:
当多项式的第一项的系数为负数时,通常把“-”作为公因式的符号,再因式分解,从而使分解后括号内第一项的系数为 “+”.
例题讲解
练一练:把 下列各式分解因式:
(1) - 3ab3 + 15a2b2 ; (2) - x2y + 4xy - 5y.
= - 2m ( )
解:
原式=
=- ( )
·m2
-2m
·4m
m2 - 4m + 6
+2m
· 6
- ( )
2m3-8m2+12m
2m
如何把多项式 3a(x+y)-2b(x+y)分解因式
多项式的公因式一般来说是一个单项式,但有时也会是一个多项式; 这时只要把那个多项式看成一个整体作为原多项式的公因式即可.
想一想
(x+y)( )
解:
原式=
3a - 2b
变式:如何把多项式 3a(x-y)-2b(y-x)分解因式
=(x - y)( )
解:
原式=
3a +2b
3a(x-y)
+2b(x-y)
把下列各式分解因式:
(1)x(a+b)-y(a+b);
(2)a(x-a)+b(a-x)-c(x-a).
练一练
区别:
联系:
因式分解与整式乘法有什么联系和区别?
思考
整式乘法:有几个整式的积的形式转化成一个多项式的形式.
因式分解:有一个多项式的形式转化成几个整式的积的形式.
多项式的因式分解与整式乘法是两种相反方向的变形,它们互为逆过程.
(1) 20042+2004能被2005整除吗
(2) 如果n是自然数,那么n2+n是奇数还是偶数
课后思考
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
