28.1特殊角的三角函数
文档属性
| 名称 | 28.1特殊角的三角函数 |  | |
| 格式 | zip | ||
| 文件大小 | 218.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-10 21:54:21 | ||
图片预览



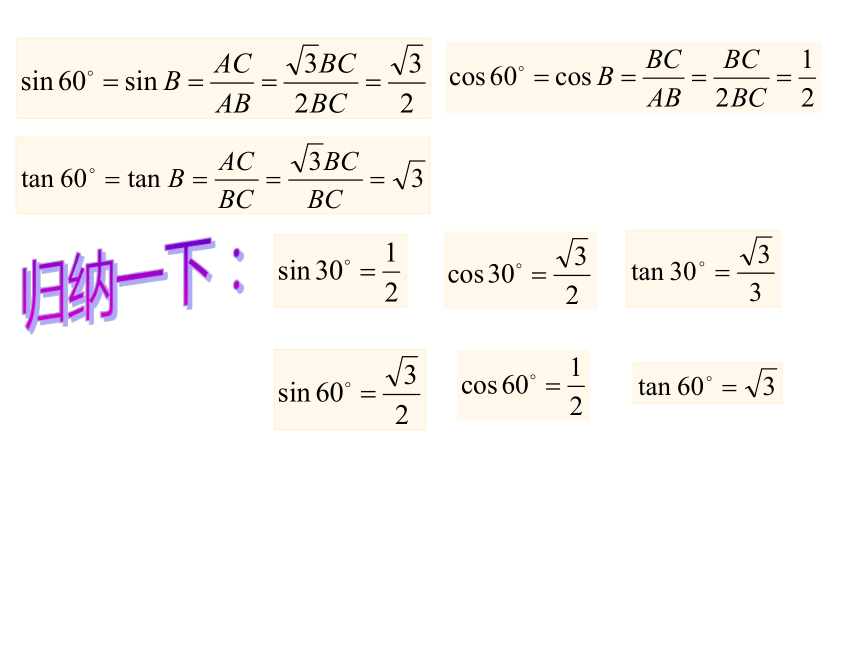



文档简介
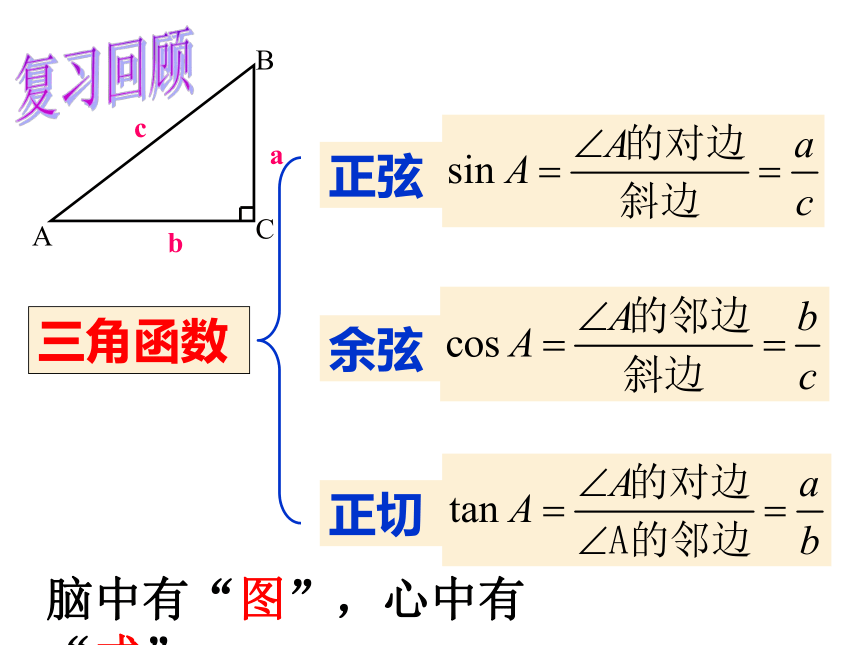
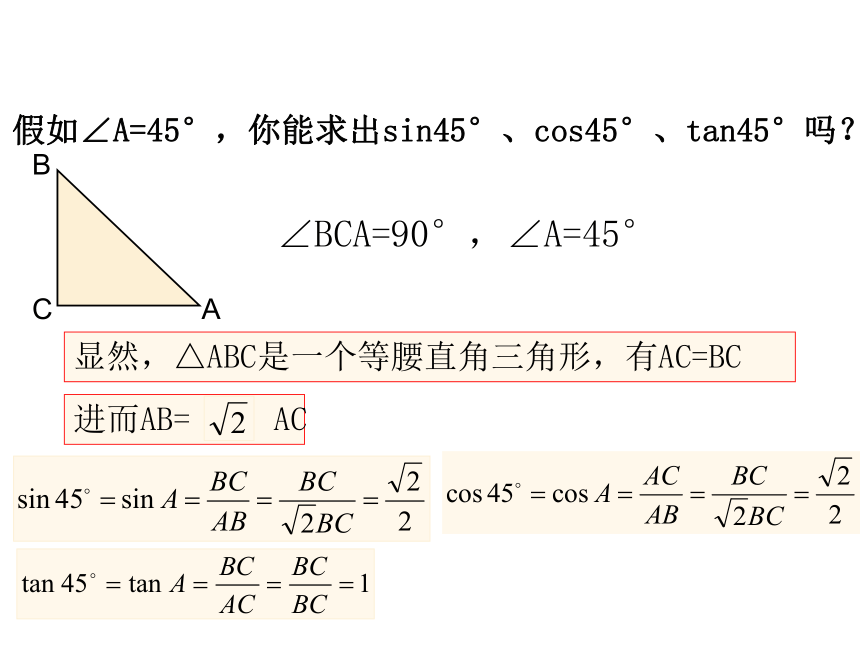
课件25张PPT。特殊角的三角函数值三角函数 正弦 余弦 正切 abc脑中有“图”,心中有“式”复习回顾假如∠A=30°,你能求出sin30°,cos30°,tan30°吗?②用计算器①度量,用定义还有其他方法吗?整体感知CAB∠BCA=90°,∠A=30°D可以知道,∠B=60°,CD=BD=AD=0.5AB进而,△BCD是一等边三角形, AB=2BC还可以求出AC= BC那么,此时, sin60°、cos60°、tan60°你可以求出来吗?归纳一下:假如∠A=45°,你能求出sin45°、cos45°、tan45°吗?CAB显然,△ABC是一个等腰直角三角形,有AC=BC∠BCA=90°,∠A=45°进而AB= AC归纳一下:一定要记住哦!快速抢答:(看谁又快又准!)熟悉之后反过来已知特殊值求角度。快速抢答:(看谁又快又准!)1角α三角函数 认真观察一下特殊角三角函数值表格,你能发现什么规律?重点研读锐角三角函数的增减性一个锐角的正弦值与正切值随着角度的增大而增大;
一个锐角的余弦值随着角度的增大而减小火眼金睛火眼金睛同角之间的三角函数的关系平方和关系:商的关系:火眼金睛1、2sin30°- cos45°2、sin230°+ cos230°针对性练习练习2:求锐角 的度数:请你谈谈对本节学习内容的体会和感受。
课堂小结堂上清3.已知∠A为锐角,且cosA≤ ,那么( )
A. 0°<∠A≤60° B 60°≤∠A<0°
C . 0°<∠A≤30° D 30°≤ ∠A ≤ 90°
4.若(tanA-3)2+│2cosB-│=0,则△ABC( ).
A.是直角三角形 B.是等边三角形
C.是含有60°的任意三角形 D.是顶角为钝角的等腰三角形 5、 如图,在四边形ABCD中, ∠A=60°, ∠B=∠D=90°, BC=2,CD=3, 求四边形ABCD的面积.23E60°(2).链接中招4.已知∠A为锐角,且cosA≤ ,那么( )
A.0°<∠A≤60°B60°≤∠A<0°
C0°<∠A≤30°D30°≤90°
5.若(tanA-3)2+│2cosB-│=0,则△ABC( ).
A.是直角三角形 B.是等边三角形
C.是含有60°的任意三角形 D.是顶角为钝角的等腰三角形 3、如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连结BD,若cos∠BDC= , 求BC的长 3x5x4x5x再见
一个锐角的余弦值随着角度的增大而减小火眼金睛火眼金睛同角之间的三角函数的关系平方和关系:商的关系:火眼金睛1、2sin30°- cos45°2、sin230°+ cos230°针对性练习练习2:求锐角 的度数:请你谈谈对本节学习内容的体会和感受。
课堂小结堂上清3.已知∠A为锐角,且cosA≤ ,那么( )
A. 0°<∠A≤60° B 60°≤∠A<0°
C . 0°<∠A≤30° D 30°≤ ∠A ≤ 90°
4.若(tanA-3)2+│2cosB-│=0,则△ABC( ).
A.是直角三角形 B.是等边三角形
C.是含有60°的任意三角形 D.是顶角为钝角的等腰三角形 5、 如图,在四边形ABCD中, ∠A=60°, ∠B=∠D=90°, BC=2,CD=3, 求四边形ABCD的面积.23E60°(2).链接中招4.已知∠A为锐角,且cosA≤ ,那么( )
A.0°<∠A≤60°B60°≤∠A<0°
C0°<∠A≤30°D30°≤90°
5.若(tanA-3)2+│2cosB-│=0,则△ABC( ).
A.是直角三角形 B.是等边三角形
C.是含有60°的任意三角形 D.是顶角为钝角的等腰三角形 3、如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连结BD,若cos∠BDC= , 求BC的长 3x5x4x5x再见
