北师大版八年级数学下册 1.3 线段的垂直平分线课件 (共14张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 1.3 线段的垂直平分线课件 (共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 25.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 12:05:37 | ||
图片预览


文档简介
(共14张PPT)
O
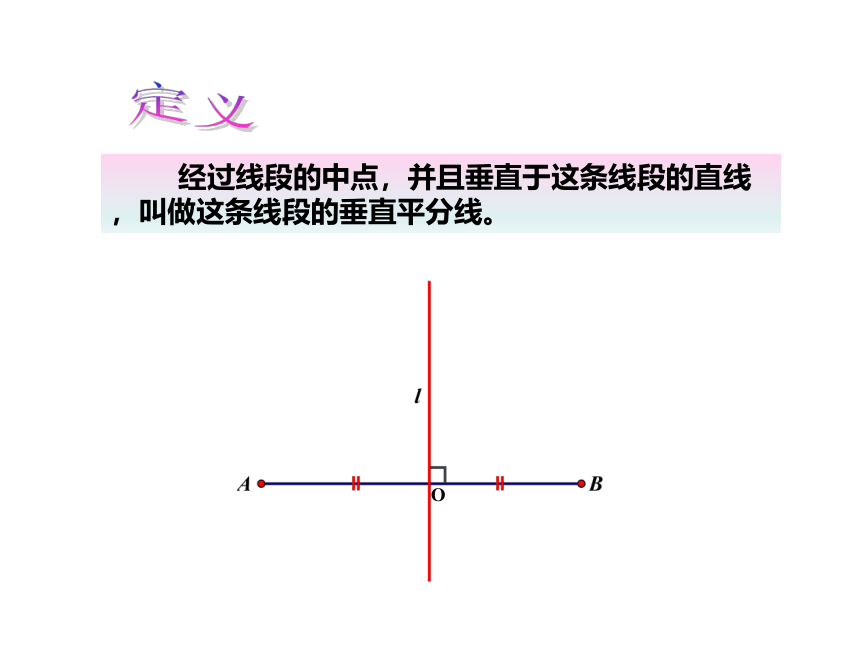
经过线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
1.能够证明线段的垂直平分线的性质定理和判定定理。
2.利用定理解决几何问题。
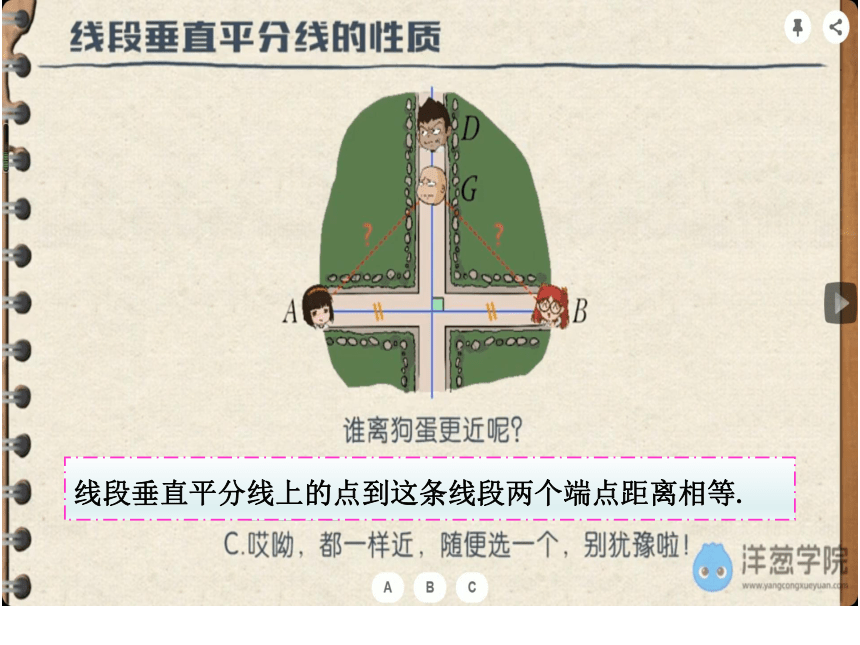
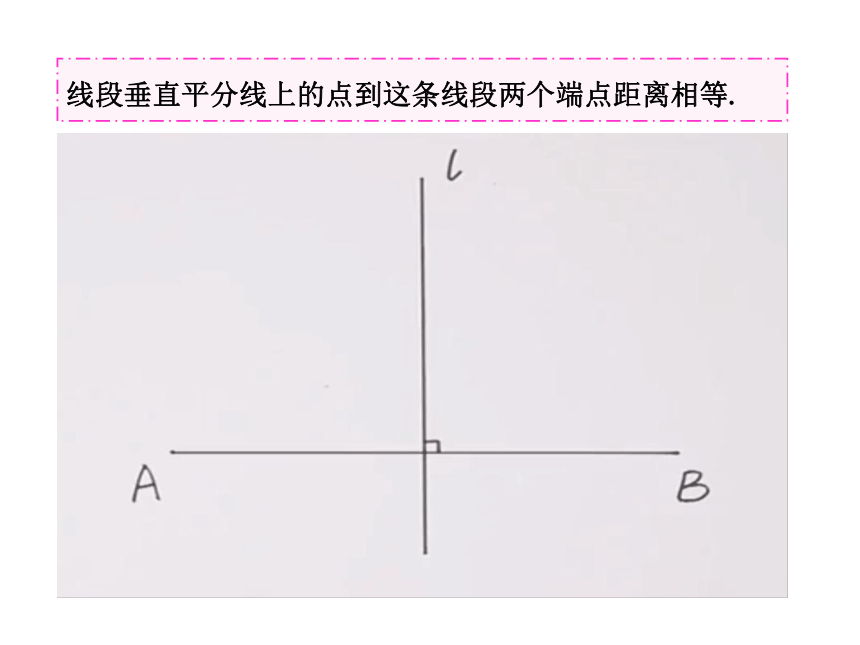
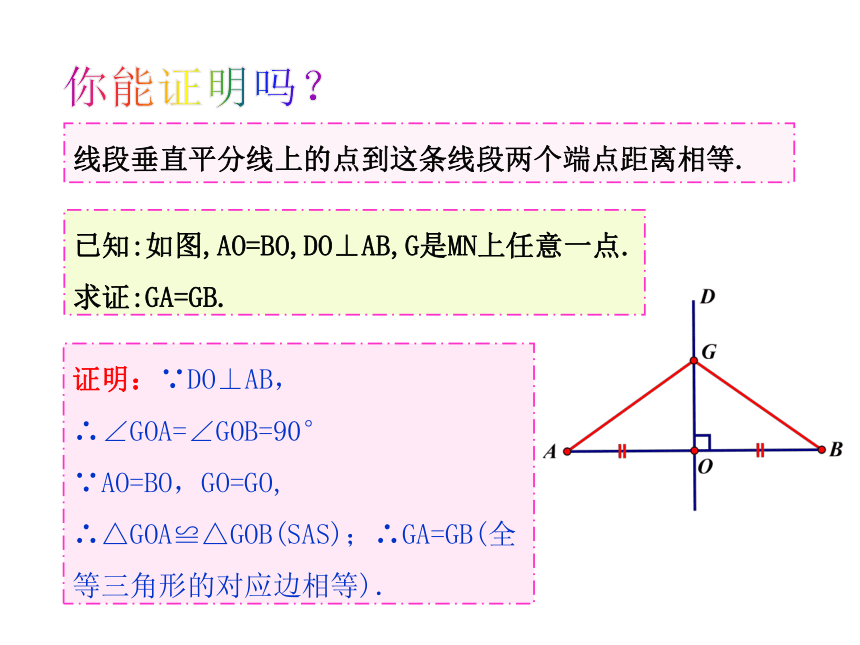
线段垂直平分线上的点到这条线段两个端点距离相等.
线段垂直平分线上的点到这条线段两个端点距离相等.
线段垂直平分线上的点到这条线段两个端点距离相等.
已知:如图,AO=BO,DO⊥AB,G是MN上任意一点. 求证:GA=GB.
证明:∵DO⊥AB,
∴∠GOA=∠GOB=90°
∵AO=BO,GO=GO, ∴△GOA≌△GOB(SAS);∴GA=GB(全等三角形的对应边相等).
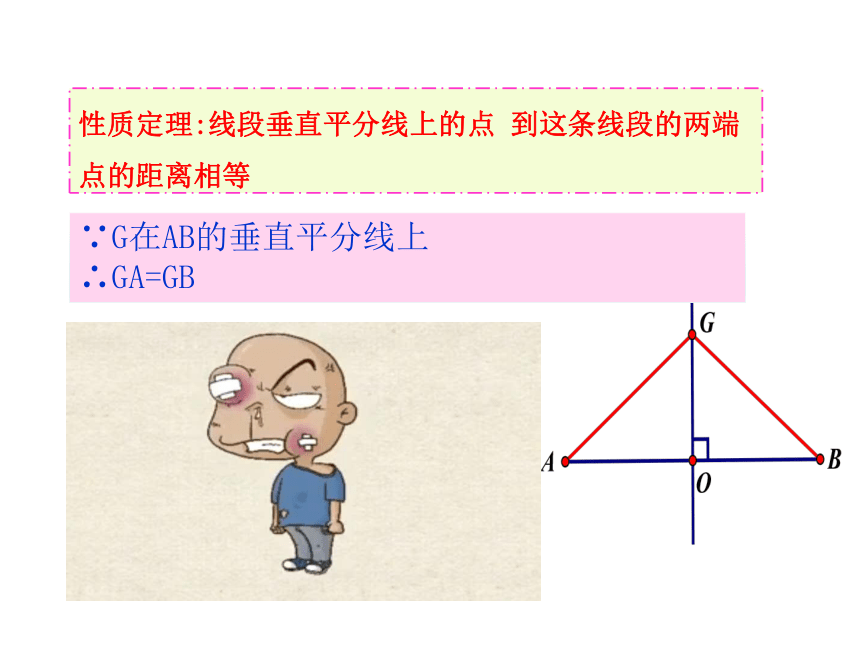
性质定理:线段垂直平分线上的点 到这条线段的两端点的距离相等
∵G在AB的垂直平分线上
∴GA=GB
你能写出这个定理的逆命题吗?
逆命题:到线段两个端点的距离相等的点在这条线段的垂直平分线上。
当我们写出逆命题时,就想到判断它的真假.如果真,则需证明它;如果假,则需用反例说明。
性质定理:线段垂直平分线上的点 到这条线段的两端点的距离相等
B
P
A
C
性质定理的逆命题:到线段两个端点的距离相等的点在这条线段的垂直平分线上.
已知:线段AB,点P是平面内一点且PA=PB。
求证:P点在AB的垂直平分线上。
A
C
B
P
M
N
∵PA=PB(已知),
∴点P在AB的垂直平分线上
温馨提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.
判定定理 :到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
:
1.如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED= cm;如果∠ECD=600,那么∠EDC= 0.
老师期望:
你能说出填空结果的根据.
E
D
A
B
C
7
60
O
经过线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
1.能够证明线段的垂直平分线的性质定理和判定定理。
2.利用定理解决几何问题。
线段垂直平分线上的点到这条线段两个端点距离相等.
线段垂直平分线上的点到这条线段两个端点距离相等.
线段垂直平分线上的点到这条线段两个端点距离相等.
已知:如图,AO=BO,DO⊥AB,G是MN上任意一点. 求证:GA=GB.
证明:∵DO⊥AB,
∴∠GOA=∠GOB=90°
∵AO=BO,GO=GO, ∴△GOA≌△GOB(SAS);∴GA=GB(全等三角形的对应边相等).
性质定理:线段垂直平分线上的点 到这条线段的两端点的距离相等
∵G在AB的垂直平分线上
∴GA=GB
你能写出这个定理的逆命题吗?
逆命题:到线段两个端点的距离相等的点在这条线段的垂直平分线上。
当我们写出逆命题时,就想到判断它的真假.如果真,则需证明它;如果假,则需用反例说明。
性质定理:线段垂直平分线上的点 到这条线段的两端点的距离相等
B
P
A
C
性质定理的逆命题:到线段两个端点的距离相等的点在这条线段的垂直平分线上.
已知:线段AB,点P是平面内一点且PA=PB。
求证:P点在AB的垂直平分线上。
A
C
B
P
M
N
∵PA=PB(已知),
∴点P在AB的垂直平分线上
温馨提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.
判定定理 :到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
:
1.如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED= cm;如果∠ECD=600,那么∠EDC= 0.
老师期望:
你能说出填空结果的根据.
E
D
A
B
C
7
60
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
