人教版七年级数学下册第七章平面直角坐标系中面积问题教学设计
文档属性
| 名称 | 人教版七年级数学下册第七章平面直角坐标系中面积问题教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 97.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 13:43:49 | ||
图片预览

文档简介
第七章平面直角坐标系中面积问题
一、内容和内容解析
1、内容
会用割补法求平面直角坐标系中图形的面积
2、内容解析
“平面直角坐标系”是“数轴”的发展,使点与坐标的对应关系顺利实现了从一维到二维的过渡。“平面直角坐标系”的建立使得有序数对与平面内的点产生了一一对应,提供了用代数方法来解决几何问题的重要数学工具。
本章前几节课中,学生已经能够根据点的坐标表示出它到坐标轴的距离,并且能用平移的知识求出平行或垂直于坐标轴的线段长度。本节课先从平移体会求点坐标的方法,在此基础上又从已知图形面积求顶点坐标的方法,而后设定动点情景来求点的坐标,让学生体会用代数方法解决几何问题的过程。
在平面直角坐标系中不规则的图形,我们只能根据分割图形或者补充图形,使得它变成一个规则的图形来求解面积,构成几何图形的要素是点线面,这与平面直角坐标系中由点的坐标表示线段的长度进而求出图形的面积的研究方法是一致的,体现了数形结合的思想。
由以上分析,可以确定本节课的教学重点:用割补法求图形的面积。
二、目标和目标解析
1、目标
(1)会用割补法求平面直角坐标系中三角形和四边形的面积;
(2)体会从点坐标求线段长进而求出图形面积的过程;
2、目标解析
达成目标(1)的标志是:学生能把平面直角坐标系中倾斜三角形或者四边形通过作辅助线的方法分割或补充成水平或竖直的规则图形来求面积,一般情况下是补充成长方形或梯形。
达成目标(2)的标志是:学生在理解习题思路的基础上,能把已知条件中给出的点坐标转化成线段的长度,进而能够根据面积的大小求出点的坐标。
三、教学重难点
教学重难点是:理解用平行线来找与已知三角形同底等高的三角形,体会满足条件的点的位置的几种可能。
四、教学过程设计
1、复习引入
问题1 回顾已学内容,回答下列问题:
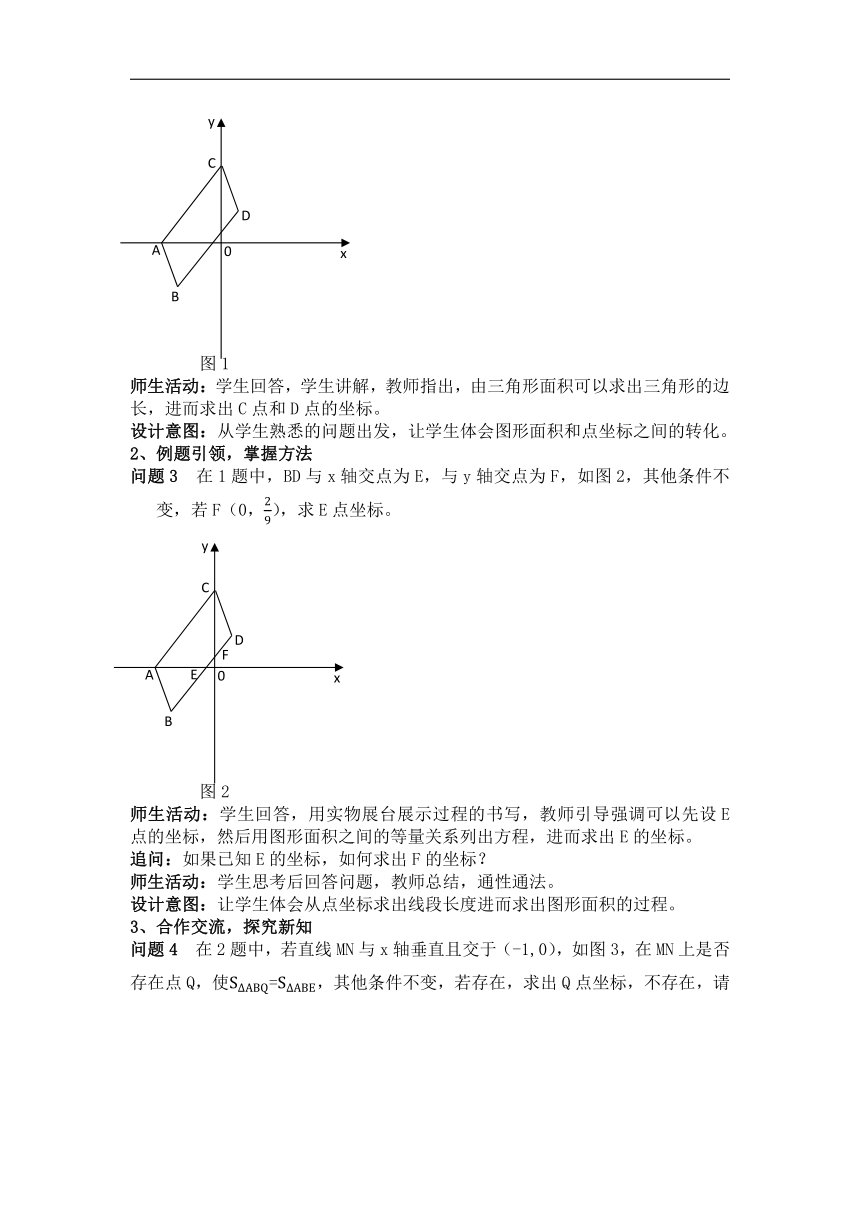
在平面直角坐标系中,如图1,将线段AB平移至线段CD,连接AC,BD。
(1)直接写出图中相等的线段和平行的线段 ;
(2)已知A(-3,0),B(-2,-2),C(0,)则D点坐标为; ;
师生活动:学生回答问题后,教师用几何画板展示动态图形,用平移的知识求出D点的坐标。
问题2 (3)在(2)中,若把“C(0,)”改为=5,其他条件不变,求C,D坐标。
图1
师生活动:学生回答,学生讲解,教师指出,由三角形面积可以求出三角形的边长,进而求出C点和D点的坐标。
设计意图:从学生熟悉的问题出发,让学生体会图形面积和点坐标之间的转化。
2、例题引领,掌握方法
问题3 在1题中,BD与x轴交点为E,与y轴交点为F,如图2,其他条件不变,若F(0,),求E点坐标。
图2
师生活动:学生回答,用实物展台展示过程的书写,教师引导强调可以先设E点的坐标,然后用图形面积之间的等量关系列出方程,进而求出E的坐标。
追问:如果已知E的坐标,如何求出F的坐标?
师生活动:学生思考后回答问题,教师总结,通性通法。
设计意图:让学生体会从点坐标求出线段长度进而求出图形面积的过程。
3、合作交流,探究新知
问题4 在2题中,若直线MN与x轴垂直且交于(-1,0),如图3,在MN上是否存在点Q,使=,其他条件不变,若存在,求出Q点坐标,不存在,请
说明理由。
图3
师生活动:学生小组讨论解决问题的方法,教师给予适当的指导,然后梳理解决问题的过程,教师用几何画板展示Q点不同的位置,让学生更直观地找到Q点的两种可能位置,然后由小组内同学合力整理出详细的过程书写,用小白板展示,教师和学生共同点评。
追问:在y轴上是否存在一点P,使得=,若存在,找出P的位置并求出P点的坐标。
师生活动:教师用几何画板展示找P点位置的动态图,学生观察说出思路,课后梳理解题过程。
设计意图:利用几何画板来突破学生空间想象能力的欠缺,让学生有能力在没有几何画板这个辅助工具的情况下能通过做平行线的方法找到点P或点Q的位置。
4、拓展提升,题型变式
问题5 在1题中,点G从A出发,以1个单位长度/秒的速度向右运动,运动时间为t秒,如图4,问t为何值时,=?求出t值和G点坐标。
图4
师生活动:学生回答思路,并用展台展示书写过程,教师顺势引导学生观察此题与前面所讲题目的区别是什么,把动态的问题转化成静态的图形,找到符合题意的G点位置,并通过计算求出G点坐标。
设计意图:动点问题一直是学生的难题,本题的设计就是想借助前面各题的铺垫来降低难度,消除学生的畏难情绪,用本节课中所学的方法来解决问题,提高学生的学习兴趣。
5、深入理解,拓展延伸
问题6 在4题中,过点C的直线CH平行于x轴,如图5,点R从C点出发,以0.5个单位长度/秒的速度向左运动,点G从A出发,以1个单位长度/秒的速度向右运动,运动时间t, 以O,C,G,R为顶点的四边形面积为S;
(1)用含t的式子表示S;
(2)当S=4时,求t的值及G、R的坐标。
图5
师生活动:学生独立完成,互相讲解。
设计意图:图形中有两个动点,为学生创设一个可以充分展现自己想象力的空间,然学生把动态图形转化成为静态图形进而解决问题。
6、回顾小结,归纳提升
教师和学生一起回顾本节课的所学内容,并请学生回答一下问题:
(1)平面直角坐标系中求图形面积的方法?
(2)过程书写的步骤是什么?
(3)如何找到满足条件的点的位置?
设计意图:通过小结,使学生梳理本节课所学内容,理解割补法求图形面积的方法,会用做平行线的方法找到满足条件的点的位置,体会数学结合的思想方法。
7、布置作业
习题练习
五、目标检测设计
如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足+=0
设计意图:本题主要考查学生对找P点的位置和用割补法表示图形面积,进而求出P点坐标的能力。
一、内容和内容解析
1、内容
会用割补法求平面直角坐标系中图形的面积
2、内容解析
“平面直角坐标系”是“数轴”的发展,使点与坐标的对应关系顺利实现了从一维到二维的过渡。“平面直角坐标系”的建立使得有序数对与平面内的点产生了一一对应,提供了用代数方法来解决几何问题的重要数学工具。
本章前几节课中,学生已经能够根据点的坐标表示出它到坐标轴的距离,并且能用平移的知识求出平行或垂直于坐标轴的线段长度。本节课先从平移体会求点坐标的方法,在此基础上又从已知图形面积求顶点坐标的方法,而后设定动点情景来求点的坐标,让学生体会用代数方法解决几何问题的过程。
在平面直角坐标系中不规则的图形,我们只能根据分割图形或者补充图形,使得它变成一个规则的图形来求解面积,构成几何图形的要素是点线面,这与平面直角坐标系中由点的坐标表示线段的长度进而求出图形的面积的研究方法是一致的,体现了数形结合的思想。
由以上分析,可以确定本节课的教学重点:用割补法求图形的面积。
二、目标和目标解析
1、目标
(1)会用割补法求平面直角坐标系中三角形和四边形的面积;
(2)体会从点坐标求线段长进而求出图形面积的过程;
2、目标解析
达成目标(1)的标志是:学生能把平面直角坐标系中倾斜三角形或者四边形通过作辅助线的方法分割或补充成水平或竖直的规则图形来求面积,一般情况下是补充成长方形或梯形。
达成目标(2)的标志是:学生在理解习题思路的基础上,能把已知条件中给出的点坐标转化成线段的长度,进而能够根据面积的大小求出点的坐标。
三、教学重难点
教学重难点是:理解用平行线来找与已知三角形同底等高的三角形,体会满足条件的点的位置的几种可能。
四、教学过程设计
1、复习引入
问题1 回顾已学内容,回答下列问题:
在平面直角坐标系中,如图1,将线段AB平移至线段CD,连接AC,BD。
(1)直接写出图中相等的线段和平行的线段 ;
(2)已知A(-3,0),B(-2,-2),C(0,)则D点坐标为; ;
师生活动:学生回答问题后,教师用几何画板展示动态图形,用平移的知识求出D点的坐标。
问题2 (3)在(2)中,若把“C(0,)”改为=5,其他条件不变,求C,D坐标。
图1
师生活动:学生回答,学生讲解,教师指出,由三角形面积可以求出三角形的边长,进而求出C点和D点的坐标。
设计意图:从学生熟悉的问题出发,让学生体会图形面积和点坐标之间的转化。
2、例题引领,掌握方法
问题3 在1题中,BD与x轴交点为E,与y轴交点为F,如图2,其他条件不变,若F(0,),求E点坐标。
图2
师生活动:学生回答,用实物展台展示过程的书写,教师引导强调可以先设E点的坐标,然后用图形面积之间的等量关系列出方程,进而求出E的坐标。
追问:如果已知E的坐标,如何求出F的坐标?
师生活动:学生思考后回答问题,教师总结,通性通法。
设计意图:让学生体会从点坐标求出线段长度进而求出图形面积的过程。
3、合作交流,探究新知
问题4 在2题中,若直线MN与x轴垂直且交于(-1,0),如图3,在MN上是否存在点Q,使=,其他条件不变,若存在,求出Q点坐标,不存在,请
说明理由。
图3
师生活动:学生小组讨论解决问题的方法,教师给予适当的指导,然后梳理解决问题的过程,教师用几何画板展示Q点不同的位置,让学生更直观地找到Q点的两种可能位置,然后由小组内同学合力整理出详细的过程书写,用小白板展示,教师和学生共同点评。
追问:在y轴上是否存在一点P,使得=,若存在,找出P的位置并求出P点的坐标。
师生活动:教师用几何画板展示找P点位置的动态图,学生观察说出思路,课后梳理解题过程。
设计意图:利用几何画板来突破学生空间想象能力的欠缺,让学生有能力在没有几何画板这个辅助工具的情况下能通过做平行线的方法找到点P或点Q的位置。
4、拓展提升,题型变式
问题5 在1题中,点G从A出发,以1个单位长度/秒的速度向右运动,运动时间为t秒,如图4,问t为何值时,=?求出t值和G点坐标。
图4
师生活动:学生回答思路,并用展台展示书写过程,教师顺势引导学生观察此题与前面所讲题目的区别是什么,把动态的问题转化成静态的图形,找到符合题意的G点位置,并通过计算求出G点坐标。
设计意图:动点问题一直是学生的难题,本题的设计就是想借助前面各题的铺垫来降低难度,消除学生的畏难情绪,用本节课中所学的方法来解决问题,提高学生的学习兴趣。
5、深入理解,拓展延伸
问题6 在4题中,过点C的直线CH平行于x轴,如图5,点R从C点出发,以0.5个单位长度/秒的速度向左运动,点G从A出发,以1个单位长度/秒的速度向右运动,运动时间t, 以O,C,G,R为顶点的四边形面积为S;
(1)用含t的式子表示S;
(2)当S=4时,求t的值及G、R的坐标。
图5
师生活动:学生独立完成,互相讲解。
设计意图:图形中有两个动点,为学生创设一个可以充分展现自己想象力的空间,然学生把动态图形转化成为静态图形进而解决问题。
6、回顾小结,归纳提升
教师和学生一起回顾本节课的所学内容,并请学生回答一下问题:
(1)平面直角坐标系中求图形面积的方法?
(2)过程书写的步骤是什么?
(3)如何找到满足条件的点的位置?
设计意图:通过小结,使学生梳理本节课所学内容,理解割补法求图形面积的方法,会用做平行线的方法找到满足条件的点的位置,体会数学结合的思想方法。
7、布置作业
习题练习
五、目标检测设计
如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足+=0
设计意图:本题主要考查学生对找P点的位置和用割补法表示图形面积,进而求出P点坐标的能力。
