2020-2021学年北师大版七年级数学下册第四章三角形单元测试题(Word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下册第四章三角形单元测试题(Word版含答案) | 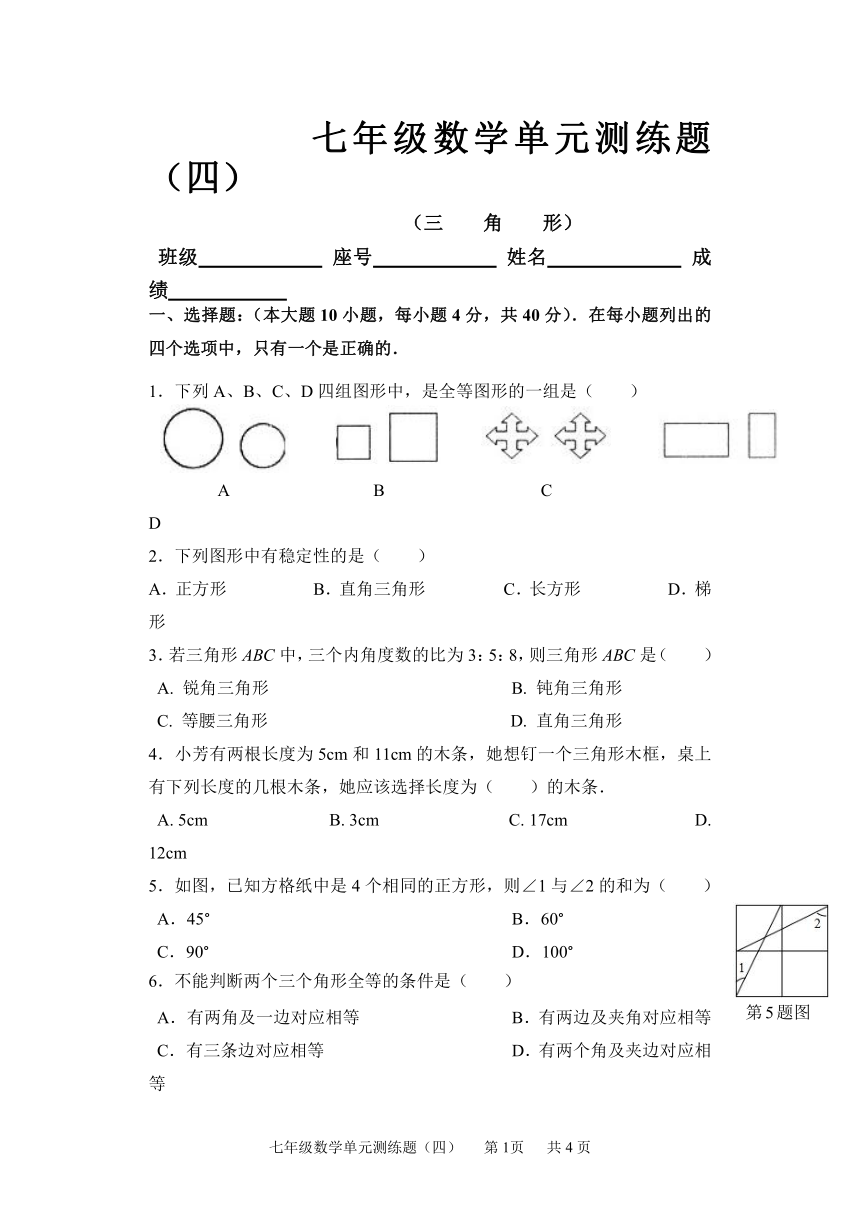 | |
| 格式 | docx | ||
| 文件大小 | 104.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 11:21:24 | ||
图片预览



文档简介
七年级数学单元测练题(四)
(三 角 形)
班级 座号 姓名 成绩
一、选择题:(本大题10小题,每小题4分,共40分).在每小题列出的四个选项中,只有一个是正确的.
1.下列A、B、C、D四组图形中,是全等图形的一组是( )
A B C D
2.下列图形中有稳定性的是( )
A.正方形 B.直角三角形 C.长方形 D.梯形
3.若三角形ABC中,三个内角度数的比为3:5:8,则三角形ABC是( )
A. 锐角三角形 B. 钝角三角形
C. 等腰三角形 D. 直角三角形
4.小芳有两根长度为5cm和11cm的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择长度为( )的木条.
A. 5cm B. 3cm C. 17cm D. 12cm
5.如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为( )
A.45° B.60°
C.90° D.100°
(
第5题图
)6.不能判断两个三个角形全等的条件是( )
A.有两角及一边对应相等 B.有两边及夹角对应相等
C.有三条边对应相等 D.有两个角及夹边对应相等
7.如图,△ABC中,D、E分别为BC、AD的中点,=20,
则阴影部分的面积是( )
A.5 B.10
(
第7题图
)C.18 D.1
8.如图,已知B,C,E三点在同一条直线上,∠A=∠DCE,
∠ACB=∠E,CD=AB.若BC=8,BE=1,则AC的长为( )
(
第8题图
)A.8 B.9 C.10 D.11
9.要测量圆形工件的外径,工人师傅设计了如右图所示的卡钳,O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则这个工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )
(
第9题图
)A. ASA B. AAS
C. SAS D. SSS
10.如图,∠ADB=∠ACB=90°,AC与BD相交于点O,且OA=OB,
下列结论:①AD=BC;②AC=BD;③∠CDA=∠CDB;④CD∥AB,
其中正确的有( )
(
第10题图
)A.1个 B.2个
C.3个 D.4个
二、填空题:(本大题6小题,每小题4分,共24分).请将下列各题的正确答案填在该题的横线上.
11.表示全等的符号“≌”是由“∽”和“=”两部分组成,其中“=”表示两个全等形的大小相等,
那么“∽”表示两个全等形的 相同.
(
第13题图
)12.如果三角形的三个内角分别是,那么满足的关系式
是 .
13.如图,黄芳不小心把一块三角形的玻璃摔成三块碎片,现要带其中
一块去配出与原来完全一样的玻璃,正确的办法是带第 块去配.
(
第14题图
)14.如图,BC∥EF,BC=BE,AB=FB,∠1=∠2,若∠1=55°,
则∠C的度数为 .
15.如图,点F、C在线段BE上,且∠1=∠2,BC=EF,
(
第15题图
)若要使△ABC≌△DEF,则还需补充一个条件是 ,
依据是 .
16.如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作
过点A的直线的垂线BD、CE,垂足分别为D、E,
(
第16题图
)若BD=2,CE=3,则DE= .
三、解答题:(本大题4小题,每小题9分,共36分).解答过程应写出文字说明、推理过程及演算步骤.
17.已知∠,线段a、b.请按下列步骤完成作图.(不需要写作法,保留作图痕迹)
(1)作∠PAQ=∠.
(2)在边AP上截取AB=a,在边AQ上截取AC=b.
(3)连接BC.
18.如图,点B、F、C、E在直线上(F、C之间不能直接测量),点A、D在异侧,
AB∥DE,∠A=∠D,测得AB=DE.
(1)说明:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
19.如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)说明:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
20.如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于E,点F在边AC上,连接DF.
(1)说明:AC=AE;
(2)若AC=8,AB=10,且△ABC的面积等于24,求DE的长;
(3)若CF=BE,直接写出线段AB,AF,EB的数量关系: .
(四)(三角形)
一、选择题: 1.C 2.B 3.D 4.D 5.C 6.A
7.A 8.B 9.C 10.C
二、填空题:11.形状 12. 13.2 14.55
15.AC=DF ,SAS 16.5
三、解答题: 17.略.
18.(1)证明:∵AB∥DE, ∴∠ABC=∠DEF,
在△ABC与△DEF中, ∠ABC=∠DEF AB=DE ∠A=∠D,
∴△ABC≌△DEF;
(2)∵△ABC≌△DEF, ∴BC=EF, ∴BF+FC=EC+FC,
∴BF=EC, ∵BE=10m,BF=3m, ∴FC=10-3-3=4m.
19.(1)∵AD∥BC ∴∠ADE=∠F ∵E是AB的中点 ∴AE=BE
又∵∠FEB=∠DEA ∴△ADE≌△BFE
(2)EG与DF的位置关系是EG⊥DF.
理由:∵∠GDF=∠ADE, ∠ADE=∠BFE ∴∠GDF=∠GFE ∴FG=GD
又∵由(1)△AED≌△BFE得:DE=EF,即GE为DF上的中线, ∴GE⊥DF
20.(1)∵∠C=90°,DE⊥AB ∴∠C=∠AED=90°,
在△ACD和△AED中,∠CAD=∠BAD ∠C=∠AED AD=AD,
∴△ACD≌△AED, ∴AC=AE.
(2)由(1)得:△ACD≌△AED, ∴DC=DE,
∵, ∴,
又∵AC=8,AB=10,且△ABC的面积等于24,∴24=×8×CD+×10×DE ∴DE=. (3)AB=AF+2EB.七年级数学单元测练题(四) 第2页 共4页
(三 角 形)
班级 座号 姓名 成绩
一、选择题:(本大题10小题,每小题4分,共40分).在每小题列出的四个选项中,只有一个是正确的.
1.下列A、B、C、D四组图形中,是全等图形的一组是( )
A B C D
2.下列图形中有稳定性的是( )
A.正方形 B.直角三角形 C.长方形 D.梯形
3.若三角形ABC中,三个内角度数的比为3:5:8,则三角形ABC是( )
A. 锐角三角形 B. 钝角三角形
C. 等腰三角形 D. 直角三角形
4.小芳有两根长度为5cm和11cm的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择长度为( )的木条.
A. 5cm B. 3cm C. 17cm D. 12cm
5.如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为( )
A.45° B.60°
C.90° D.100°
(
第5题图
)6.不能判断两个三个角形全等的条件是( )
A.有两角及一边对应相等 B.有两边及夹角对应相等
C.有三条边对应相等 D.有两个角及夹边对应相等
7.如图,△ABC中,D、E分别为BC、AD的中点,=20,
则阴影部分的面积是( )
A.5 B.10
(
第7题图
)C.18 D.1
8.如图,已知B,C,E三点在同一条直线上,∠A=∠DCE,
∠ACB=∠E,CD=AB.若BC=8,BE=1,则AC的长为( )
(
第8题图
)A.8 B.9 C.10 D.11
9.要测量圆形工件的外径,工人师傅设计了如右图所示的卡钳,O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则这个工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )
(
第9题图
)A. ASA B. AAS
C. SAS D. SSS
10.如图,∠ADB=∠ACB=90°,AC与BD相交于点O,且OA=OB,
下列结论:①AD=BC;②AC=BD;③∠CDA=∠CDB;④CD∥AB,
其中正确的有( )
(
第10题图
)A.1个 B.2个
C.3个 D.4个
二、填空题:(本大题6小题,每小题4分,共24分).请将下列各题的正确答案填在该题的横线上.
11.表示全等的符号“≌”是由“∽”和“=”两部分组成,其中“=”表示两个全等形的大小相等,
那么“∽”表示两个全等形的 相同.
(
第13题图
)12.如果三角形的三个内角分别是,那么满足的关系式
是 .
13.如图,黄芳不小心把一块三角形的玻璃摔成三块碎片,现要带其中
一块去配出与原来完全一样的玻璃,正确的办法是带第 块去配.
(
第14题图
)14.如图,BC∥EF,BC=BE,AB=FB,∠1=∠2,若∠1=55°,
则∠C的度数为 .
15.如图,点F、C在线段BE上,且∠1=∠2,BC=EF,
(
第15题图
)若要使△ABC≌△DEF,则还需补充一个条件是 ,
依据是 .
16.如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作
过点A的直线的垂线BD、CE,垂足分别为D、E,
(
第16题图
)若BD=2,CE=3,则DE= .
三、解答题:(本大题4小题,每小题9分,共36分).解答过程应写出文字说明、推理过程及演算步骤.
17.已知∠,线段a、b.请按下列步骤完成作图.(不需要写作法,保留作图痕迹)
(1)作∠PAQ=∠.
(2)在边AP上截取AB=a,在边AQ上截取AC=b.
(3)连接BC.
18.如图,点B、F、C、E在直线上(F、C之间不能直接测量),点A、D在异侧,
AB∥DE,∠A=∠D,测得AB=DE.
(1)说明:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
19.如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)说明:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
20.如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于E,点F在边AC上,连接DF.
(1)说明:AC=AE;
(2)若AC=8,AB=10,且△ABC的面积等于24,求DE的长;
(3)若CF=BE,直接写出线段AB,AF,EB的数量关系: .
(四)(三角形)
一、选择题: 1.C 2.B 3.D 4.D 5.C 6.A
7.A 8.B 9.C 10.C
二、填空题:11.形状 12. 13.2 14.55
15.AC=DF ,SAS 16.5
三、解答题: 17.略.
18.(1)证明:∵AB∥DE, ∴∠ABC=∠DEF,
在△ABC与△DEF中, ∠ABC=∠DEF AB=DE ∠A=∠D,
∴△ABC≌△DEF;
(2)∵△ABC≌△DEF, ∴BC=EF, ∴BF+FC=EC+FC,
∴BF=EC, ∵BE=10m,BF=3m, ∴FC=10-3-3=4m.
19.(1)∵AD∥BC ∴∠ADE=∠F ∵E是AB的中点 ∴AE=BE
又∵∠FEB=∠DEA ∴△ADE≌△BFE
(2)EG与DF的位置关系是EG⊥DF.
理由:∵∠GDF=∠ADE, ∠ADE=∠BFE ∴∠GDF=∠GFE ∴FG=GD
又∵由(1)△AED≌△BFE得:DE=EF,即GE为DF上的中线, ∴GE⊥DF
20.(1)∵∠C=90°,DE⊥AB ∴∠C=∠AED=90°,
在△ACD和△AED中,∠CAD=∠BAD ∠C=∠AED AD=AD,
∴△ACD≌△AED, ∴AC=AE.
(2)由(1)得:△ACD≌△AED, ∴DC=DE,
∵, ∴,
又∵AC=8,AB=10,且△ABC的面积等于24,∴24=×8×CD+×10×DE ∴DE=. (3)AB=AF+2EB.七年级数学单元测练题(四) 第2页 共4页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
