2.5用三种方法表示二次函数
图片预览


文档简介
课件11张PPT。用三种方式表示二次函数学习目标:
1.能够分析和表示变量之间的二次函数关系,并解决用二次 函数所表示的问题.
2.能够根据二次函数的不同表示方式,从不同侧面对函数 性质进行研究.
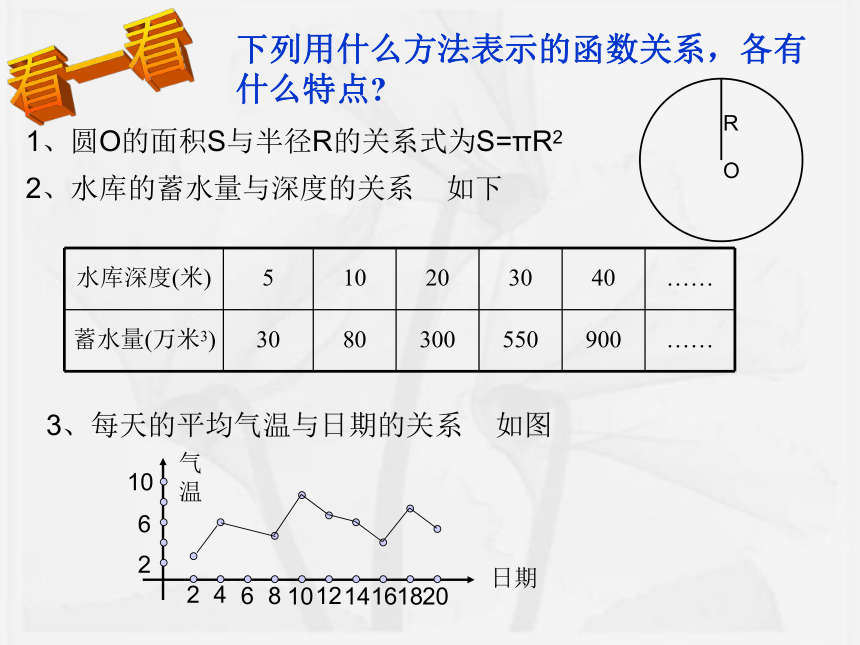
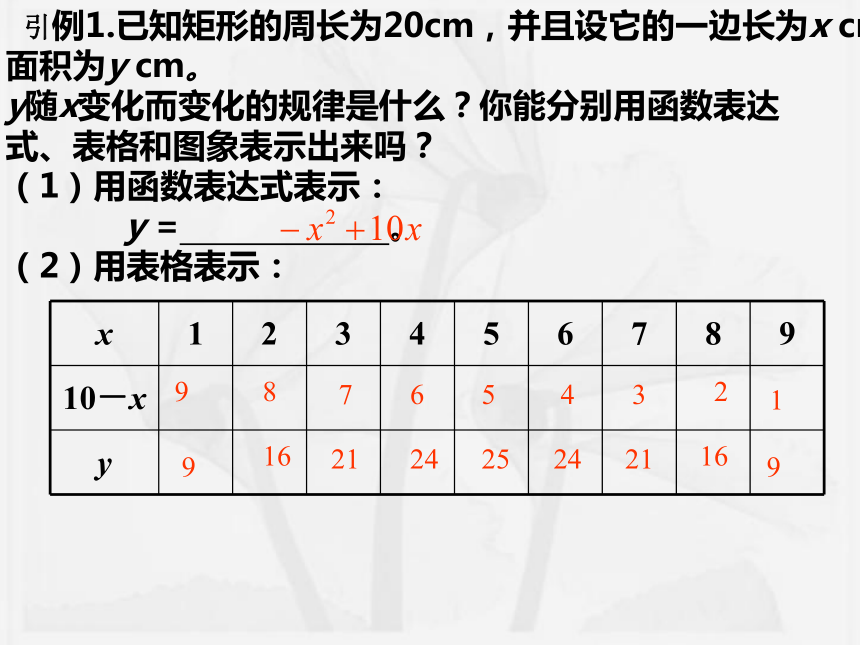
3.经历用三种方式表示变量之间二次函数关系的过程,体会三种方式之间的联系与各自不同的特点.看一看1、圆O的面积S与半径R的关系式为S=πR23、每天的平均气温与日期的关系 如图2、水库的蓄水量与深度的关系 如下下列用什么方法表示的函数关系,各有什么特点? 引例1.已知矩形的周长为20cm,并且设它的一边长为x cm,
面积为y cm。
y随x变化而变化的规律是什么?你能分别用函数表达
式、表格和图象表示出来吗?
(1)用函数表达式表示:
y = 。
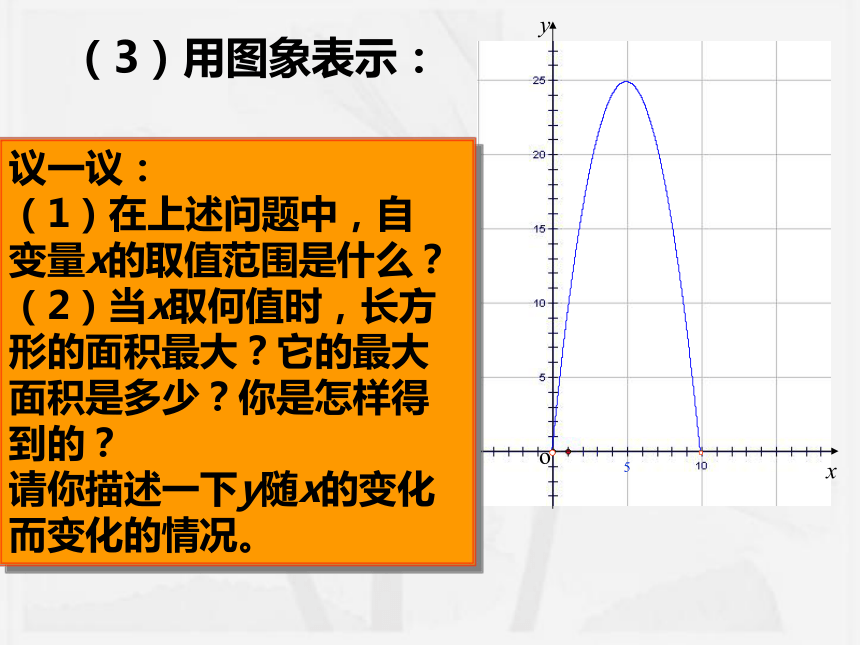
(2)用表格表示:525(3)用图象表示:议一议:
(1)在上述问题中,自
变量x的取值范围是什么?
(2)当x取何值时,长方
形的面积最大?它的最大面积是多少?你是怎样得到的?
请你描述一下y随x的变化而变化的情况。做一做:
两个数相差2,设其中较大一个数为x ,那么它们的积y 是
如何随x的变化而变化的?你能分别用函数表达式、表格和图
象表示这种变化吗?
1、用函数表达式表示:y= 。
2、用表格表示: 3、用图象表示:4、根据以上三种表示方式回答下列问题:
(1)自变量x 的取值范围是什么?
(2)图象的对称轴和顶点坐标分别是什么?
(3)如何描述y随x的变化而变化的情况?
(4)你是分别通过哪种表示方式回答
上面三个问题的?议一议函数的表格表示可以清楚、直接地表示出变量之间
的数值对应关系;
函数的图象表示可以直观地表示出函数的变化过程
和变化趋势;
函数的表达式可以比较全面、完整、简洁地表示出
变量之间的关系,
这三种表示方式各自有各自的优点,它们服务于不同的需要.
它们的联系是三种方式可以互化,由表达式可转化为表格和图象表示,每一种方式都可转化为另两种方式表示.二次函数的三种表示方式有什么特点?它们之间有什么联系?三种表示方式必须考虑自变量的取值范围 !三种表示方式的关系流程图表格表示图像表示表达式(一)由函数图象上的点的坐标用待定系数法求函数解析式求下列条件下的二次函数的解析式:
1.已知一个二次函数的图象经过点(0,0),
(1,﹣3),(2,﹣8)。
2.已知二次函数的图象的顶点坐标为(-2,-3), 且图象过点(-3,-2)。
练习:
1.图象经过三点A(0,1), B(1,-2), C(2,-1)
2、抛物线的顶点坐标是(6,-2),且与X轴的一个
交点的横坐标是8。
(二)是根据实际问题的条件或图形的性质确定函数的关系式。例:行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑动一段距离才停止,这段距离称为“刹车距离”.为了测定某种型号汽车的刹车性能(车速不超过130km/h),对这种汽车进行测试,测得数据如下表:
(1)以车速为x轴,刹车距离为y轴,建立坐标系,描出这些数据所表示的点,并用平滑曲线连接这些点,得到函数的大致图象;
(2)观察图象,估计该函数的类型,并确定一个满足这些数据的函数表达式;
(3)该型号汽车在国道上发生了一次交通事故,现测得刹车距离为26.4m,问在事故发生时,汽车是超速行驶还是正常行驶,请说明理由.小结:1.本节学习了函数的三种表示方式:解析法;图象法。列表法;2.解析法能定量地反映两个变量之间的对应关系的规律;3.列表法能表达出某些自变量对应的具体的函数值关系。对于对应关系不容易找出规律的,用列表法较容易表达清楚。4.图象法能形象地反映出函数的变化趋势。它比解析法和列表法更直观和形象。 5.在解决问题时,要根据具体情况的需要选择某种表示方
法,表达实际的对应关系。
1.能够分析和表示变量之间的二次函数关系,并解决用二次 函数所表示的问题.
2.能够根据二次函数的不同表示方式,从不同侧面对函数 性质进行研究.
3.经历用三种方式表示变量之间二次函数关系的过程,体会三种方式之间的联系与各自不同的特点.看一看1、圆O的面积S与半径R的关系式为S=πR23、每天的平均气温与日期的关系 如图2、水库的蓄水量与深度的关系 如下下列用什么方法表示的函数关系,各有什么特点? 引例1.已知矩形的周长为20cm,并且设它的一边长为x cm,
面积为y cm。
y随x变化而变化的规律是什么?你能分别用函数表达
式、表格和图象表示出来吗?
(1)用函数表达式表示:
y = 。
(2)用表格表示:525(3)用图象表示:议一议:
(1)在上述问题中,自
变量x的取值范围是什么?
(2)当x取何值时,长方
形的面积最大?它的最大面积是多少?你是怎样得到的?
请你描述一下y随x的变化而变化的情况。做一做:
两个数相差2,设其中较大一个数为x ,那么它们的积y 是
如何随x的变化而变化的?你能分别用函数表达式、表格和图
象表示这种变化吗?
1、用函数表达式表示:y= 。
2、用表格表示: 3、用图象表示:4、根据以上三种表示方式回答下列问题:
(1)自变量x 的取值范围是什么?
(2)图象的对称轴和顶点坐标分别是什么?
(3)如何描述y随x的变化而变化的情况?
(4)你是分别通过哪种表示方式回答
上面三个问题的?议一议函数的表格表示可以清楚、直接地表示出变量之间
的数值对应关系;
函数的图象表示可以直观地表示出函数的变化过程
和变化趋势;
函数的表达式可以比较全面、完整、简洁地表示出
变量之间的关系,
这三种表示方式各自有各自的优点,它们服务于不同的需要.
它们的联系是三种方式可以互化,由表达式可转化为表格和图象表示,每一种方式都可转化为另两种方式表示.二次函数的三种表示方式有什么特点?它们之间有什么联系?三种表示方式必须考虑自变量的取值范围 !三种表示方式的关系流程图表格表示图像表示表达式(一)由函数图象上的点的坐标用待定系数法求函数解析式求下列条件下的二次函数的解析式:
1.已知一个二次函数的图象经过点(0,0),
(1,﹣3),(2,﹣8)。
2.已知二次函数的图象的顶点坐标为(-2,-3), 且图象过点(-3,-2)。
练习:
1.图象经过三点A(0,1), B(1,-2), C(2,-1)
2、抛物线的顶点坐标是(6,-2),且与X轴的一个
交点的横坐标是8。
(二)是根据实际问题的条件或图形的性质确定函数的关系式。例:行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑动一段距离才停止,这段距离称为“刹车距离”.为了测定某种型号汽车的刹车性能(车速不超过130km/h),对这种汽车进行测试,测得数据如下表:
(1)以车速为x轴,刹车距离为y轴,建立坐标系,描出这些数据所表示的点,并用平滑曲线连接这些点,得到函数的大致图象;
(2)观察图象,估计该函数的类型,并确定一个满足这些数据的函数表达式;
(3)该型号汽车在国道上发生了一次交通事故,现测得刹车距离为26.4m,问在事故发生时,汽车是超速行驶还是正常行驶,请说明理由.小结:1.本节学习了函数的三种表示方式:解析法;图象法。列表法;2.解析法能定量地反映两个变量之间的对应关系的规律;3.列表法能表达出某些自变量对应的具体的函数值关系。对于对应关系不容易找出规律的,用列表法较容易表达清楚。4.图象法能形象地反映出函数的变化趋势。它比解析法和列表法更直观和形象。 5.在解决问题时,要根据具体情况的需要选择某种表示方
法,表达实际的对应关系。
