2021-2022学年苏科版八年级数学下册9.4矩形、菱形、正方形解答题专题训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学下册9.4矩形、菱形、正方形解答题专题训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 309.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 12:08:33 | ||
图片预览


文档简介
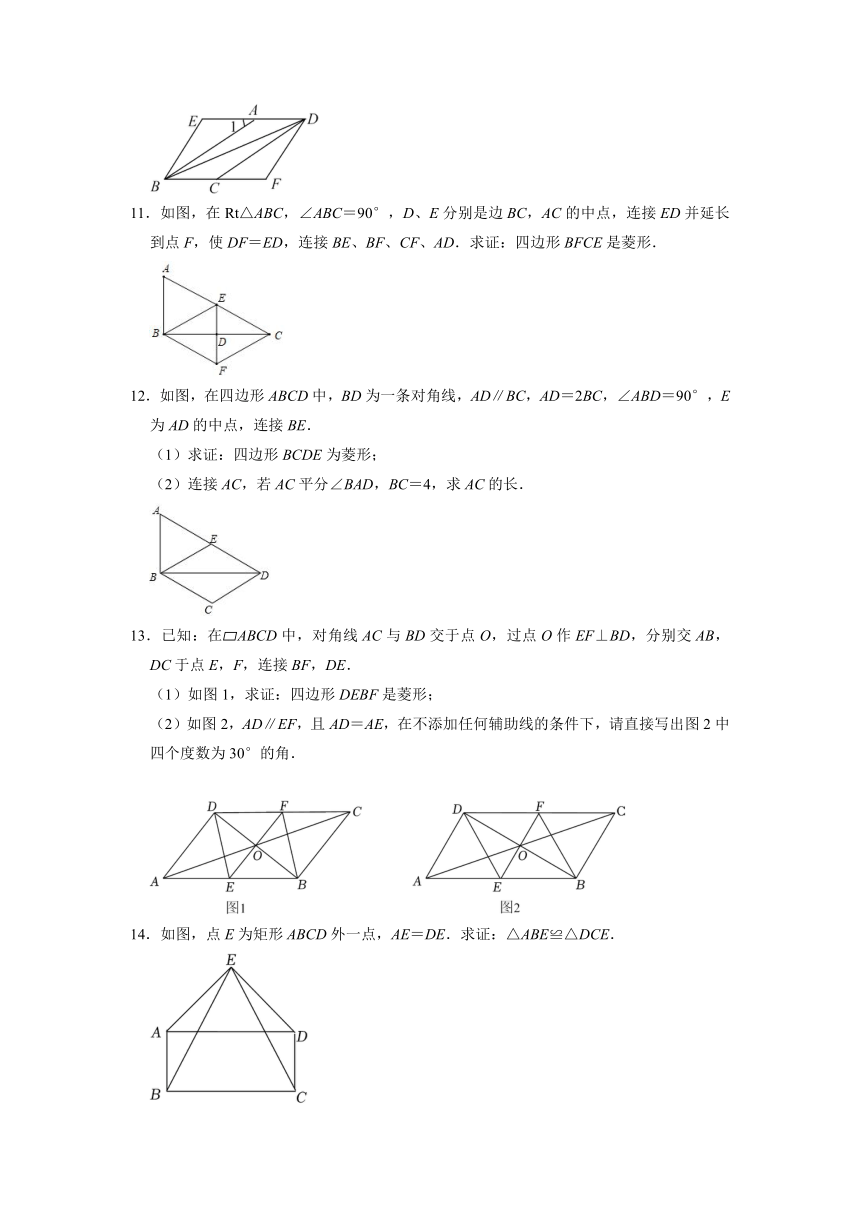
2021-2022学年苏科版八年级数学下册《9-4矩形、菱形、正方形》
解答题专题训练(附答案)
1.如图,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E、F分别为边AB、AC的中点,当AD=6时,BC边上存在一点Q,使∠EQF=90°,求此时BQ的长.
2.如图,菱形ABCD的对角线相交于点O,∠BAD=60°,菱形ABCD的周长为24.
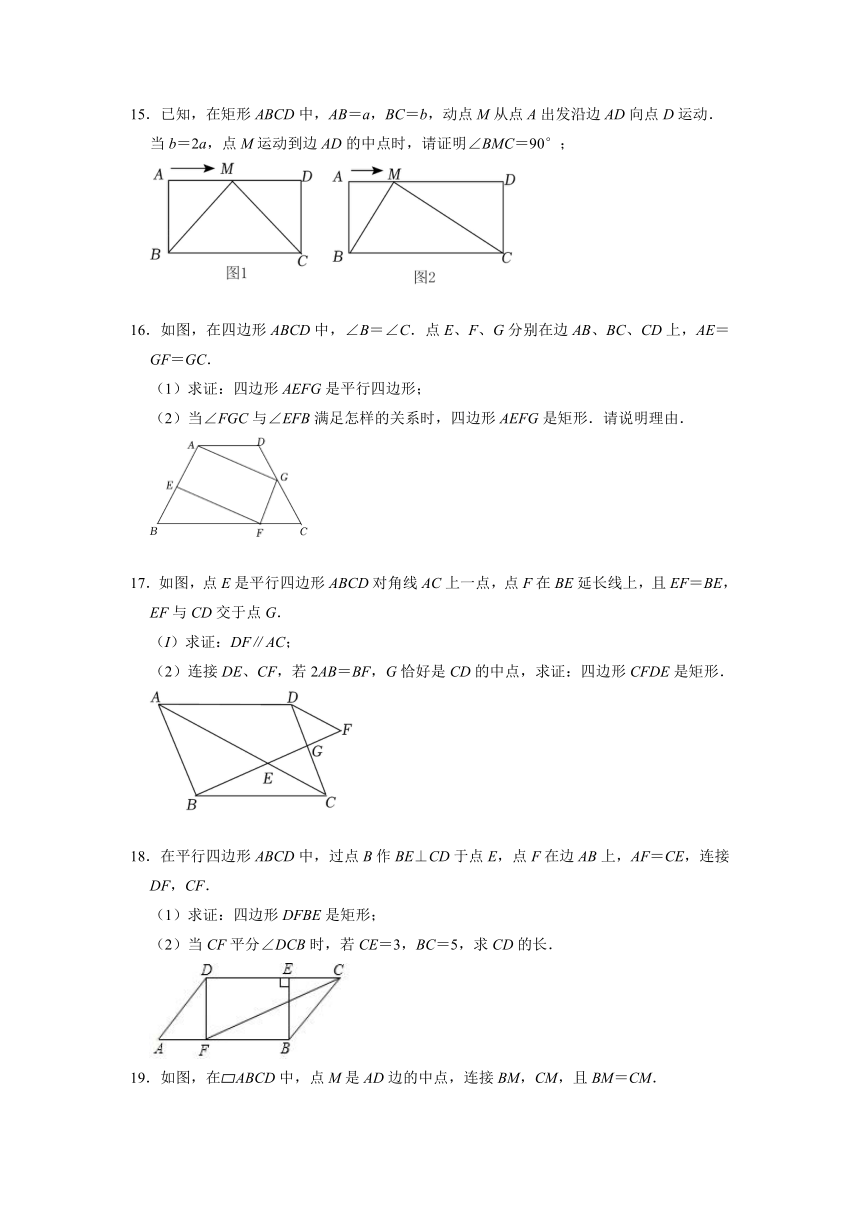
(1)求对角线BD的长;
(2)求菱形ABCD的面积.
3.如图,四边形ABCD是平行四边形,且对角线AC,BD交于点O,BD=2AB,AE∥BD,OE∥AB.求证:四边形ABOE是菱形.
4.如图,在Rt△ABC中,∠ACB=90°,CD、CE三等分∠ACB,且CD是AB边的中线,CE是BD边的中线,当DE=2时,求AC的长.
5.如图,已知在△ABC中,∠A=60°,点D是BC的中点,CE⊥AB,BF⊥AC,垂足分别为E、F,连接DE、DF、EF.
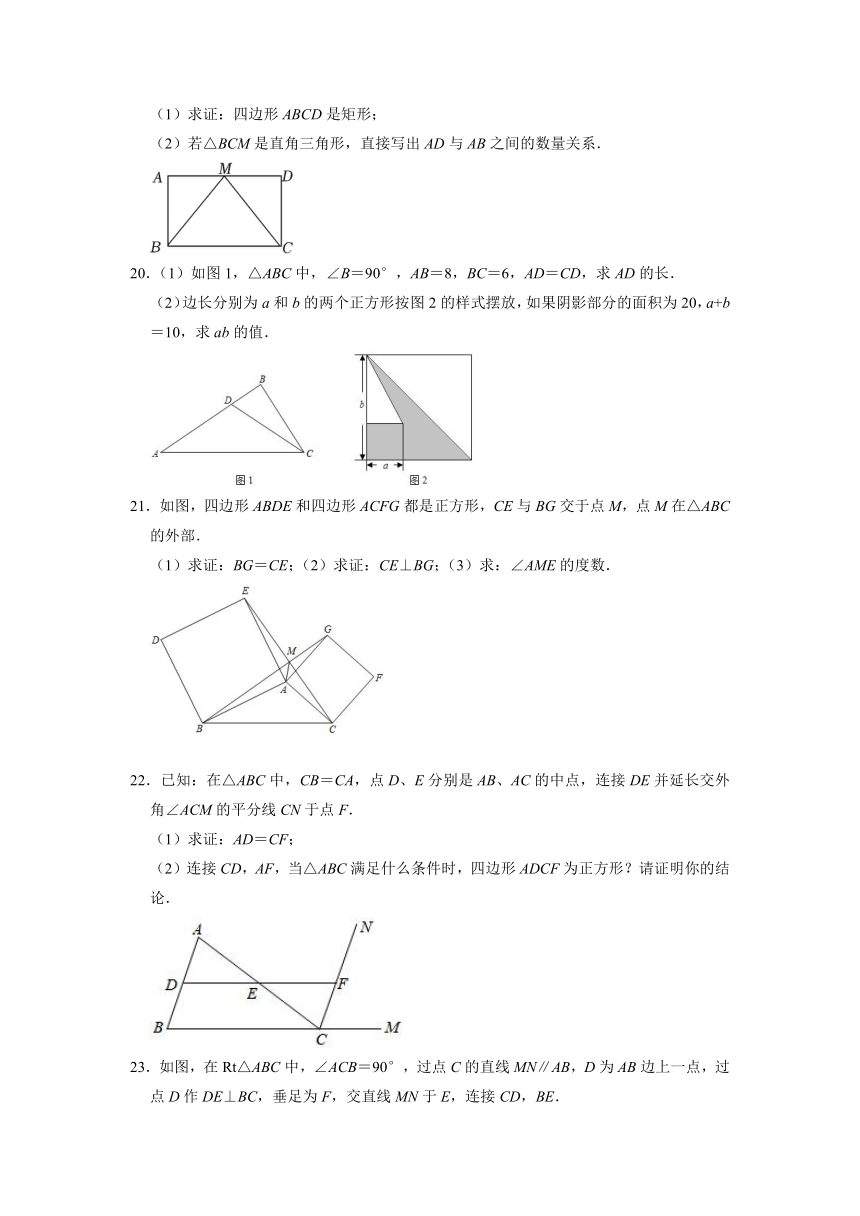
求证:△DEF为等边三角形.
6.求证:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.在探究过程中,老师发现班上的学生有两种不同辅助线添法,如图,在△ABC中,∠ACB=90°.
甲同学:以B为圆心,以BA长为半径作弧,交BC延长线于D,连接AD.
乙同学:以B为圆心,以BC长为半径作弧,交BA于D,连接CD.
请你选择上述一种做法进行证明.(要求写出已知,求证,证明过程)
7.如图,在菱形ABCD中,点E,F分别是边AB和BC上的点,且BE=BF.求证:∠DEF=∠DFE.
8.如图,在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F.
(1)求证:BE=DF.
(2)当∠BAD=110°时,求∠EAF的度数.
9.在菱形ABCD中,∠BAD=60°,点E、F分别在边AB、AD上,且AE=DF,BF与DE交于点G.
(1)如图①,连接BD.求证:△ADE≌△DBF;
(2)如图②,连接CG.求证:BG+DG=CG.
10.如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF.
(1)求证:△ABE≌△CDF;
(2)连接BD,若∠1=32°,∠ADB=22°,请直接写出当∠ABE= °时,四边形BFDE是菱形.
11.如图,在Rt△ABC,∠ABC=90°,D、E分别是边BC,AC的中点,连接ED并延长到点F,使DF=ED,连接BE、BF、CF、AD.求证:四边形BFCE是菱形.
12.如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=4,求AC的长.
13.已知:在 ABCD中,对角线AC与BD交于点O,过点O作EF⊥BD,分别交AB,DC于点E,F,连接BF,DE.
(1)如图1,求证:四边形DEBF是菱形;
(2)如图2,AD∥EF,且AD=AE,在不添加任何辅助线的条件下,请直接写出图2中四个度数为30°的角.
14.如图,点E为矩形ABCD外一点,AE=DE.求证:△ABE≌△DCE.
15.已知,在矩形ABCD中,AB=a,BC=b,动点M从点A出发沿边AD向点D运动.
当b=2a,点M运动到边AD的中点时,请证明∠BMC=90°;
16.如图,在四边形ABCD中,∠B=∠C.点E、F、G分别在边AB、BC、CD上,AE=GF=GC.
(1)求证:四边形AEFG是平行四边形;
(2)当∠FGC与∠EFB满足怎样的关系时,四边形AEFG是矩形.请说明理由.
17.如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G.
(I)求证:DF∥AC;
(2)连接DE、CF,若2AB=BF,G恰好是CD的中点,求证:四边形CFDE是矩形.
18.在平行四边形ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接DF,CF.
(1)求证:四边形DFBE是矩形;
(2)当CF平分∠DCB时,若CE=3,BC=5,求CD的长.
19.如图,在 ABCD中,点M是AD边的中点,连接BM,CM,且BM=CM.
(1)求证:四边形ABCD是矩形;
(2)若△BCM是直角三角形,直接写出AD与AB之间的数量关系.
20.(1)如图1,△ABC中,∠B=90°,AB=8,BC=6,AD=CD,求AD的长.
(2)边长分别为a和b的两个正方形按图2的样式摆放,如果阴影部分的面积为20,a+b=10,求ab的值.
21.如图,四边形ABDE和四边形ACFG都是正方形,CE与BG交于点M,点M在△ABC的外部.
(1)求证:BG=CE;(2)求证:CE⊥BG;(3)求:∠AME的度数.
22.已知:在△ABC中,CB=CA,点D、E分别是AB、AC的中点,连接DE并延长交外角∠ACM的平分线CN于点F.
(1)求证:AD=CF;
(2)连接CD,AF,当△ABC满足什么条件时,四边形ADCF为正方形?请证明你的结论.
23.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)
24.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OD的长.
25.如图,在正方形ABCD中,E,F,G,H分别在它的四条边上,且AE=BF=CG=DH.四边形EFGH是什么特殊四边形?你是如何判断的?
参考答案
1.解:∵E、F分别为边AB、AC的中点,
∴EF∥BC,EF=BC,
∵BC=12,
∴EF=6,
取EF的中点O,过点O作OQ⊥BC与Q,过点E作EG⊥BC于G,
∵AD是BC边上的高,AD=6,
∴OQ=EG=×6=3,
∴点Q即为所求的使∠EQF=90°的点,
∵EF∥BC,EG∥OQ,OE=OQ=3,
∴四边形OEQG是正方形,
∴GQ=OQ=3,
∵点E是AB的中点,
∴EG是△ABD的中位线,
∴EG=AD=3,
∵∠ABC=60°,
∴BG=EG=×3=,
∴BQ=BG+GQ=3+.
2.解:(1)∵四边形ABCD是菱形,周长为24,
∴AB=BC=CD=AD=6,AC⊥BD,OB=OD=BD,OA=OC=AC,∠BAO=∠BAD=×60°=30°,
∴∠AOB=90°,
∴OB=AB=3,
∴BD=2OB=6;
(2)由(1)得:BD=6,AB=6,OB=3,∠AOB=90°,
∴OA===3,
∴AC=2OA=6,
∴菱形ABCD的面积=AC×BD=×6×6=18.
3.证明:∵四边形ABCD是平行四边形,
∴OB=OD=BD,
∵BD=2AB,
∴AB=OB,
∵AE∥BD,OE∥AB,
∴四边形ABOE是平行四边形,
∵AB=OB,
∴四边形ABOE是菱形.
4.解:∵∠ACB=90°,CD、CE三等分∠ACB,
∴∠ACD=∠DCE=∠BCE=30°,
∵CD是AB边的中线,
∴AD=CD=BD=AB,
∴∠A=∠ACD=30°,
∵CE是BD边的中线,DE=2,
∴BD=2DE=4,
∴AB=8,
∴BC=AB=4,
∴AC==4,
故AC的长为4.
5.证明:∵CE⊥AB,BF⊥AC,
∴∠AEC=∠BEC=∠AFB=∠BFC=90°,
∵∠A=60°,
∴∠ABF=∠ACE=30°,
∴∠FBC+∠ECB=180°﹣∠A﹣∠ABF﹣∠ACE=60°,
∵点D是BC的中点,
∴DE=CD=BC,DF=BD=BC,
∴∠DEC=∠DCE,∠DBF=∠DFB,DE=DF,
∵∠BDE=∠DEC+∠DCE=2∠DCE,
∠CDF=∠DBF+∠DFB=2∠DBF,
∴∠BDE+∠CDF=2∠DBF+2∠DCE=2×60°=120°,
∴∠EDF=60°,
∴△DEF为等边三角形.
6.解:甲同学:如图1,已知在△ABC中,∠ACB=90°,∠BAC=30°,
求证:BC=AB,
证明:以B为圆心,以BA长为半径作弧,交BC延长线于D,连接AD,
则AB=BD,
∵∠ACB=90°,∠BAC=30°,
∴∠B=60°,
∴△ABD是等边三角形,
∴AD=AB,
∴BC=CD=BD=AB;
乙同学:如图2,已知在△ABC中,∠ACB=90°,∠BAC=30°,
求证:BC=AB,
证明:以B为圆心,以BC长为半径作弧,交BA于D,连接CD,
则BD=BC,
∵∠ACB=90°,∠BAC=30°,
∴∠B=60°,
∴△BCD是等边三角形,
∴CD=BD=BC,∠BDC=∠BCD=60°,
∴∠ACD=30°,
∴∠A=∠ACD,
∴AD=CD=BD=BC=AB.
7.证明:∵四边形ABCD是菱形,
∴∠A=∠C,AB=CB,AD=DC,
∵BE=BF,
∴AE=CF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴DE=DF,
∴∠DEF=∠DFE.
8.(1)证明:∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD,
∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(AAS),
∴BE=DF;
(2)解:∵四边形ABCD是菱形,
∴AD∥BC,
∴∠BAD+∠B=180°,
∵∠BAD=110°,
∴∠B=70°
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=20°,
∴∠DAF=20°,
∴∠EAF=∠BAD﹣∠BAE﹣∠DAF=110°﹣20°﹣20°=70°.
9.证明:(1)∵四边形ABCD是菱形,∠BAD=60°,
∴AB=BC=CD=AD,∠C=∠BAD=60°,
∴△ABD和△CBD都是等边三角形,
∴AD=DB,∠BDF=∠DAE=60°,
在△ADE和△DBF中,
,
∴△ADE≌△DBF(SAS);
(2)如图②,延长GB到点H,使BH=DG,连接CH、BD,
由(1)知△ADE≌△DBF,△CBD是等边三角形,
∴∠ADE=∠DBF,∠CBD=∠BCD=60°,
∴∠DBF+∠CBH=180°﹣∠CBD=120°,
∵四边形ABCD是菱形,∠BAD=60°,
∴BC=CD,∠ADC=180°﹣∠BAD=120°,
∴∠ADE+∠CDG=120°,
∴∠CBH=∠CDG,
在△CBH和△CDG中,
,
∴△CBH≌△CDG(SAS),
∴CH=CG,∠BCH=∠DCG,
∵∠BCD=∠DCG+∠BCG=60°,
∴∠BCH+∠BCG=60°,
即∠GCH=60°,
∴△CGH是等边三角形,
∴GH=CG,
∵GH=BG+BH=BG+DG,
∴BG+DG=CG.
10.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠BCD,
∴∠1=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:当∠ABE=12°时,四边形BFDE是菱形,理由如下:
∵△ABE≌△CDF,
∴BE=DF,AE=CF,
∴BF=DE,
∴四边形BFDE是平行四边形,
∵∠1=32°,∠ADB=22°,
∴∠ABD=∠1﹣∠ADB=10°,
∵∠ABE=12°,
∴∠DBE=∠ABD+∠ABE=22°,
∴∠DBE=∠ADB=22°,
∴BE=DE,
∴平行四边形BFDE是菱形,
故答案为:12.
11.证明:∵D是边BC的中点,
∴BD=CD,
∵DF=ED,
∴四边形BFCE是平行四边形,
在Rt△ABC中,∠ABC=90°,E是边AC的中点,
∴BE=CE,
∴四边形BFCE是菱形.
12.(1)证明:∵AD=2BC,E为AD的中点,
∴DE=BC,
∵AD∥BC,
∴四边形BCDE是平行四边形,
∵∠ABD=90°,AE=DE,
∴BE=DE,
∴四边形BCDE是菱形.
(2)解:连接AC.
∵AD∥BC,AC平分∠BAD,
∴∠BAC=∠DAC=∠BCA,
∴AB=BC=4,
∵AD=2BC=8,
∴sin∠ADB=,
∴∠ADB=30°,
∴∠DAC=30°,∠ADC=60°,
∴∠ACD=90°,
在Rt△ACD中,∵AD=8,
∴CD=4,AC=4.
13.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠OBE=∠ODF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA),
∴BE=DF,
∵BE∥DF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形;
(2)解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AD∥EF,
∴四边形ADFE是平行四边形,
∴AE=DF,
由(1)得:四边形DEBF是菱形,
∴DE=DF=BE,
∴AD=DE,
∵AD=AE,
∴AD=AE=DE,
∴△ADE是等边三角形,
∴∠AED=60°,
∵DE=BE,
∴∠EDB=∠EBD=∠AED=30°,
同理:∠FDB=∠FBD=30°,
即图2中四个度数为30°的角为∠EDB、∠EBD、∠FDB、∠FBD.
14.证明:∵AE=DE.
∴∠EAD=∠EDA,
∵四边形ABCD是矩形,
∴AB=CD,∠BAD=∠CDA,
∴∠EAD+∠BAD=∠EDA+∠CDA,
∴∠EAB=∠EDC,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS).
15.(1)证明:∵b=2a,点M是AD的中点,
∴AB=AM=MD=DC=a,
在矩形ABCD中,∠A=∠D=90°,
∴∠AMB=∠DMC=45°,
∴∠BMC=90°.
16.(1)证明:在四边形ABCD中,∠B=∠C,
∵GF=GC,
∴∠C=∠GFC,∠B=∠GFC,
∴AB∥GF,
即AE∥GF,
∵AE=GF,
∴四边形AEFG是平行四边形.
(2)解:当∠FGC=2∠EFB时,四边形AEFG是矩形,
理由:∵∠FGC+∠GFC+∠C=180o,∠GFC=∠C,∠FGC=2∠EFB,
∴2∠GFC+2∠EFB=180°,
∴∠BFE+∠GFC=90°.
∴∠EFG=90°.
∵四边形AEFG是平行四边形,
∴四边形AEFG是矩形.
17.(1)证明:连接BD,交AC于点O,如图所示:
∵四边形ABCD是平行四边形,
∴BO=DO,
∵BE=EF,
∴OE是△BDF的中位线,
∴OE∥DF,
即DF∥AC;
(2)证明:如图所示:
由(1)得:DF∥AC,
∴∠DFG=∠CEG,∠GDF=∠GCE,
∵G是CD的中点,
∴DG=CG,
在△DFG和△CEG中,
,
∴△DFG≌△CEG(AAS),
∴FG=EG,
∴四边形CFDE是平行四边形,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵2AB=BF,
∴2CD=BF,
又∵EF=BE,
∴CD=EF,
∴平行四边形CFDE是矩形.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED.
∴四边形DFBE是平行四边形,
∵BE⊥CD,
∴∠BED=90°.
∴四边形DFBE是矩形;
(2)解:由(1)得:四边形DFBE是矩形,
∴DE=BF,
∵CF平分∠DCB,
∴∠DCF=∠BCF,
∵AB∥CD,
∴∠DCF=∠CFB,
∴∠BCF=∠CFB,
∴BF=BC=5,
∴DE=BF=5,
∴CD=DE+CE=5+3=8.
19.(1)证明:∵点M是AD边的中点,
∴AM=DM,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥CD,
在△ABM和△DCM中,
,
∴△ABM≌△DCM(SSS),
∴∠A=∠D,
∵AB∥CD,
∴∠A+∠D=180°,
∴∠A=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
(2)解:AD与AB之间的数量关系:AD=2AB,理由如下:
∵△BCM是直角三角形,BM=CM,
∴△BCM是等腰直角三角形,
∴∠MBC=45°,
由(1)得:四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠AMB=∠MBC=45°,
∴△ABM是等腰直角三角形,
∴AB=AM,
∵点M是AD边的中点,
∴AD=2AM
∴AD=2AB.
20.解:(1)设AD=CD=x,则BD=8﹣x,
∵∠B=90°,BD=8﹣x,BC=6,CD=x,
∴(8﹣x)2+62=x2,
解得x=,
即AD的长为;
(2)由图可得,
b2﹣a(b﹣a)=20,
化简,得:a2﹣ab+b2=40①,
∵a+b=10,
∴(a+b)2=100,
∴a2+2ab+b2=100②,
②﹣①,得
3ab=60,
解得ab=20.
21.(1)证明:在正方形ABDE和ACFG中,AB=AE,AC=AG,∠BAE=∠CAG=90°,
∴∠BAE+∠BAC=∠CAG+∠BAC,
即∠CAE=∠BAG,
∵在△ABG和△AEC中,
,
∴△ABG≌△AEC(SAS),
∴BG=CE;
(2)证明:设BG、CE相交于点N,
∵△ABG≌△AEC,
∴∠ACE=∠AGB,
∵∠NCF+∠NGF=∠ACF+∠AGF=90°+90°=180°,
∴∠CNG=360°﹣(∠NCF+∠NGF+∠F)=360°﹣(180°+90°)=90°,
∴BG⊥CE;
(3)解:过A作BG,CE的垂线段交于点P,Q,
∵△ABG≌△AEC,
∴AP=AQ,
∴AM是角平分线,
∴∠AMC=45°,
∴∠AME=135°.
22.(1)证明:∵CB=CA,
∴∠A=∠B,
∵∠ACM=∠A+∠B,
∴∠A=ACM,
∵CN平分∠ACM,
∴∠ACF=ACM,
∴∠A=∠ACF,
∵E是AC的中点,
∴AE=CE,
在△ADE与△CFE中,
,
∴△ADE≌△CFE(ASA),
∴AD=CF;
(2)解:当△ABC满足∠ACB=90°,四边形ADCF是正方形,
证明:连接CD,AF,
∵AC=BC,∠ACB=90°,
∴△ACB是等腰直角三角形,
∴∠BAC=45°,
∵CN平分∠ACM,
∴∠ACF=ACM=45°,
∴∠DAC=∠ACF,
∴AD∥CF,
由(1)知AD=CF,
∴四边形ADCF是平行四边形,
∵点D是AB的中点,
∴AD=CD,
∴∠ACD=∠CAD=45°,
∴∠DCF=90°,
∴矩形ADCF是正方形.
23.(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
(3)解:当∠A=45°时,四边形BECD是正方形,
理由:∵∠ACB=90°,
∴∠ABC=45°,
由(2)可知,四边形BECD是菱形,
∴∠ABC=∠CBE=45°,
∴∠DBE=90°,
∴四边形BECD是正方形.
24.(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)∵四边形ABEF是正方形,
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∵AD=AE,
∴AD﹣AF=AE﹣AG,
即DF=EG,
在△DFO和△EGO中,,
∴△DFO≌△EGO(AAS),
∴FO=GO,FD=EG
∵∠DAE=∠AEF=45°,∠AFE=∠AGD=90°,
∴DF=FO=OG=EG,
∴DO=OF=OG,
∴DG=DO+OG=OG+OG=1,
∴OG==﹣1,
∴OD=(﹣1)=2﹣.
25.解:四边形EFGH是正方形.
证明:∵AE=BF=CG=DH,
∴AH=DG=CF=BE.
∵∠A=∠B=∠C=∠D=90°,
∴△AEH≌△DHG≌△CGF≌△BFE,
∴EF=EH=HG=GF,∠EHA=∠HGD.
∴四边形EFGH是菱形.
∵∠EHA=∠HGD,∠HGD+∠GHD=90°,
∴∠EHA+∠GHD=90°.
∴∠EHG=90°.
∴四边形EFGH是正方形.
解答题专题训练(附答案)
1.如图,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E、F分别为边AB、AC的中点,当AD=6时,BC边上存在一点Q,使∠EQF=90°,求此时BQ的长.
2.如图,菱形ABCD的对角线相交于点O,∠BAD=60°,菱形ABCD的周长为24.
(1)求对角线BD的长;
(2)求菱形ABCD的面积.
3.如图,四边形ABCD是平行四边形,且对角线AC,BD交于点O,BD=2AB,AE∥BD,OE∥AB.求证:四边形ABOE是菱形.
4.如图,在Rt△ABC中,∠ACB=90°,CD、CE三等分∠ACB,且CD是AB边的中线,CE是BD边的中线,当DE=2时,求AC的长.
5.如图,已知在△ABC中,∠A=60°,点D是BC的中点,CE⊥AB,BF⊥AC,垂足分别为E、F,连接DE、DF、EF.
求证:△DEF为等边三角形.
6.求证:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.在探究过程中,老师发现班上的学生有两种不同辅助线添法,如图,在△ABC中,∠ACB=90°.
甲同学:以B为圆心,以BA长为半径作弧,交BC延长线于D,连接AD.
乙同学:以B为圆心,以BC长为半径作弧,交BA于D,连接CD.
请你选择上述一种做法进行证明.(要求写出已知,求证,证明过程)
7.如图,在菱形ABCD中,点E,F分别是边AB和BC上的点,且BE=BF.求证:∠DEF=∠DFE.
8.如图,在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F.
(1)求证:BE=DF.
(2)当∠BAD=110°时,求∠EAF的度数.
9.在菱形ABCD中,∠BAD=60°,点E、F分别在边AB、AD上,且AE=DF,BF与DE交于点G.
(1)如图①,连接BD.求证:△ADE≌△DBF;
(2)如图②,连接CG.求证:BG+DG=CG.
10.如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF.
(1)求证:△ABE≌△CDF;
(2)连接BD,若∠1=32°,∠ADB=22°,请直接写出当∠ABE= °时,四边形BFDE是菱形.
11.如图,在Rt△ABC,∠ABC=90°,D、E分别是边BC,AC的中点,连接ED并延长到点F,使DF=ED,连接BE、BF、CF、AD.求证:四边形BFCE是菱形.
12.如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=4,求AC的长.
13.已知:在 ABCD中,对角线AC与BD交于点O,过点O作EF⊥BD,分别交AB,DC于点E,F,连接BF,DE.
(1)如图1,求证:四边形DEBF是菱形;
(2)如图2,AD∥EF,且AD=AE,在不添加任何辅助线的条件下,请直接写出图2中四个度数为30°的角.
14.如图,点E为矩形ABCD外一点,AE=DE.求证:△ABE≌△DCE.
15.已知,在矩形ABCD中,AB=a,BC=b,动点M从点A出发沿边AD向点D运动.
当b=2a,点M运动到边AD的中点时,请证明∠BMC=90°;
16.如图,在四边形ABCD中,∠B=∠C.点E、F、G分别在边AB、BC、CD上,AE=GF=GC.
(1)求证:四边形AEFG是平行四边形;
(2)当∠FGC与∠EFB满足怎样的关系时,四边形AEFG是矩形.请说明理由.
17.如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G.
(I)求证:DF∥AC;
(2)连接DE、CF,若2AB=BF,G恰好是CD的中点,求证:四边形CFDE是矩形.
18.在平行四边形ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接DF,CF.
(1)求证:四边形DFBE是矩形;
(2)当CF平分∠DCB时,若CE=3,BC=5,求CD的长.
19.如图,在 ABCD中,点M是AD边的中点,连接BM,CM,且BM=CM.
(1)求证:四边形ABCD是矩形;
(2)若△BCM是直角三角形,直接写出AD与AB之间的数量关系.
20.(1)如图1,△ABC中,∠B=90°,AB=8,BC=6,AD=CD,求AD的长.
(2)边长分别为a和b的两个正方形按图2的样式摆放,如果阴影部分的面积为20,a+b=10,求ab的值.
21.如图,四边形ABDE和四边形ACFG都是正方形,CE与BG交于点M,点M在△ABC的外部.
(1)求证:BG=CE;(2)求证:CE⊥BG;(3)求:∠AME的度数.
22.已知:在△ABC中,CB=CA,点D、E分别是AB、AC的中点,连接DE并延长交外角∠ACM的平分线CN于点F.
(1)求证:AD=CF;
(2)连接CD,AF,当△ABC满足什么条件时,四边形ADCF为正方形?请证明你的结论.
23.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)
24.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OD的长.
25.如图,在正方形ABCD中,E,F,G,H分别在它的四条边上,且AE=BF=CG=DH.四边形EFGH是什么特殊四边形?你是如何判断的?
参考答案
1.解:∵E、F分别为边AB、AC的中点,
∴EF∥BC,EF=BC,
∵BC=12,
∴EF=6,
取EF的中点O,过点O作OQ⊥BC与Q,过点E作EG⊥BC于G,
∵AD是BC边上的高,AD=6,
∴OQ=EG=×6=3,
∴点Q即为所求的使∠EQF=90°的点,
∵EF∥BC,EG∥OQ,OE=OQ=3,
∴四边形OEQG是正方形,
∴GQ=OQ=3,
∵点E是AB的中点,
∴EG是△ABD的中位线,
∴EG=AD=3,
∵∠ABC=60°,
∴BG=EG=×3=,
∴BQ=BG+GQ=3+.
2.解:(1)∵四边形ABCD是菱形,周长为24,
∴AB=BC=CD=AD=6,AC⊥BD,OB=OD=BD,OA=OC=AC,∠BAO=∠BAD=×60°=30°,
∴∠AOB=90°,
∴OB=AB=3,
∴BD=2OB=6;
(2)由(1)得:BD=6,AB=6,OB=3,∠AOB=90°,
∴OA===3,
∴AC=2OA=6,
∴菱形ABCD的面积=AC×BD=×6×6=18.
3.证明:∵四边形ABCD是平行四边形,
∴OB=OD=BD,
∵BD=2AB,
∴AB=OB,
∵AE∥BD,OE∥AB,
∴四边形ABOE是平行四边形,
∵AB=OB,
∴四边形ABOE是菱形.
4.解:∵∠ACB=90°,CD、CE三等分∠ACB,
∴∠ACD=∠DCE=∠BCE=30°,
∵CD是AB边的中线,
∴AD=CD=BD=AB,
∴∠A=∠ACD=30°,
∵CE是BD边的中线,DE=2,
∴BD=2DE=4,
∴AB=8,
∴BC=AB=4,
∴AC==4,
故AC的长为4.
5.证明:∵CE⊥AB,BF⊥AC,
∴∠AEC=∠BEC=∠AFB=∠BFC=90°,
∵∠A=60°,
∴∠ABF=∠ACE=30°,
∴∠FBC+∠ECB=180°﹣∠A﹣∠ABF﹣∠ACE=60°,
∵点D是BC的中点,
∴DE=CD=BC,DF=BD=BC,
∴∠DEC=∠DCE,∠DBF=∠DFB,DE=DF,
∵∠BDE=∠DEC+∠DCE=2∠DCE,
∠CDF=∠DBF+∠DFB=2∠DBF,
∴∠BDE+∠CDF=2∠DBF+2∠DCE=2×60°=120°,
∴∠EDF=60°,
∴△DEF为等边三角形.
6.解:甲同学:如图1,已知在△ABC中,∠ACB=90°,∠BAC=30°,
求证:BC=AB,
证明:以B为圆心,以BA长为半径作弧,交BC延长线于D,连接AD,
则AB=BD,
∵∠ACB=90°,∠BAC=30°,
∴∠B=60°,
∴△ABD是等边三角形,
∴AD=AB,
∴BC=CD=BD=AB;
乙同学:如图2,已知在△ABC中,∠ACB=90°,∠BAC=30°,
求证:BC=AB,
证明:以B为圆心,以BC长为半径作弧,交BA于D,连接CD,
则BD=BC,
∵∠ACB=90°,∠BAC=30°,
∴∠B=60°,
∴△BCD是等边三角形,
∴CD=BD=BC,∠BDC=∠BCD=60°,
∴∠ACD=30°,
∴∠A=∠ACD,
∴AD=CD=BD=BC=AB.
7.证明:∵四边形ABCD是菱形,
∴∠A=∠C,AB=CB,AD=DC,
∵BE=BF,
∴AE=CF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴DE=DF,
∴∠DEF=∠DFE.
8.(1)证明:∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD,
∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(AAS),
∴BE=DF;
(2)解:∵四边形ABCD是菱形,
∴AD∥BC,
∴∠BAD+∠B=180°,
∵∠BAD=110°,
∴∠B=70°
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=20°,
∴∠DAF=20°,
∴∠EAF=∠BAD﹣∠BAE﹣∠DAF=110°﹣20°﹣20°=70°.
9.证明:(1)∵四边形ABCD是菱形,∠BAD=60°,
∴AB=BC=CD=AD,∠C=∠BAD=60°,
∴△ABD和△CBD都是等边三角形,
∴AD=DB,∠BDF=∠DAE=60°,
在△ADE和△DBF中,
,
∴△ADE≌△DBF(SAS);
(2)如图②,延长GB到点H,使BH=DG,连接CH、BD,
由(1)知△ADE≌△DBF,△CBD是等边三角形,
∴∠ADE=∠DBF,∠CBD=∠BCD=60°,
∴∠DBF+∠CBH=180°﹣∠CBD=120°,
∵四边形ABCD是菱形,∠BAD=60°,
∴BC=CD,∠ADC=180°﹣∠BAD=120°,
∴∠ADE+∠CDG=120°,
∴∠CBH=∠CDG,
在△CBH和△CDG中,
,
∴△CBH≌△CDG(SAS),
∴CH=CG,∠BCH=∠DCG,
∵∠BCD=∠DCG+∠BCG=60°,
∴∠BCH+∠BCG=60°,
即∠GCH=60°,
∴△CGH是等边三角形,
∴GH=CG,
∵GH=BG+BH=BG+DG,
∴BG+DG=CG.
10.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠BCD,
∴∠1=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:当∠ABE=12°时,四边形BFDE是菱形,理由如下:
∵△ABE≌△CDF,
∴BE=DF,AE=CF,
∴BF=DE,
∴四边形BFDE是平行四边形,
∵∠1=32°,∠ADB=22°,
∴∠ABD=∠1﹣∠ADB=10°,
∵∠ABE=12°,
∴∠DBE=∠ABD+∠ABE=22°,
∴∠DBE=∠ADB=22°,
∴BE=DE,
∴平行四边形BFDE是菱形,
故答案为:12.
11.证明:∵D是边BC的中点,
∴BD=CD,
∵DF=ED,
∴四边形BFCE是平行四边形,
在Rt△ABC中,∠ABC=90°,E是边AC的中点,
∴BE=CE,
∴四边形BFCE是菱形.
12.(1)证明:∵AD=2BC,E为AD的中点,
∴DE=BC,
∵AD∥BC,
∴四边形BCDE是平行四边形,
∵∠ABD=90°,AE=DE,
∴BE=DE,
∴四边形BCDE是菱形.
(2)解:连接AC.
∵AD∥BC,AC平分∠BAD,
∴∠BAC=∠DAC=∠BCA,
∴AB=BC=4,
∵AD=2BC=8,
∴sin∠ADB=,
∴∠ADB=30°,
∴∠DAC=30°,∠ADC=60°,
∴∠ACD=90°,
在Rt△ACD中,∵AD=8,
∴CD=4,AC=4.
13.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠OBE=∠ODF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA),
∴BE=DF,
∵BE∥DF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形;
(2)解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AD∥EF,
∴四边形ADFE是平行四边形,
∴AE=DF,
由(1)得:四边形DEBF是菱形,
∴DE=DF=BE,
∴AD=DE,
∵AD=AE,
∴AD=AE=DE,
∴△ADE是等边三角形,
∴∠AED=60°,
∵DE=BE,
∴∠EDB=∠EBD=∠AED=30°,
同理:∠FDB=∠FBD=30°,
即图2中四个度数为30°的角为∠EDB、∠EBD、∠FDB、∠FBD.
14.证明:∵AE=DE.
∴∠EAD=∠EDA,
∵四边形ABCD是矩形,
∴AB=CD,∠BAD=∠CDA,
∴∠EAD+∠BAD=∠EDA+∠CDA,
∴∠EAB=∠EDC,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS).
15.(1)证明:∵b=2a,点M是AD的中点,
∴AB=AM=MD=DC=a,
在矩形ABCD中,∠A=∠D=90°,
∴∠AMB=∠DMC=45°,
∴∠BMC=90°.
16.(1)证明:在四边形ABCD中,∠B=∠C,
∵GF=GC,
∴∠C=∠GFC,∠B=∠GFC,
∴AB∥GF,
即AE∥GF,
∵AE=GF,
∴四边形AEFG是平行四边形.
(2)解:当∠FGC=2∠EFB时,四边形AEFG是矩形,
理由:∵∠FGC+∠GFC+∠C=180o,∠GFC=∠C,∠FGC=2∠EFB,
∴2∠GFC+2∠EFB=180°,
∴∠BFE+∠GFC=90°.
∴∠EFG=90°.
∵四边形AEFG是平行四边形,
∴四边形AEFG是矩形.
17.(1)证明:连接BD,交AC于点O,如图所示:
∵四边形ABCD是平行四边形,
∴BO=DO,
∵BE=EF,
∴OE是△BDF的中位线,
∴OE∥DF,
即DF∥AC;
(2)证明:如图所示:
由(1)得:DF∥AC,
∴∠DFG=∠CEG,∠GDF=∠GCE,
∵G是CD的中点,
∴DG=CG,
在△DFG和△CEG中,
,
∴△DFG≌△CEG(AAS),
∴FG=EG,
∴四边形CFDE是平行四边形,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵2AB=BF,
∴2CD=BF,
又∵EF=BE,
∴CD=EF,
∴平行四边形CFDE是矩形.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED.
∴四边形DFBE是平行四边形,
∵BE⊥CD,
∴∠BED=90°.
∴四边形DFBE是矩形;
(2)解:由(1)得:四边形DFBE是矩形,
∴DE=BF,
∵CF平分∠DCB,
∴∠DCF=∠BCF,
∵AB∥CD,
∴∠DCF=∠CFB,
∴∠BCF=∠CFB,
∴BF=BC=5,
∴DE=BF=5,
∴CD=DE+CE=5+3=8.
19.(1)证明:∵点M是AD边的中点,
∴AM=DM,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥CD,
在△ABM和△DCM中,
,
∴△ABM≌△DCM(SSS),
∴∠A=∠D,
∵AB∥CD,
∴∠A+∠D=180°,
∴∠A=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
(2)解:AD与AB之间的数量关系:AD=2AB,理由如下:
∵△BCM是直角三角形,BM=CM,
∴△BCM是等腰直角三角形,
∴∠MBC=45°,
由(1)得:四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠AMB=∠MBC=45°,
∴△ABM是等腰直角三角形,
∴AB=AM,
∵点M是AD边的中点,
∴AD=2AM
∴AD=2AB.
20.解:(1)设AD=CD=x,则BD=8﹣x,
∵∠B=90°,BD=8﹣x,BC=6,CD=x,
∴(8﹣x)2+62=x2,
解得x=,
即AD的长为;
(2)由图可得,
b2﹣a(b﹣a)=20,
化简,得:a2﹣ab+b2=40①,
∵a+b=10,
∴(a+b)2=100,
∴a2+2ab+b2=100②,
②﹣①,得
3ab=60,
解得ab=20.
21.(1)证明:在正方形ABDE和ACFG中,AB=AE,AC=AG,∠BAE=∠CAG=90°,
∴∠BAE+∠BAC=∠CAG+∠BAC,
即∠CAE=∠BAG,
∵在△ABG和△AEC中,
,
∴△ABG≌△AEC(SAS),
∴BG=CE;
(2)证明:设BG、CE相交于点N,
∵△ABG≌△AEC,
∴∠ACE=∠AGB,
∵∠NCF+∠NGF=∠ACF+∠AGF=90°+90°=180°,
∴∠CNG=360°﹣(∠NCF+∠NGF+∠F)=360°﹣(180°+90°)=90°,
∴BG⊥CE;
(3)解:过A作BG,CE的垂线段交于点P,Q,
∵△ABG≌△AEC,
∴AP=AQ,
∴AM是角平分线,
∴∠AMC=45°,
∴∠AME=135°.
22.(1)证明:∵CB=CA,
∴∠A=∠B,
∵∠ACM=∠A+∠B,
∴∠A=ACM,
∵CN平分∠ACM,
∴∠ACF=ACM,
∴∠A=∠ACF,
∵E是AC的中点,
∴AE=CE,
在△ADE与△CFE中,
,
∴△ADE≌△CFE(ASA),
∴AD=CF;
(2)解:当△ABC满足∠ACB=90°,四边形ADCF是正方形,
证明:连接CD,AF,
∵AC=BC,∠ACB=90°,
∴△ACB是等腰直角三角形,
∴∠BAC=45°,
∵CN平分∠ACM,
∴∠ACF=ACM=45°,
∴∠DAC=∠ACF,
∴AD∥CF,
由(1)知AD=CF,
∴四边形ADCF是平行四边形,
∵点D是AB的中点,
∴AD=CD,
∴∠ACD=∠CAD=45°,
∴∠DCF=90°,
∴矩形ADCF是正方形.
23.(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
(3)解:当∠A=45°时,四边形BECD是正方形,
理由:∵∠ACB=90°,
∴∠ABC=45°,
由(2)可知,四边形BECD是菱形,
∴∠ABC=∠CBE=45°,
∴∠DBE=90°,
∴四边形BECD是正方形.
24.(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)∵四边形ABEF是正方形,
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∵AD=AE,
∴AD﹣AF=AE﹣AG,
即DF=EG,
在△DFO和△EGO中,,
∴△DFO≌△EGO(AAS),
∴FO=GO,FD=EG
∵∠DAE=∠AEF=45°,∠AFE=∠AGD=90°,
∴DF=FO=OG=EG,
∴DO=OF=OG,
∴DG=DO+OG=OG+OG=1,
∴OG==﹣1,
∴OD=(﹣1)=2﹣.
25.解:四边形EFGH是正方形.
证明:∵AE=BF=CG=DH,
∴AH=DG=CF=BE.
∵∠A=∠B=∠C=∠D=90°,
∴△AEH≌△DHG≌△CGF≌△BFE,
∴EF=EH=HG=GF,∠EHA=∠HGD.
∴四边形EFGH是菱形.
∵∠EHA=∠HGD,∠HGD+∠GHD=90°,
∴∠EHA+∠GHD=90°.
∴∠EHG=90°.
∴四边形EFGH是正方形.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
