2021-2022学年华师大版八年级数学下册18.1平行四边形的性质同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年华师大版八年级数学下册18.1平行四边形的性质同步练习题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 159.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 12:13:05 | ||
图片预览



文档简介
2021-2022学年华师大版八年级数学下册《18-1平行四边形的性质》同步练习题(附答案)
一.选择题
1.如图,将 ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
A.66° B.104° C.114° D.124°
2.如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
3.如图 ABCD中,AD=6,AB=4,DE平分∠ADC交BC于点E,则BE的长是( )
A.2 B.3 C.4 D.5
4.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
A.8 B.10 C.12 D.14
5.如图, ABCD中,对角线AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,若 ABCD的周长为28,则△ABE的周长为( )
A.28 B.24 C.21 D.14
二.填空题
6.如图,在 ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 .
7.在 ABCD中,AD=BD,BE是AD边上的高,∠EBD=20°,则∠A的度数为 .
8.如图,在 ABCD中,E、F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为 .
9.如图, ABCD的顶点C在等边△BEF的边BF上,点E在AB的延长线上,G为DE的中点,连接CG.若AD=3,AB=CF=2,则CG的长为 .
10.如图,在 ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为 .
三.解答题
11.如图, ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
12.如图,在平行四边形ABCD中,对角线AC和BD相交于点O,BD⊥AD,AB=10,AD=8,求OB的长度及平行四边形ABCD的面积.
13.如图,四边形ABCD是平行四边形,E,F是对角线AC的三等分点,连接BE,DF.证明:BE=DF.
14.在 ABCD中,E是DC的中点,连接AE并延长,交BC的延长线于点F.
(1)求证:BC=CF;
(2)点G是CF上一点,连接AG交CD于点H,且∠DAF=∠GAF.若CG=2,GF=5,求AH的长.
15.如图,在平行四边形ABCD中,点F是AD中点,连接CF并延长交BA的延长线于点E.
(1)求证:AB=AE.
(2)若BC=2AE,∠E=31°,求∠DAB的度数.
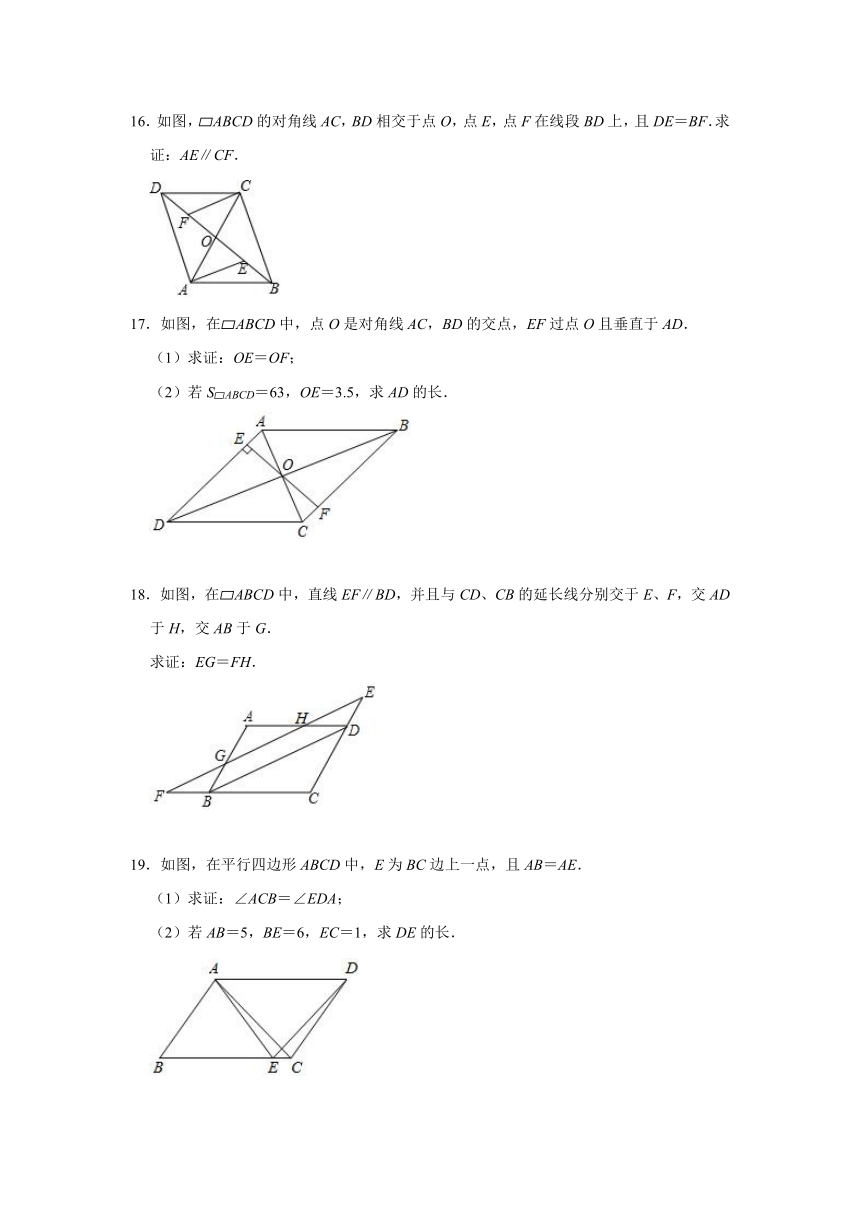
16.如图, ABCD的对角线AC,BD相交于点O,点E,点F在线段BD上,且DE=BF.求证:AE∥CF.
17.如图,在 ABCD中,点O是对角线AC,BD的交点,EF过点O且垂直于AD.
(1)求证:OE=OF;
(2)若S ABCD=63,OE=3.5,求AD的长.
18.如图,在 ABCD中,直线EF∥BD,并且与CD、CB的延长线分别交于E、F,交AD于H,交AB于G.
求证:EG=FH.
19.如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:∠ACB=∠EDA;
(2)若AB=5,BE=6,EC=1,求DE的长.
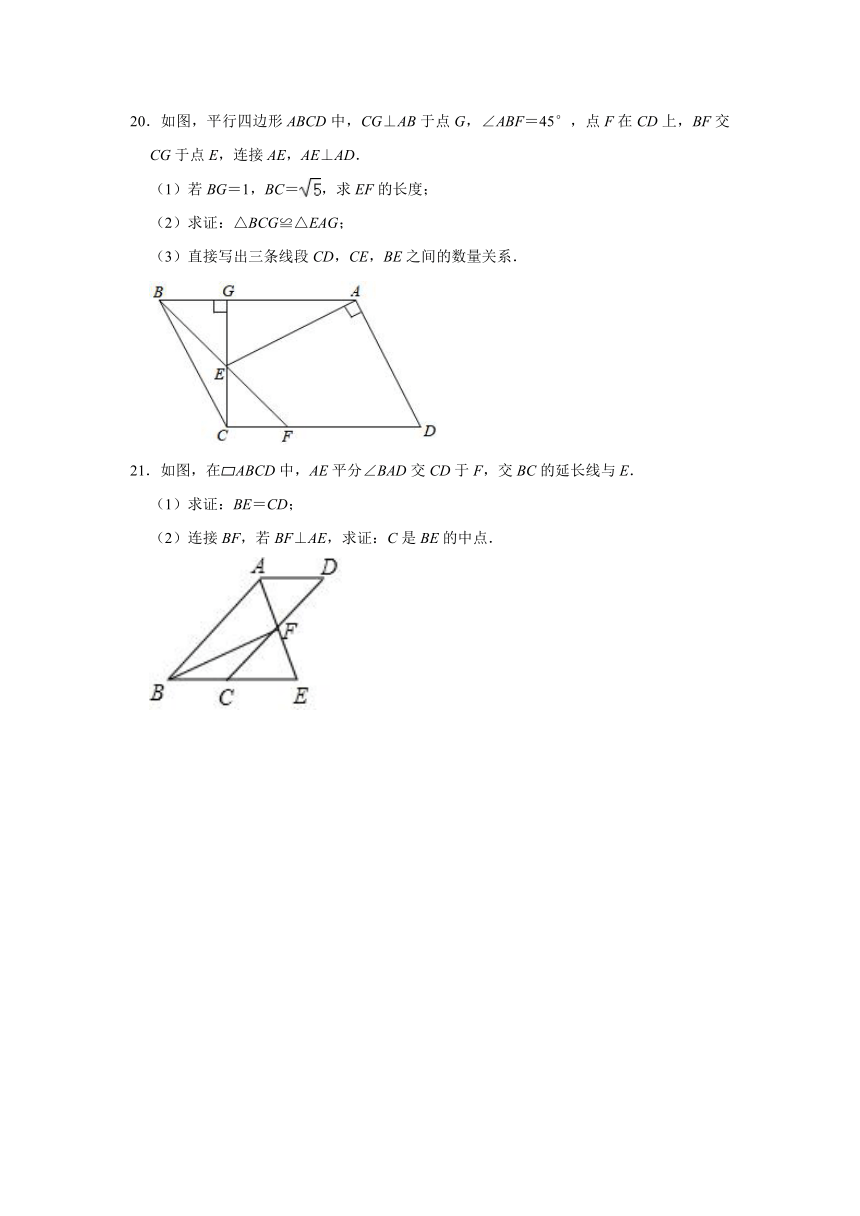
20.如图,平行四边形ABCD中,CG⊥AB于点G,∠ABF=45°,点F在CD上,BF交CG于点E,连接AE,AE⊥AD.
(1)若BG=1,BC=,求EF的长度;
(2)求证:△BCG≌△EAG;
(3)直接写出三条线段CD,CE,BE之间的数量关系.
21.如图,在 ABCD中,AE平分∠BAD交CD于F,交BC的延长线与E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,求证:C是BE的中点.
参考答案
一.选择题
1.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=∠1=22°,
∴∠B=180°﹣∠2﹣∠BAC=180°﹣44°﹣22°=114°;
故选:C.
2.解:∵ ABCD的对角线AC与BD相交于点O,
∴BO=DO,AO=CO,
∵AB⊥AC,AB=4,AC=6,
∴∠BAO=90°,OA=3
∴BO==5,
∴BD=2BO=10,
故选:C.
3.解:∵四边形ABCD是平行四边形,
∴BC=AD=6,CD=AB=4,AD∥BC,
∴∠ADE=∠DEC,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠CDE=∠DEC,
∴EC=CD=4,
∴BE=BC﹣EC=2.
故选:A.
4.解:∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
则∠ABF=∠AFB,
∴AF=AB=6,
同理可证:DE=DC=6,
∵EF=AF+DE﹣AD=2,
即6+6﹣AD=2,
解得:AD=10;
故选:B.
5.解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC,
∵ ABCD的周长为28,
∴AB+AD=14
∵OE⊥BD,
∴OE是线段BD的中垂线,
∴BE=ED,
∴△ABE的周长=AB+BE+AE=AB+AD=14,
故选:D.
二.填空题
6.解:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°﹣∠EAD′﹣∠D′=108°,
∴∠FED′=108°﹣72°=36°;
故答案为:36°.
7.解:情形一:当E点在线段AD上时,如图所示,
∵BE是AD边上的高,∠EBD=20°,
∴∠ADB=90°﹣20°=70°,
∵AD=BD,
∴∠A=∠ABD==55°.
情形二:当E点在AD的延长线上时,如图所示,
∵BE是AD边上的高,∠EBD=20°,
∴∠BDE=70°,
∵AD=BD,
∴∠A=∠ABD=∠BDE=×70°=35°.
故答案为:55°或35°.
8.解:设∠ADE=x,
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,
∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,
解得:x=21°,
即∠ADE=21°;
故答案为:21°.
9.解:∵四边形ABCD是平行四边形,
∴AD=BC,CD=AB,DC∥AB,
∵AD=3,AB=CF=2,
∴CD=2,BC=3,
∴BF=BC+CF=5,
∵△BEF是等边三角形,G为DE的中点,
∴BF=BE=5,DG=EG,
延长CG交BE于点H,
∵DC∥AB,
∴∠CDG=∠HEG,
在△DCG和△EHG中,
,
∴△DCG≌△EHG(ASA),
∴DC=EH,CG=HG,
∵CD=2,BE=5,
∴HE=2,BH=3,
∵∠CBH=60°,BC=BH=3,
∴△CBH是等边三角形,
∴CH=BC=3,
∴CG=CH=,
故答案为:.
10.解:根据作图的方法得:BE平分∠ABC,
∴∠ABE=∠CBE
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=3,
∴DE=AD﹣AE=5﹣3=2;
故答案为:2.
三.解答题
11.(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB,
∴∠ODF=∠OBE,
在△ODF与△OBE中
∴△ODF≌△OBE(AAS)
∴BO=DO;
(2)解:∵BD⊥AD,
∴∠ADB=90°,
∵∠A=45°,
∴∠DBA=∠A=45°,
∵EF⊥AB,
∴∠G=∠A=45°,
∴△ODG是等腰直角三角形,
∵AB∥CD,EF⊥AB,
∴DF⊥OG,
∴OF=FG,△DFG是等腰直角三角形,
∵△ODF≌△OBE(AAS)
∴OE=OF,
∴GF=OF=OE,
即2FG=EF,
∵△DFG是等腰直角三角形,
∴DF=FG=1,∴DG==DO,
∴在等腰Rt△ADB 中,DB=2DO=2=AD
∴AD=2,
12.解:在平行四边形ABCD中,BC=AD=8,AD∥BC,AD=8,
∵BD⊥AD,AB=10,
∴BD==6.
∵四边形ABCD是平行四边形,
∴OB=BD=3,S ABCD=AD BD=8×6=48.
13.证明:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∴∠BAC=∠DCA,
∵E,F是对角线AC的三等分点,
∴AE=CF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
14.证明:(1)∵四边形ABC为平行四边形,
∴AD∥BC,AD=BC,
∴∠DAE=∠F,∠D=∠ECF,
∵E是DC的中点,
∴CE=DE,
在△AED和△FEC中,
,
∴△AED≌△FEC(AAS),
∴AD=FC,
∴BC=CF;
(2)∵AD∥BC,
∴∠DAF=∠F,
∵∠GAF=∠DAF,
∴∠GAF=∠F,
∴AG=GF=5,
∵CG=2,
∴AD=CF=7,
∵AD∥BC,
∴∠D=∠DCF,∠AHD=∠GHC,
∴AH=.
15.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,BC=AD,
∴∠E=∠DCF,
∵点F是AD中点,
∴AF=DF,
∵∠EFA=∠CFD,
∴△AFE≌△DFC(AAS),
∴CD=AE,
∴AB=AE;
(2)解:由(1)可得AF=DF,BC=AD,
∵BC=2AE,
∴AE=AF,
∵∠E=31°,
∴∠AFE=∠E=31°,
∴∠DAB=2∠E=62°.
16.证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS),
∴∠AED=∠CFB,
∴AE∥CF.
17.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
∵∠EAO=∠FCO,OA=OC,∠AOE=∠COF,
∴△AEO≌△CFO,(ASA)
∴OE=OF;
(2)∵OE=OF,OE=3.5,
∴EF=2OE=7,
又∵EF⊥AD,
∴S ABCD=AD×EF=63,
∴AD=9.
18.证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵EF∥BD,
∴四边形FBDH为平行四边形.
∴FH=BD.
∵EF∥BD,AB∥DC,
∴四边形BDEG是平行四边形.
∴BD=EG.
∴EG=FH.
19.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠AEB=∠EAD,
∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠EAD,
在△ABC和△EAD中,
,
∴△ABC≌△EAD(SAS),
∴∠ACB=∠EDA;
(2)如图,过点A作AF⊥BC于点F,
∵AB=AE,AB=5,BE=6,EC=1,
∴BF=EF=BE=3,FC=FE+EC=4,
在Rt△ABF和Rt△AFC中,
由勾股定理得,,
由(1)得△ABC≌△EAD,
∴.
20.解:(1)∵CG⊥AB,
∴∠AGC=∠BGC=90°,
∵BG=1,BC=,
∴,
∵∠ABF=45°,
∴BG=EG=1,
∴EC=1,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠GCD=∠BGC=90°,∠EFC=∠GBE=45°,
∴CF=CE=1,
∴;
(2)如图,延长AE交BC于H,
∵四边形ABCD是平行四边形,
∴BC∥AD,AB=CD,
∵AE⊥AD,
∴∠AHB=∠HAD=90°,
∴∠BAH+∠ABH=∠BCG+∠CBG=90°,
∴∠GAE=∠GCB,
在△BCG与△EAG中,
,
∴△BCG≌△EAG(AAS),
(3)CD﹣CE=BE,
∵△BCG≌△EAG,
∴BG=GE,CG=AG,
∵∠BGC=90°,
∴BE=BG=GE,
(2)CE+BE=CD,
∵△BCG≌△EAG(AAS),
∴AG=CG,
∴AB=BG+AG=CE+EG+BG,
∵BG=EG=BE,
∴CE+BE=AB=CD.
21.证明:(1)∵四边形ABCD为平行四边形,
∴AB=CD,AD∥BE,
∴∠DAE=∠E,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠E,
∴AB=BE,
∴BE=CD;
(2)∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠E=∠DAE,
∴∠E=∠BAE,
∴AB=BE,
∴△ABE是等腰三角形,
∵BF⊥AE,
∴AF=FE,
在△ADF与△ECF中,
,
∴△ADF≌△ECF(AAS),
∴AD=CE,
∵AD=BC,
∴BC=CE,
∴C是BE的中点.
一.选择题
1.如图,将 ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
A.66° B.104° C.114° D.124°
2.如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
3.如图 ABCD中,AD=6,AB=4,DE平分∠ADC交BC于点E,则BE的长是( )
A.2 B.3 C.4 D.5
4.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
A.8 B.10 C.12 D.14
5.如图, ABCD中,对角线AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,若 ABCD的周长为28,则△ABE的周长为( )
A.28 B.24 C.21 D.14
二.填空题
6.如图,在 ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 .
7.在 ABCD中,AD=BD,BE是AD边上的高,∠EBD=20°,则∠A的度数为 .
8.如图,在 ABCD中,E、F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为 .
9.如图, ABCD的顶点C在等边△BEF的边BF上,点E在AB的延长线上,G为DE的中点,连接CG.若AD=3,AB=CF=2,则CG的长为 .
10.如图,在 ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为 .
三.解答题
11.如图, ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
12.如图,在平行四边形ABCD中,对角线AC和BD相交于点O,BD⊥AD,AB=10,AD=8,求OB的长度及平行四边形ABCD的面积.
13.如图,四边形ABCD是平行四边形,E,F是对角线AC的三等分点,连接BE,DF.证明:BE=DF.
14.在 ABCD中,E是DC的中点,连接AE并延长,交BC的延长线于点F.
(1)求证:BC=CF;
(2)点G是CF上一点,连接AG交CD于点H,且∠DAF=∠GAF.若CG=2,GF=5,求AH的长.
15.如图,在平行四边形ABCD中,点F是AD中点,连接CF并延长交BA的延长线于点E.
(1)求证:AB=AE.
(2)若BC=2AE,∠E=31°,求∠DAB的度数.
16.如图, ABCD的对角线AC,BD相交于点O,点E,点F在线段BD上,且DE=BF.求证:AE∥CF.
17.如图,在 ABCD中,点O是对角线AC,BD的交点,EF过点O且垂直于AD.
(1)求证:OE=OF;
(2)若S ABCD=63,OE=3.5,求AD的长.
18.如图,在 ABCD中,直线EF∥BD,并且与CD、CB的延长线分别交于E、F,交AD于H,交AB于G.
求证:EG=FH.
19.如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:∠ACB=∠EDA;
(2)若AB=5,BE=6,EC=1,求DE的长.
20.如图,平行四边形ABCD中,CG⊥AB于点G,∠ABF=45°,点F在CD上,BF交CG于点E,连接AE,AE⊥AD.
(1)若BG=1,BC=,求EF的长度;
(2)求证:△BCG≌△EAG;
(3)直接写出三条线段CD,CE,BE之间的数量关系.
21.如图,在 ABCD中,AE平分∠BAD交CD于F,交BC的延长线与E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,求证:C是BE的中点.
参考答案
一.选择题
1.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=∠1=22°,
∴∠B=180°﹣∠2﹣∠BAC=180°﹣44°﹣22°=114°;
故选:C.
2.解:∵ ABCD的对角线AC与BD相交于点O,
∴BO=DO,AO=CO,
∵AB⊥AC,AB=4,AC=6,
∴∠BAO=90°,OA=3
∴BO==5,
∴BD=2BO=10,
故选:C.
3.解:∵四边形ABCD是平行四边形,
∴BC=AD=6,CD=AB=4,AD∥BC,
∴∠ADE=∠DEC,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠CDE=∠DEC,
∴EC=CD=4,
∴BE=BC﹣EC=2.
故选:A.
4.解:∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
则∠ABF=∠AFB,
∴AF=AB=6,
同理可证:DE=DC=6,
∵EF=AF+DE﹣AD=2,
即6+6﹣AD=2,
解得:AD=10;
故选:B.
5.解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC,
∵ ABCD的周长为28,
∴AB+AD=14
∵OE⊥BD,
∴OE是线段BD的中垂线,
∴BE=ED,
∴△ABE的周长=AB+BE+AE=AB+AD=14,
故选:D.
二.填空题
6.解:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°﹣∠EAD′﹣∠D′=108°,
∴∠FED′=108°﹣72°=36°;
故答案为:36°.
7.解:情形一:当E点在线段AD上时,如图所示,
∵BE是AD边上的高,∠EBD=20°,
∴∠ADB=90°﹣20°=70°,
∵AD=BD,
∴∠A=∠ABD==55°.
情形二:当E点在AD的延长线上时,如图所示,
∵BE是AD边上的高,∠EBD=20°,
∴∠BDE=70°,
∵AD=BD,
∴∠A=∠ABD=∠BDE=×70°=35°.
故答案为:55°或35°.
8.解:设∠ADE=x,
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,
∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,
解得:x=21°,
即∠ADE=21°;
故答案为:21°.
9.解:∵四边形ABCD是平行四边形,
∴AD=BC,CD=AB,DC∥AB,
∵AD=3,AB=CF=2,
∴CD=2,BC=3,
∴BF=BC+CF=5,
∵△BEF是等边三角形,G为DE的中点,
∴BF=BE=5,DG=EG,
延长CG交BE于点H,
∵DC∥AB,
∴∠CDG=∠HEG,
在△DCG和△EHG中,
,
∴△DCG≌△EHG(ASA),
∴DC=EH,CG=HG,
∵CD=2,BE=5,
∴HE=2,BH=3,
∵∠CBH=60°,BC=BH=3,
∴△CBH是等边三角形,
∴CH=BC=3,
∴CG=CH=,
故答案为:.
10.解:根据作图的方法得:BE平分∠ABC,
∴∠ABE=∠CBE
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=3,
∴DE=AD﹣AE=5﹣3=2;
故答案为:2.
三.解答题
11.(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB,
∴∠ODF=∠OBE,
在△ODF与△OBE中
∴△ODF≌△OBE(AAS)
∴BO=DO;
(2)解:∵BD⊥AD,
∴∠ADB=90°,
∵∠A=45°,
∴∠DBA=∠A=45°,
∵EF⊥AB,
∴∠G=∠A=45°,
∴△ODG是等腰直角三角形,
∵AB∥CD,EF⊥AB,
∴DF⊥OG,
∴OF=FG,△DFG是等腰直角三角形,
∵△ODF≌△OBE(AAS)
∴OE=OF,
∴GF=OF=OE,
即2FG=EF,
∵△DFG是等腰直角三角形,
∴DF=FG=1,∴DG==DO,
∴在等腰Rt△ADB 中,DB=2DO=2=AD
∴AD=2,
12.解:在平行四边形ABCD中,BC=AD=8,AD∥BC,AD=8,
∵BD⊥AD,AB=10,
∴BD==6.
∵四边形ABCD是平行四边形,
∴OB=BD=3,S ABCD=AD BD=8×6=48.
13.证明:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∴∠BAC=∠DCA,
∵E,F是对角线AC的三等分点,
∴AE=CF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
14.证明:(1)∵四边形ABC为平行四边形,
∴AD∥BC,AD=BC,
∴∠DAE=∠F,∠D=∠ECF,
∵E是DC的中点,
∴CE=DE,
在△AED和△FEC中,
,
∴△AED≌△FEC(AAS),
∴AD=FC,
∴BC=CF;
(2)∵AD∥BC,
∴∠DAF=∠F,
∵∠GAF=∠DAF,
∴∠GAF=∠F,
∴AG=GF=5,
∵CG=2,
∴AD=CF=7,
∵AD∥BC,
∴∠D=∠DCF,∠AHD=∠GHC,
∴AH=.
15.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,BC=AD,
∴∠E=∠DCF,
∵点F是AD中点,
∴AF=DF,
∵∠EFA=∠CFD,
∴△AFE≌△DFC(AAS),
∴CD=AE,
∴AB=AE;
(2)解:由(1)可得AF=DF,BC=AD,
∵BC=2AE,
∴AE=AF,
∵∠E=31°,
∴∠AFE=∠E=31°,
∴∠DAB=2∠E=62°.
16.证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS),
∴∠AED=∠CFB,
∴AE∥CF.
17.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
∵∠EAO=∠FCO,OA=OC,∠AOE=∠COF,
∴△AEO≌△CFO,(ASA)
∴OE=OF;
(2)∵OE=OF,OE=3.5,
∴EF=2OE=7,
又∵EF⊥AD,
∴S ABCD=AD×EF=63,
∴AD=9.
18.证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵EF∥BD,
∴四边形FBDH为平行四边形.
∴FH=BD.
∵EF∥BD,AB∥DC,
∴四边形BDEG是平行四边形.
∴BD=EG.
∴EG=FH.
19.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠AEB=∠EAD,
∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠EAD,
在△ABC和△EAD中,
,
∴△ABC≌△EAD(SAS),
∴∠ACB=∠EDA;
(2)如图,过点A作AF⊥BC于点F,
∵AB=AE,AB=5,BE=6,EC=1,
∴BF=EF=BE=3,FC=FE+EC=4,
在Rt△ABF和Rt△AFC中,
由勾股定理得,,
由(1)得△ABC≌△EAD,
∴.
20.解:(1)∵CG⊥AB,
∴∠AGC=∠BGC=90°,
∵BG=1,BC=,
∴,
∵∠ABF=45°,
∴BG=EG=1,
∴EC=1,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠GCD=∠BGC=90°,∠EFC=∠GBE=45°,
∴CF=CE=1,
∴;
(2)如图,延长AE交BC于H,
∵四边形ABCD是平行四边形,
∴BC∥AD,AB=CD,
∵AE⊥AD,
∴∠AHB=∠HAD=90°,
∴∠BAH+∠ABH=∠BCG+∠CBG=90°,
∴∠GAE=∠GCB,
在△BCG与△EAG中,
,
∴△BCG≌△EAG(AAS),
(3)CD﹣CE=BE,
∵△BCG≌△EAG,
∴BG=GE,CG=AG,
∵∠BGC=90°,
∴BE=BG=GE,
(2)CE+BE=CD,
∵△BCG≌△EAG(AAS),
∴AG=CG,
∴AB=BG+AG=CE+EG+BG,
∵BG=EG=BE,
∴CE+BE=AB=CD.
21.证明:(1)∵四边形ABCD为平行四边形,
∴AB=CD,AD∥BE,
∴∠DAE=∠E,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠E,
∴AB=BE,
∴BE=CD;
(2)∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠E=∠DAE,
∴∠E=∠BAE,
∴AB=BE,
∴△ABE是等腰三角形,
∵BF⊥AE,
∴AF=FE,
在△ADF与△ECF中,
,
∴△ADF≌△ECF(AAS),
∴AD=CE,
∵AD=BC,
∴BC=CE,
∴C是BE的中点.
