2021-2022学年鲁教版(五四制)七年级数学下册8.5平行线的性质定理填空题优生辅导训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学下册8.5平行线的性质定理填空题优生辅导训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 178.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 12:13:08 | ||
图片预览


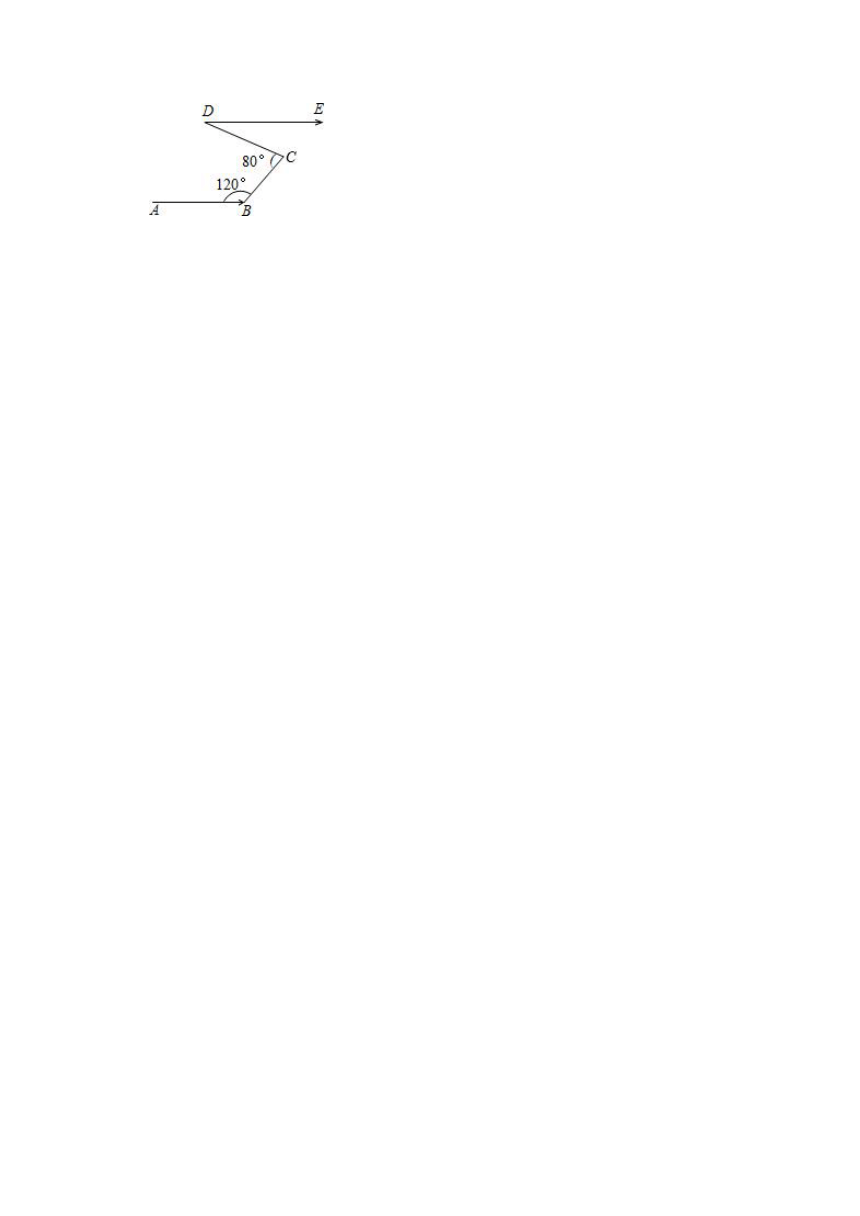
文档简介
2021-2022学年鲁教版七年级数学下册《8.5平行线的性质定理》
填空题优生辅导训练(附答案)
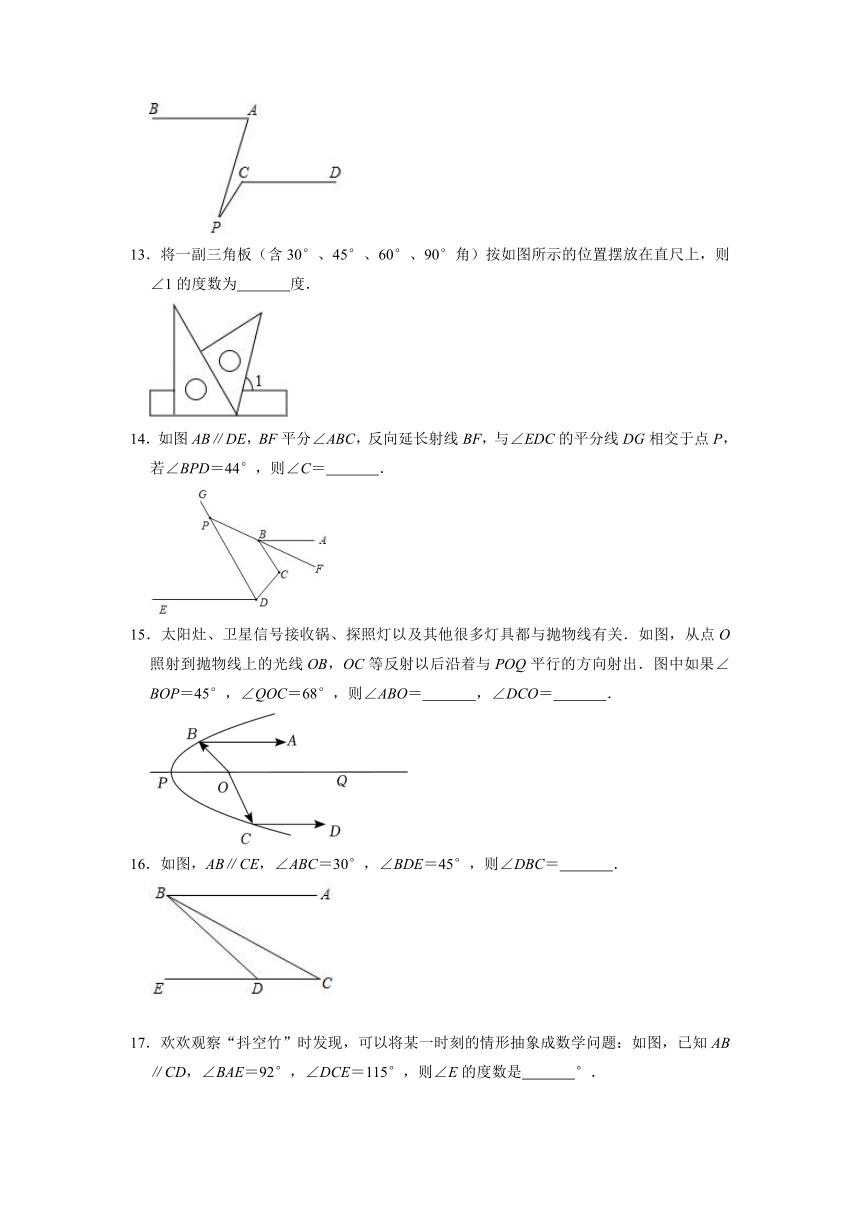
1.将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2= .
2.武侯祠博物馆享有“三国圣地”的美誉,它的大门的栏杆示意图如图所示,BA⊥AE于点A,CD∥AE,若∠BCD=120°,那么∠ABC= 度.
3.如图,AB∥CD,EF⊥BD,垂足为F,∠1=43°,则∠2的度数为 .
4.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的度数为 .
5.如图CD⊥AB于D,EF⊥AB于F,∠DGC=105°,∠BCG=75°,则∠1+∠2= .
6.如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠D=50°,则下列结论:①∠AOE=65°;②OF平分∠BOD;③∠GOE=∠DOF;④∠GOE=25°.其中正确说法的序号是 .
7.若∠A和∠B的两边分别平行,且∠A比∠B的两倍少30°,则∠B的度数是 .
8.已知,如图,AB∥CD,则∠α、∠β、∠γ之间的关系为 .
9.如图所示,AB∥CD,则∠A+∠E+∠F+∠C= .
10.如图①:MA1∥NA2,图②:MA1∥NA3,图③:MA1∥NA4,图④:MA1∥NA5,……,
则第7个图中的∠A1+∠A2+∠A3+…+∠A8= .
11.如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.
(1)∠1、∠2、∠3之间的关系为 ;
(2)如果点P在A、B两点之间运动时,∠1、∠2、∠3之间的关系为 ;
(3)如果点P(点P和A、B不重合)在A、B两点外侧运动时,∠1、∠2、∠3之间关系为 .
12.如图,已知AB∥CD,则∠A、∠C、∠P的关系为 .
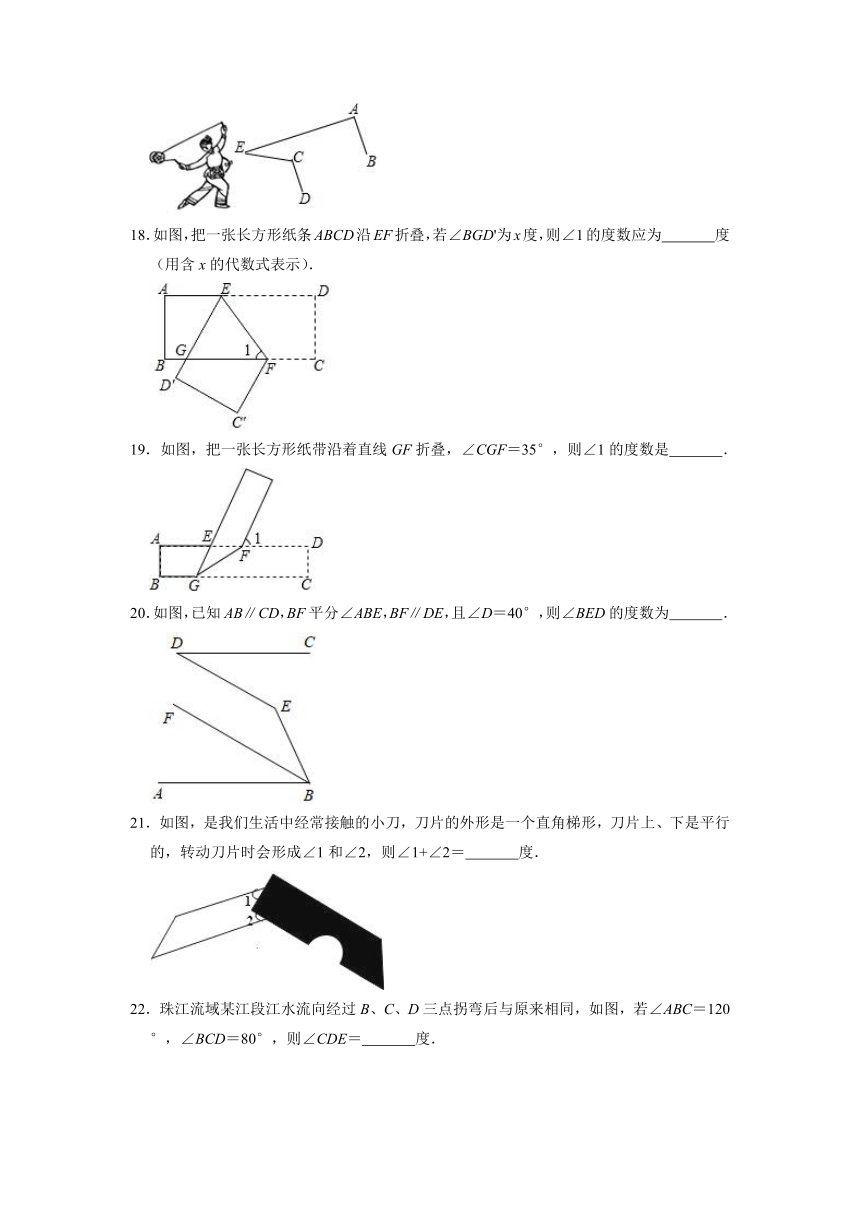
13.将一副三角板(含30°、45°、60°、90°角)按如图所示的位置摆放在直尺上,则∠1的度数为 度.
14.如图AB∥DE,BF平分∠ABC,反向延长射线BF,与∠EDC的平分线DG相交于点P,若∠BPD=44°,则∠C= .
15.太阳灶、卫星信号接收锅、探照灯以及其他很多灯具都与抛物线有关.如图,从点O照射到抛物线上的光线OB,OC等反射以后沿着与POQ平行的方向射出.图中如果∠BOP=45°,∠QOC=68°,则∠ABO= ,∠DCO= .
16.如图,AB∥CE,∠ABC=30°,∠BDE=45°,则∠DBC= .
17.欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是 °.
18.如图,把一张长方形纸条ABCD沿EF折叠,若∠BGD'为x度,则∠1的度数应为 度(用含x的代数式表示).
19.如图,把一张长方形纸带沿着直线GF折叠,∠CGF=35°,则∠1的度数是 .
20.如图,已知AB∥CD,BF平分∠ABE,BF∥DE,且∠D=40°,则∠BED的度数为 .
21.如图,是我们生活中经常接触的小刀,刀片的外形是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2= 度.
22.珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE= 度.
参考答案
1.证明:如图,过点B作BN∥FG,
∵四边形EFGH是矩形纸片,
∴EH∥FG,
∴BN∥EH∥FG,
∴∠1=∠3,∠2=∠4,
∴∠1+∠2=∠3+∠4=∠ABC=90°,
即∠1+∠2=90°.
故答案为:90°.
2.解:过点B作BN∥AE,如图所示:
∵CD∥AE,
∴BN∥CD,
∴∠BCD+∠CBN=180°,
∴∠CBN=180°﹣∠BCD=180°﹣120°=60°,
∵BA⊥AE,
∴BN⊥BA,
∴∠ABN=90°,
∴∠ABC=∠CBN+∠ABN=60°+90°=150°,
故答案为:150.
3.解:∵AB∥CD,
∴∠D=∠1=43°.
∵EF⊥BD,垂足为F,
∴∠DFE=90°,
∴∠2=180°﹣90°﹣43°=47°.
故答案为:47°.
4.解:过点B作BD∥l,
∵直线l∥m,
∴BD∥l∥m,
∴∠4=∠1,∠2=∠3,
∴∠1+∠2=∠3+∠4=∠ABC,
∵∠ABC=45°,
∴∠1+∠2=45°.
故答案为:45°.
5.解:∵∠DGC=105°,∠BCG=75°(已知),
∴∠DGC+∠BCG=180°,
∴DG∥BC(同旁内角互补,两直线平行),
∴∠1=∠DCB(两直线平行,内错角相等),
∵CD⊥AB,EF⊥AB(已知),
∴CD∥EF(平面内,垂直于同一直线的两直线平行),
∴∠DCB+∠2=180°(两直线平行,同旁内角互补),
∴∠1+∠2=180°(等量代换),
故答案为:180°.
6.解:∵AB∥CD,
∴∠BOD=∠CDO=50°,
∴∠AOD=180°﹣50°=130°,
又∵OE平分∠AOD,
∴∠AOE=∠AOD=65°,
故①正确;
∵OG⊥CD,
∴∠GOA=∠DGO=90°,
∴∠GOD=40°,∠GOE=90°﹣∠AOE=25°,
∴∠EOG+∠GOD=65°,
又OE⊥OF,
∴∠DOF=25°,
∴∠BOF=∠DOF=25°,
∴OF平分∠BOD,∠GOE=∠DOF,故②③④正确;
故答案是:①②③④.
7.解:∵∠A和∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A比∠B的两倍少30°,
即∠A=2∠B﹣30°,
∴2∠B﹣30°=∠B或2∠B﹣30°+∠B=180°,
∴∠B=30°或∠B=70°
故答案为:30°或70°.
8.解:过点E作EF∥AB
∴∠α+∠AEF=180°(两直线平行,同旁内角互补)
∵AB∥CD(已知)
∴EF∥CD.
∴∠FED=∠EDC(两直线平行,内错角相等)
∵∠β=∠AEF+∠FED
又∵∠γ=∠EDC(已知)
∴∠α+∠β﹣∠γ=180°.
9.解:作EM∥AB,FN∥AB,
∵AB∥CD,
∴AB∥EM∥FN∥CD.
∴∠A+∠AEM=180°,∠MEF+∠EFN=180°,∠NFC+∠C=180°,
∴∠A+∠AEF+∠EFC+∠C=540°.
故答案为540°.
10.解:∵MA1与NAn平行,
∴在图①可得∠A1+∠A2=180°,
在②中可过A2作A2B∥MA1,如图.
∵MA1∥NA3,
∴A2B∥NA3,
∴∠MA1A2+∠BA2A1=∠BA2A3+∠NA3A2=180°,
∴∠A1+∠A2+∠A3=360°,
同理可得∠A1+∠A2+∠A3+∠A4=540°,
∵∠A1+∠A2=180°=1×180°,
∠A1+∠A2+∠A3=360°=2×180°,
∠A1+∠A2+∠A3+∠A4=540°=3×180°,
∴∠A1+∠A2+∠A3++…+∠A8=7×180°=1260°.
故答案为:1260°.
11.证明:(1)如图1,过点P作PQ∥l1,
∵PQ∥l1,
∴∠1=∠4(两直线平行,内错角相等),
∵PQ∥l1,l1∥l2(已知),
∴PQ∥l2(平行于同一条直线的两直线平行),
∴∠5=∠2(两直线平行,内错角相等),
∵∠3=∠4+∠5,
∴∠3=∠1+∠2(等量代换);
故答案为:∠3=∠1+∠2;
(2)∠1、∠2、∠3之间的关系不发生变化;
故答案为:∠3=∠1+∠2;
(3)∠1﹣∠2=∠3或∠2﹣∠1=∠3.
故答案为:∠1﹣∠2=∠3或∠2﹣∠1=∠3.
12.解:如右图所示,作PE∥CD,
∵PE∥CD,
∴∠C+∠CPE=180°,
又∵AB∥CD,
∴PE∥AB,
∴∠A=∠APE,
∴∠A+∠C﹣∠P=180°,
故答案为:∠A+∠C﹣∠P=180°.
13.解:∵∠2+60°+45°=180°,
∴∠2=75°.
∵直尺的上下两边平行,
∴∠1=∠2=75°.
故答案为:75.
14.解:过P作DE的平行线PQ,过D作AB的平行线DH,设∠ABF=∠CBF=y,∠EDP=∠CDP=x,
∵PQ∥AB
∴∠QPB=∠ABF=y,
∵PQ∥DE,∠BPD=44°
∴∠EDP=∠QPD=44°+y=x,
∴x﹣y=44°,
过C作DE的平行线CG,
∵CG∥AB∥DE
∴∠ABC=∠BCG,∠CDH=∠GCD,
∴∠BCD=∠BCG+∠GCD=∠ABC+∠CDH=2y+(180°﹣2x)=180°﹣44°×2=92°,
故答案为92°
15.解:∵AB∥PQ,
∴∠ABO=∠BOP=45°,
∵CD∥PQ,
∴∠DCO+∠QOC=180°,
即∠DCO+68°=180°,
解得∠DCO=112°.
故答案为:45°;112°.
16.解:∵AB∥CE,∠ABC=30°,
∴∠ABC=∠BCE=30°,
∵∠BDE=45°,
∴∠DBC=∠BDE﹣∠BCE=45°﹣30°=15°,
故答案为:15°.
17.解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=92°,
∴∠CFE=92°,
又∵∠DCE=115°,
∴∠E=∠DCE﹣∠CFE=115°﹣92°=23°.
故答案为:23.
18.解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DEF=∠1,∠AED′=∠BGD'=x度,
再根据对折,得:∠GEF=∠DEF,
再根据平角的定义,得:∠DEF=(180°﹣x°)÷2=度.
∴∠1=度.
故答案为:.
19.解:∵把一张长方形纸带沿着直线GF折叠,∠CGF=35°,
∴∠EGF=∠FGC=35°,
∵AD∥BC,
∴∠CGF=∠GFE=35°,
∴∠2=70°,
∵GE∥FH,
∴∠1=∠2=70°.
故答案为:70°.
20.解:如图,延长DE交AB的延长线于G,
∵AB∥CD,
∴∠D=∠AGD=40°,
∵BF∥DE,
∴∠AGD=∠ABF=40°,
∵BF平分∠ABE,
∴∠EBF=∠ABF=40°,
∵BF∥DE,
∴∠BED=180°﹣∠EBF=140°.
故答案为:140°.
21.解:如图所示,过M作MN∥a,
∵a∥b,
∴MN∥b,
根据平行线的性质:两条直线平行,内错角相等.得
∠1=∠AMN,∠2=∠BMN,
∴∠1+∠2=∠AMB=90°.
故填90.
22.解:过点C作CF∥AB,
已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,
∴AB∥DE,
∴CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=60°,
∴∠DCF=20°,
∴∠CDE=∠DCF=20°.
故答案为:20.
填空题优生辅导训练(附答案)
1.将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2= .
2.武侯祠博物馆享有“三国圣地”的美誉,它的大门的栏杆示意图如图所示,BA⊥AE于点A,CD∥AE,若∠BCD=120°,那么∠ABC= 度.
3.如图,AB∥CD,EF⊥BD,垂足为F,∠1=43°,则∠2的度数为 .
4.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的度数为 .
5.如图CD⊥AB于D,EF⊥AB于F,∠DGC=105°,∠BCG=75°,则∠1+∠2= .
6.如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠D=50°,则下列结论:①∠AOE=65°;②OF平分∠BOD;③∠GOE=∠DOF;④∠GOE=25°.其中正确说法的序号是 .
7.若∠A和∠B的两边分别平行,且∠A比∠B的两倍少30°,则∠B的度数是 .
8.已知,如图,AB∥CD,则∠α、∠β、∠γ之间的关系为 .
9.如图所示,AB∥CD,则∠A+∠E+∠F+∠C= .
10.如图①:MA1∥NA2,图②:MA1∥NA3,图③:MA1∥NA4,图④:MA1∥NA5,……,
则第7个图中的∠A1+∠A2+∠A3+…+∠A8= .
11.如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.
(1)∠1、∠2、∠3之间的关系为 ;
(2)如果点P在A、B两点之间运动时,∠1、∠2、∠3之间的关系为 ;
(3)如果点P(点P和A、B不重合)在A、B两点外侧运动时,∠1、∠2、∠3之间关系为 .
12.如图,已知AB∥CD,则∠A、∠C、∠P的关系为 .
13.将一副三角板(含30°、45°、60°、90°角)按如图所示的位置摆放在直尺上,则∠1的度数为 度.
14.如图AB∥DE,BF平分∠ABC,反向延长射线BF,与∠EDC的平分线DG相交于点P,若∠BPD=44°,则∠C= .
15.太阳灶、卫星信号接收锅、探照灯以及其他很多灯具都与抛物线有关.如图,从点O照射到抛物线上的光线OB,OC等反射以后沿着与POQ平行的方向射出.图中如果∠BOP=45°,∠QOC=68°,则∠ABO= ,∠DCO= .
16.如图,AB∥CE,∠ABC=30°,∠BDE=45°,则∠DBC= .
17.欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是 °.
18.如图,把一张长方形纸条ABCD沿EF折叠,若∠BGD'为x度,则∠1的度数应为 度(用含x的代数式表示).
19.如图,把一张长方形纸带沿着直线GF折叠,∠CGF=35°,则∠1的度数是 .
20.如图,已知AB∥CD,BF平分∠ABE,BF∥DE,且∠D=40°,则∠BED的度数为 .
21.如图,是我们生活中经常接触的小刀,刀片的外形是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2= 度.
22.珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE= 度.
参考答案
1.证明:如图,过点B作BN∥FG,
∵四边形EFGH是矩形纸片,
∴EH∥FG,
∴BN∥EH∥FG,
∴∠1=∠3,∠2=∠4,
∴∠1+∠2=∠3+∠4=∠ABC=90°,
即∠1+∠2=90°.
故答案为:90°.
2.解:过点B作BN∥AE,如图所示:
∵CD∥AE,
∴BN∥CD,
∴∠BCD+∠CBN=180°,
∴∠CBN=180°﹣∠BCD=180°﹣120°=60°,
∵BA⊥AE,
∴BN⊥BA,
∴∠ABN=90°,
∴∠ABC=∠CBN+∠ABN=60°+90°=150°,
故答案为:150.
3.解:∵AB∥CD,
∴∠D=∠1=43°.
∵EF⊥BD,垂足为F,
∴∠DFE=90°,
∴∠2=180°﹣90°﹣43°=47°.
故答案为:47°.
4.解:过点B作BD∥l,
∵直线l∥m,
∴BD∥l∥m,
∴∠4=∠1,∠2=∠3,
∴∠1+∠2=∠3+∠4=∠ABC,
∵∠ABC=45°,
∴∠1+∠2=45°.
故答案为:45°.
5.解:∵∠DGC=105°,∠BCG=75°(已知),
∴∠DGC+∠BCG=180°,
∴DG∥BC(同旁内角互补,两直线平行),
∴∠1=∠DCB(两直线平行,内错角相等),
∵CD⊥AB,EF⊥AB(已知),
∴CD∥EF(平面内,垂直于同一直线的两直线平行),
∴∠DCB+∠2=180°(两直线平行,同旁内角互补),
∴∠1+∠2=180°(等量代换),
故答案为:180°.
6.解:∵AB∥CD,
∴∠BOD=∠CDO=50°,
∴∠AOD=180°﹣50°=130°,
又∵OE平分∠AOD,
∴∠AOE=∠AOD=65°,
故①正确;
∵OG⊥CD,
∴∠GOA=∠DGO=90°,
∴∠GOD=40°,∠GOE=90°﹣∠AOE=25°,
∴∠EOG+∠GOD=65°,
又OE⊥OF,
∴∠DOF=25°,
∴∠BOF=∠DOF=25°,
∴OF平分∠BOD,∠GOE=∠DOF,故②③④正确;
故答案是:①②③④.
7.解:∵∠A和∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A比∠B的两倍少30°,
即∠A=2∠B﹣30°,
∴2∠B﹣30°=∠B或2∠B﹣30°+∠B=180°,
∴∠B=30°或∠B=70°
故答案为:30°或70°.
8.解:过点E作EF∥AB
∴∠α+∠AEF=180°(两直线平行,同旁内角互补)
∵AB∥CD(已知)
∴EF∥CD.
∴∠FED=∠EDC(两直线平行,内错角相等)
∵∠β=∠AEF+∠FED
又∵∠γ=∠EDC(已知)
∴∠α+∠β﹣∠γ=180°.
9.解:作EM∥AB,FN∥AB,
∵AB∥CD,
∴AB∥EM∥FN∥CD.
∴∠A+∠AEM=180°,∠MEF+∠EFN=180°,∠NFC+∠C=180°,
∴∠A+∠AEF+∠EFC+∠C=540°.
故答案为540°.
10.解:∵MA1与NAn平行,
∴在图①可得∠A1+∠A2=180°,
在②中可过A2作A2B∥MA1,如图.
∵MA1∥NA3,
∴A2B∥NA3,
∴∠MA1A2+∠BA2A1=∠BA2A3+∠NA3A2=180°,
∴∠A1+∠A2+∠A3=360°,
同理可得∠A1+∠A2+∠A3+∠A4=540°,
∵∠A1+∠A2=180°=1×180°,
∠A1+∠A2+∠A3=360°=2×180°,
∠A1+∠A2+∠A3+∠A4=540°=3×180°,
∴∠A1+∠A2+∠A3++…+∠A8=7×180°=1260°.
故答案为:1260°.
11.证明:(1)如图1,过点P作PQ∥l1,
∵PQ∥l1,
∴∠1=∠4(两直线平行,内错角相等),
∵PQ∥l1,l1∥l2(已知),
∴PQ∥l2(平行于同一条直线的两直线平行),
∴∠5=∠2(两直线平行,内错角相等),
∵∠3=∠4+∠5,
∴∠3=∠1+∠2(等量代换);
故答案为:∠3=∠1+∠2;
(2)∠1、∠2、∠3之间的关系不发生变化;
故答案为:∠3=∠1+∠2;
(3)∠1﹣∠2=∠3或∠2﹣∠1=∠3.
故答案为:∠1﹣∠2=∠3或∠2﹣∠1=∠3.
12.解:如右图所示,作PE∥CD,
∵PE∥CD,
∴∠C+∠CPE=180°,
又∵AB∥CD,
∴PE∥AB,
∴∠A=∠APE,
∴∠A+∠C﹣∠P=180°,
故答案为:∠A+∠C﹣∠P=180°.
13.解:∵∠2+60°+45°=180°,
∴∠2=75°.
∵直尺的上下两边平行,
∴∠1=∠2=75°.
故答案为:75.
14.解:过P作DE的平行线PQ,过D作AB的平行线DH,设∠ABF=∠CBF=y,∠EDP=∠CDP=x,
∵PQ∥AB
∴∠QPB=∠ABF=y,
∵PQ∥DE,∠BPD=44°
∴∠EDP=∠QPD=44°+y=x,
∴x﹣y=44°,
过C作DE的平行线CG,
∵CG∥AB∥DE
∴∠ABC=∠BCG,∠CDH=∠GCD,
∴∠BCD=∠BCG+∠GCD=∠ABC+∠CDH=2y+(180°﹣2x)=180°﹣44°×2=92°,
故答案为92°
15.解:∵AB∥PQ,
∴∠ABO=∠BOP=45°,
∵CD∥PQ,
∴∠DCO+∠QOC=180°,
即∠DCO+68°=180°,
解得∠DCO=112°.
故答案为:45°;112°.
16.解:∵AB∥CE,∠ABC=30°,
∴∠ABC=∠BCE=30°,
∵∠BDE=45°,
∴∠DBC=∠BDE﹣∠BCE=45°﹣30°=15°,
故答案为:15°.
17.解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=92°,
∴∠CFE=92°,
又∵∠DCE=115°,
∴∠E=∠DCE﹣∠CFE=115°﹣92°=23°.
故答案为:23.
18.解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DEF=∠1,∠AED′=∠BGD'=x度,
再根据对折,得:∠GEF=∠DEF,
再根据平角的定义,得:∠DEF=(180°﹣x°)÷2=度.
∴∠1=度.
故答案为:.
19.解:∵把一张长方形纸带沿着直线GF折叠,∠CGF=35°,
∴∠EGF=∠FGC=35°,
∵AD∥BC,
∴∠CGF=∠GFE=35°,
∴∠2=70°,
∵GE∥FH,
∴∠1=∠2=70°.
故答案为:70°.
20.解:如图,延长DE交AB的延长线于G,
∵AB∥CD,
∴∠D=∠AGD=40°,
∵BF∥DE,
∴∠AGD=∠ABF=40°,
∵BF平分∠ABE,
∴∠EBF=∠ABF=40°,
∵BF∥DE,
∴∠BED=180°﹣∠EBF=140°.
故答案为:140°.
21.解:如图所示,过M作MN∥a,
∵a∥b,
∴MN∥b,
根据平行线的性质:两条直线平行,内错角相等.得
∠1=∠AMN,∠2=∠BMN,
∴∠1+∠2=∠AMB=90°.
故填90.
22.解:过点C作CF∥AB,
已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,
∴AB∥DE,
∴CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=60°,
∴∠DCF=20°,
∴∠CDE=∠DCF=20°.
故答案为:20.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
