8.2.2 一元线性回归模型参数的最小二乘估计同步训练-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(word含解析)
文档属性
| 名称 | 8.2.2 一元线性回归模型参数的最小二乘估计同步训练-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(word含解析) | 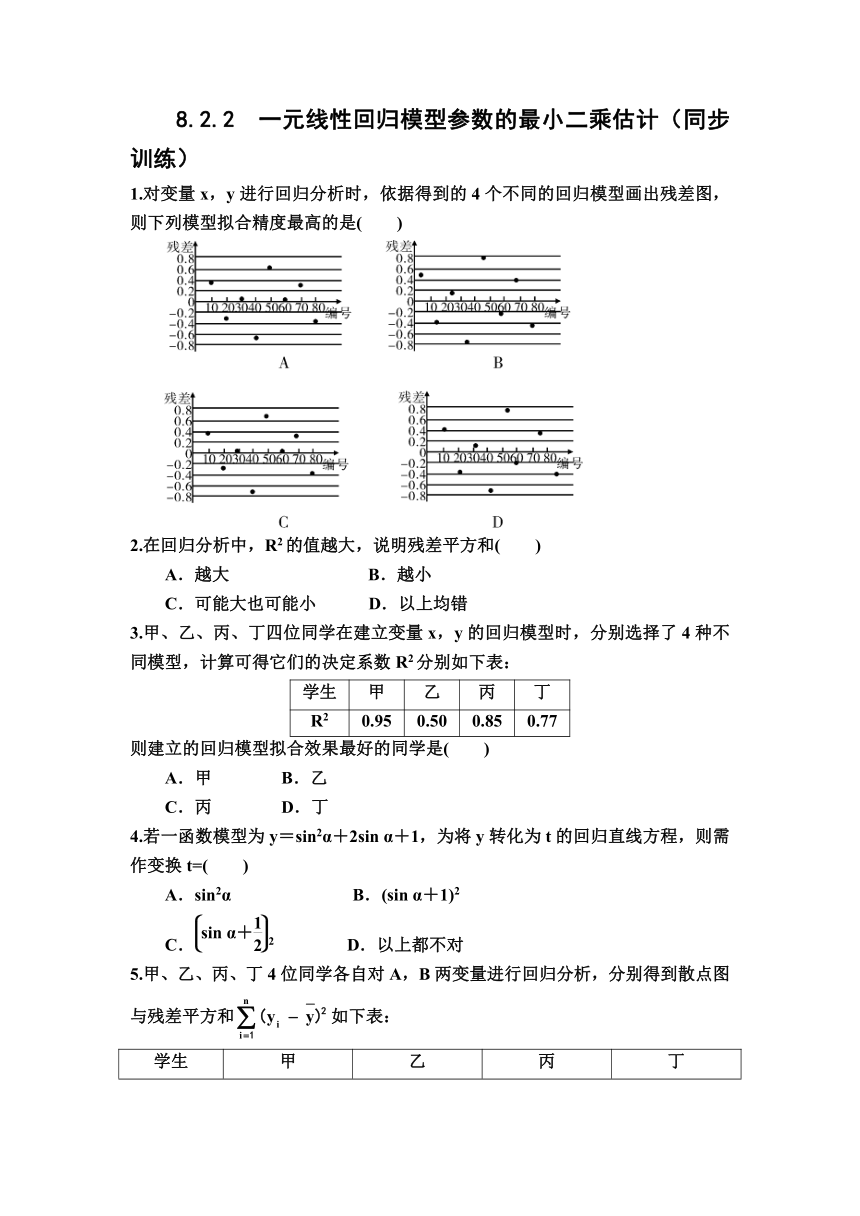 | |
| 格式 | docx | ||
| 文件大小 | 85.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 09:40:38 | ||
图片预览



文档简介
8.2.2 一元线性回归模型参数的最小二乘估计(同步训练)
1.对变量x,y进行回归分析时,依据得到的4个不同的回归模型画出残差图,则下列模型拟合精度最高的是( )
2.在回归分析中,R2的值越大,说明残差平方和( )
A.越大 B.越小
C.可能大也可能小 D.以上均错
3.甲、乙、丙、丁四位同学在建立变量x,y的回归模型时,分别选择了4种不同模型,计算可得它们的决定系数R2分别如下表:
学生 甲 乙 丙 丁
R2 0.95 0.50 0.85 0.77
则建立的回归模型拟合效果最好的同学是( )
A.甲 B.乙
C.丙 D.丁
4.若一函数模型为y=sin2α+2sin α+1,为将y转化为t的回归直线方程,则需作变换t=( )
A.sin2α B.(sin α+1)2
C.2 D.以上都不对
5.甲、乙、丙、丁4位同学各自对A,B两变量进行回归分析,分别得到散点图与残差平方和如下表:
学生 甲 乙 丙 丁
散点图
残差平方和 115 106 124 103
哪位同学的试验结果体现拟合A,B两变量关系的模型拟合精度高( )
A.甲 B.乙 C.丙 D.丁
2020年初,新冠肺炎疫情暴发以来,各地医疗机构采取了各种针对性的治疗方法,取得了不错的成效,某地开始使用中西医结合方法后,每周治愈的患者人数如表所示:
周数x 1 2 3 4 5
治愈人数y 2 17 36 103 142
由表格可得y关于x的非线性经验回归方程为=6x2+,则此回归模型第4周的残差为( )
A.13 B.-13
C.5 D.-5
7.已知变量y关于x的非线性经验回归方程为=ex-0.5,其一组数据如下表所示:
x 1 2 3 4
y e e3 e4 e6
若x=5,则预测y的值可能为( )
A.e5 B.
C.e7 D.
8.某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润额y/百万元 2 3 3 4 5
已知y关于x的经验回归方程为=0.5x+0.4,则当销售额为5千万元时,残差为________
9.以模型y=cekx去拟合一组数据时,为了求出回归方程,设z=ln y,其变换后得到线性回归方程z=0.3x+4,则c=________
10.对两个具有非线性相关关系的变量x,y进行回归分析,设μ=ln y,υ=(x-4)2,利用二乘法得到μ关于υ的经验回归方程为μ=-0.5υ+2,则的最大值是________
11.某电视厂家准备在元旦举行促销活动,现根据近七年的广告费与销售量的数据确定此次广告费支出.广告费支出x(单位:万元)和销售量y(单位:万台)的数据如下:
年份 2014 2015 2016 2017 2018 2019 2020
广告费支出x 1 2 4 6 11 13 19
销售量y 1.9 3.2 4.0 4.4 5.2 5.3 5.4
(1)若用线性回归模型拟合y与x的关系,求出y关于x的线性回归方程;
(2)若用y=c+d模型拟合y与x的关系,可得回归方程=1.63+0.99,经计算线性回归模型和该模型的R2分别约为0.75和0.88,请用R2说明选择哪个回归模型更好.
12.BMI指数是用体重公斤数除以身高米数的平方得出的数值,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.在我国,BMI<18.5,认为体重过轻;18.5≤BMI<24,认为体重正常;BMI≥24,认为体重超重.某中小学生成长与发展机构从某市的320名高中男体育特长生中随机选取8名,其身高和体重的数据如下表所示:
编号 1 2 3 4 5 6 7 8
身高x/cm 166 167 160 173 178 169 158 173
体重y/kg 57 58 53 61 66 57 50 66
(1)根据最小二乘法求得的经验回归方程为=0.8x-75.9,利用已经求得的经验回归方程完善下列残差表,并求变化的贡献值R2(保留两位有效数字);
编号 1 2 3 4 5 6 7 8
身高x/cm 166 167 160 173 178 169 158 173
体重y/kg 57 58 53 61 66 57 50 66
残差 0.1 0.3 0.9 -1.5 -0.5
(2)通过残差分析,对于残差最大(绝对值)的那组数据,需要确认在样本点的采集中是否有人为的错误.已知通过重新采集发现,该组数据的体重应该为58 kg.请重新根据最小二乘法,求出y关于x的经验回归方程.
参考数据:=78 880,=226 112,=168,=58.5,=226.
参考答案:
1.A
解析:用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
2.B
解析:因为R2=,所以当R2越大时,越小,即残差平方和越小.
3.A 解析:R2越大,表示回归模型的拟合效果越好.
4.B
解析:因为y是关于t的回归直线方程,实际上就是y关于t的一次函数,又因为y=(sin α+1)2,若令t=(sin α+1)2,则可得y与t的函数关系式为y=t,此时变量y与变量t是线性相关关系.
5.D
解析:根据线性相关的知识,散点图中各样本点条状分布越均匀,同时保持残差平方和越小,则由回归分析建立的线性回归模型的拟合效果越好,由试验结果知丁要好些.
6.A
解析:因为2=(1+4+9+16+25)=11, =(2+17+36+103+142)=60,所以=60-6×11=-6,则y关于x的非线性经验回归方程为=6x2-6.取x=4,得=6×42-6=90,所以此回归模型第4周的预报值为90,则此回归模型第4周的残差为103-90=13.
7.D
解析:将式子两边取对数,得到ln =x-0.5.令z=ln ,得到z=x-0.5,列出x,z的取值对应的表格如下:
x 1 2 3 4
z 1 3 4 6
则==2.5,==3.5.∵(,)满足z=x-0.5,∴3.5=×2.5-0.5,解得=1.6,∴z=1.6x-0.5,∴=e1.6x-0.5.当x=5时,=e1.6×5-0.5=e.
8.答案:0.1
解析:当x=5时,=0.5×5+0.4=2.9,表格中对应y=3,于是残差为3-2.9=0.1.
9.答案:e4
解析:由题意,得ln(cekx)=0.3x+4,所以ln c+kx=0.3x+4,比较两边系数,得ln c=4,所以c=e4.
10.答案:e2
解析:将μ=ln y,υ=(x-4)2代入经验回归方程μ=-0.5υ+2,得=e-0.5(x-4)2+2.
当x=4时,=e-0.5(4-4)2+2=e2,故最大值为e2.
11.解:(1)∵=8,=4.2,=279.4,=708,
∴===0.17,
=-=4.2-0.17×8=2.84,
∴y关于x的线性回归方程为=0.17x+2.84.
(2)∵0.75<0.88且R2越大,反映残差平方和越小,模型的拟合效果越好,∴选用=1.63+0.99更好.
12.解:(1)由题知经验回归方程为=0.8x-75.9,则6=57-0.8×169+75.9=-2.3,7=50-0.8×158+75.9=-0.5,8=66-0.8×173+75.9=3.5.完善残差表如下:
编号 1 2 3 4 5 6 7 8
身高x/cm 166 167 160 173 178 169 158 173
体重y/kg 57 58 53 61 66 57 50 66
残差 0.1 0.3 0.9 -1.5 -0.5 -2.3 -0.5 3.5
R2==1-×(0.01+0.09+0.81+2.25+0.25+5.29+0.25+12.25)≈0.91.
(2)通过残差分析知,残差最大(绝对值)的那组数据为第8组,所以y8=58,
所以修改后=78 880-173×66+173×58=77 496,
=×(8×58.5-66+58)=57.5,
所以===0.675,
=-=57.5-0.675×168=-55.9.
所以y关于x的经验回归方程=0.675x-55.9.
1.对变量x,y进行回归分析时,依据得到的4个不同的回归模型画出残差图,则下列模型拟合精度最高的是( )
2.在回归分析中,R2的值越大,说明残差平方和( )
A.越大 B.越小
C.可能大也可能小 D.以上均错
3.甲、乙、丙、丁四位同学在建立变量x,y的回归模型时,分别选择了4种不同模型,计算可得它们的决定系数R2分别如下表:
学生 甲 乙 丙 丁
R2 0.95 0.50 0.85 0.77
则建立的回归模型拟合效果最好的同学是( )
A.甲 B.乙
C.丙 D.丁
4.若一函数模型为y=sin2α+2sin α+1,为将y转化为t的回归直线方程,则需作变换t=( )
A.sin2α B.(sin α+1)2
C.2 D.以上都不对
5.甲、乙、丙、丁4位同学各自对A,B两变量进行回归分析,分别得到散点图与残差平方和如下表:
学生 甲 乙 丙 丁
散点图
残差平方和 115 106 124 103
哪位同学的试验结果体现拟合A,B两变量关系的模型拟合精度高( )
A.甲 B.乙 C.丙 D.丁
2020年初,新冠肺炎疫情暴发以来,各地医疗机构采取了各种针对性的治疗方法,取得了不错的成效,某地开始使用中西医结合方法后,每周治愈的患者人数如表所示:
周数x 1 2 3 4 5
治愈人数y 2 17 36 103 142
由表格可得y关于x的非线性经验回归方程为=6x2+,则此回归模型第4周的残差为( )
A.13 B.-13
C.5 D.-5
7.已知变量y关于x的非线性经验回归方程为=ex-0.5,其一组数据如下表所示:
x 1 2 3 4
y e e3 e4 e6
若x=5,则预测y的值可能为( )
A.e5 B.
C.e7 D.
8.某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润额y/百万元 2 3 3 4 5
已知y关于x的经验回归方程为=0.5x+0.4,则当销售额为5千万元时,残差为________
9.以模型y=cekx去拟合一组数据时,为了求出回归方程,设z=ln y,其变换后得到线性回归方程z=0.3x+4,则c=________
10.对两个具有非线性相关关系的变量x,y进行回归分析,设μ=ln y,υ=(x-4)2,利用二乘法得到μ关于υ的经验回归方程为μ=-0.5υ+2,则的最大值是________
11.某电视厂家准备在元旦举行促销活动,现根据近七年的广告费与销售量的数据确定此次广告费支出.广告费支出x(单位:万元)和销售量y(单位:万台)的数据如下:
年份 2014 2015 2016 2017 2018 2019 2020
广告费支出x 1 2 4 6 11 13 19
销售量y 1.9 3.2 4.0 4.4 5.2 5.3 5.4
(1)若用线性回归模型拟合y与x的关系,求出y关于x的线性回归方程;
(2)若用y=c+d模型拟合y与x的关系,可得回归方程=1.63+0.99,经计算线性回归模型和该模型的R2分别约为0.75和0.88,请用R2说明选择哪个回归模型更好.
12.BMI指数是用体重公斤数除以身高米数的平方得出的数值,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.在我国,BMI<18.5,认为体重过轻;18.5≤BMI<24,认为体重正常;BMI≥24,认为体重超重.某中小学生成长与发展机构从某市的320名高中男体育特长生中随机选取8名,其身高和体重的数据如下表所示:
编号 1 2 3 4 5 6 7 8
身高x/cm 166 167 160 173 178 169 158 173
体重y/kg 57 58 53 61 66 57 50 66
(1)根据最小二乘法求得的经验回归方程为=0.8x-75.9,利用已经求得的经验回归方程完善下列残差表,并求变化的贡献值R2(保留两位有效数字);
编号 1 2 3 4 5 6 7 8
身高x/cm 166 167 160 173 178 169 158 173
体重y/kg 57 58 53 61 66 57 50 66
残差 0.1 0.3 0.9 -1.5 -0.5
(2)通过残差分析,对于残差最大(绝对值)的那组数据,需要确认在样本点的采集中是否有人为的错误.已知通过重新采集发现,该组数据的体重应该为58 kg.请重新根据最小二乘法,求出y关于x的经验回归方程.
参考数据:=78 880,=226 112,=168,=58.5,=226.
参考答案:
1.A
解析:用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
2.B
解析:因为R2=,所以当R2越大时,越小,即残差平方和越小.
3.A 解析:R2越大,表示回归模型的拟合效果越好.
4.B
解析:因为y是关于t的回归直线方程,实际上就是y关于t的一次函数,又因为y=(sin α+1)2,若令t=(sin α+1)2,则可得y与t的函数关系式为y=t,此时变量y与变量t是线性相关关系.
5.D
解析:根据线性相关的知识,散点图中各样本点条状分布越均匀,同时保持残差平方和越小,则由回归分析建立的线性回归模型的拟合效果越好,由试验结果知丁要好些.
6.A
解析:因为2=(1+4+9+16+25)=11, =(2+17+36+103+142)=60,所以=60-6×11=-6,则y关于x的非线性经验回归方程为=6x2-6.取x=4,得=6×42-6=90,所以此回归模型第4周的预报值为90,则此回归模型第4周的残差为103-90=13.
7.D
解析:将式子两边取对数,得到ln =x-0.5.令z=ln ,得到z=x-0.5,列出x,z的取值对应的表格如下:
x 1 2 3 4
z 1 3 4 6
则==2.5,==3.5.∵(,)满足z=x-0.5,∴3.5=×2.5-0.5,解得=1.6,∴z=1.6x-0.5,∴=e1.6x-0.5.当x=5时,=e1.6×5-0.5=e.
8.答案:0.1
解析:当x=5时,=0.5×5+0.4=2.9,表格中对应y=3,于是残差为3-2.9=0.1.
9.答案:e4
解析:由题意,得ln(cekx)=0.3x+4,所以ln c+kx=0.3x+4,比较两边系数,得ln c=4,所以c=e4.
10.答案:e2
解析:将μ=ln y,υ=(x-4)2代入经验回归方程μ=-0.5υ+2,得=e-0.5(x-4)2+2.
当x=4时,=e-0.5(4-4)2+2=e2,故最大值为e2.
11.解:(1)∵=8,=4.2,=279.4,=708,
∴===0.17,
=-=4.2-0.17×8=2.84,
∴y关于x的线性回归方程为=0.17x+2.84.
(2)∵0.75<0.88且R2越大,反映残差平方和越小,模型的拟合效果越好,∴选用=1.63+0.99更好.
12.解:(1)由题知经验回归方程为=0.8x-75.9,则6=57-0.8×169+75.9=-2.3,7=50-0.8×158+75.9=-0.5,8=66-0.8×173+75.9=3.5.完善残差表如下:
编号 1 2 3 4 5 6 7 8
身高x/cm 166 167 160 173 178 169 158 173
体重y/kg 57 58 53 61 66 57 50 66
残差 0.1 0.3 0.9 -1.5 -0.5 -2.3 -0.5 3.5
R2==1-×(0.01+0.09+0.81+2.25+0.25+5.29+0.25+12.25)≈0.91.
(2)通过残差分析知,残差最大(绝对值)的那组数据为第8组,所以y8=58,
所以修改后=78 880-173×66+173×58=77 496,
=×(8×58.5-66+58)=57.5,
所以===0.675,
=-=57.5-0.675×168=-55.9.
所以y关于x的经验回归方程=0.675x-55.9.
