人教版2022年八年级下册18.2.1矩形 同步训练卷(word版,含解析)
文档属性
| 名称 | 人教版2022年八年级下册18.2.1矩形 同步训练卷(word版,含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 18:12:02 | ||
图片预览



文档简介
人教版2022年八年级下册18.2.1矩形 同步训练卷
一.选择题
1.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是
A.测量对角线是否相互平分
B.测量其中三个角是否都为直角
C.测量对角线是否相等
D.测量两组对边是否分别相等
2.矩形具有而平行四边形不一定具有的性质是
A.两组对边分别相等 B.对角线相等
C.两组对边分别平行 D.对角线互相平分
3.如图,四边形是平行四边形,两条对角线交于点,下列条件中,不能判定平行四边形为矩形的是
A. B. C. D.
4.在矩形中,,,两对角线交于点,则
A.3 B.4 C.5 D.10
5.如图,在矩形中,点是上一点,且,,垂足为点,在下列结论中,不一定正确的是
A. B. C. D.
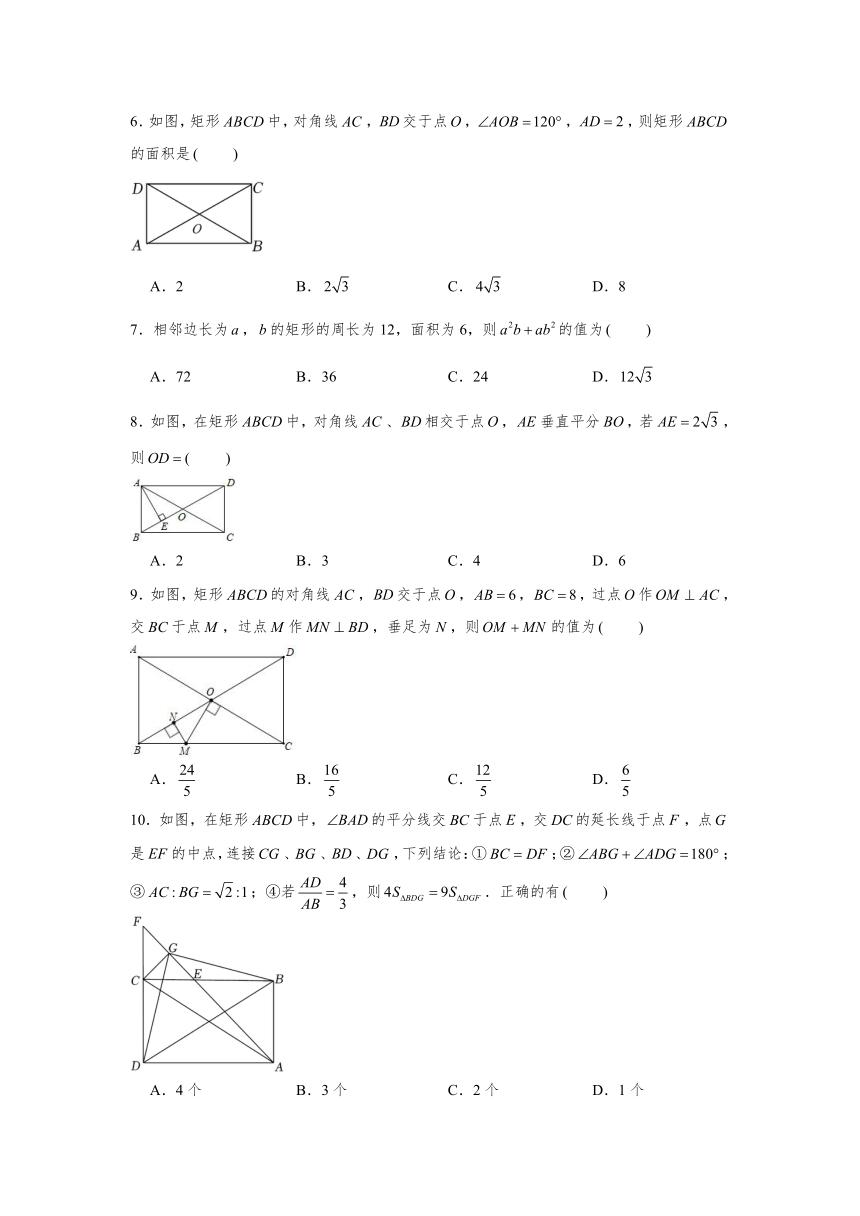
6.如图,矩形中,对角线,交于点,,,则矩形的面积是
A.2 B. C. D.8
7.相邻边长为,的矩形的周长为12,面积为6,则的值为
A.72 B.36 C.24 D.
8.如图,在矩形中,对角线、相交于点,垂直平分,若,则
A.2 B.3 C.4 D.6
9.如图,矩形的对角线,交于点,,,过点作,交于点,过点作,垂足为,则的值为
A. B. C. D.
10.如图,在矩形中,的平分线交于点,交的延长线于点,点是的中点,连接、、、,下列结论:①;②;③;④若,则.正确的有
A.4个 B.3个 C.2个 D.1个
二.填空题
11.如图,请添加一个条件使平行四边形成为矩形,这个条件可以是 (写出一种情况即可).
12.小华从商店购买了一块玻璃的示意图如下图所示,小华想检验这块玻璃的形状是否为矩形,设计如下几个方案:
①检验与是否相等,与是否相等.
②检验,是否为直角,与是否相等.
③检验,是否为直角,与是否相等.
④检验,是否为直角,与是否相等.
则可以检测出这块玻璃的形状是否为矩形的方案有 .
13.若矩形的周长为,对角线的长是,则它的面积是 .
14.如图在矩形中,对角线,相交于点,,分别是,的中点,若,,则 .
15.如图,在矩形中,,,为上一点,平分,则的长为 .
16.如图,矩形的对角线,交于点,在边上,连接并延长交边于点.若,,,则矩形的面积为 .
三.解答题
17.在中,过点作于点,点在边上,,连接,.求证:四边形是矩形.
18.如图,在四边形中,.点、、分别在边、、上,.
(1)求证:四边形是平行四边形;
(2)当与满足怎样的关系时,四边形是矩形.请说明理由.
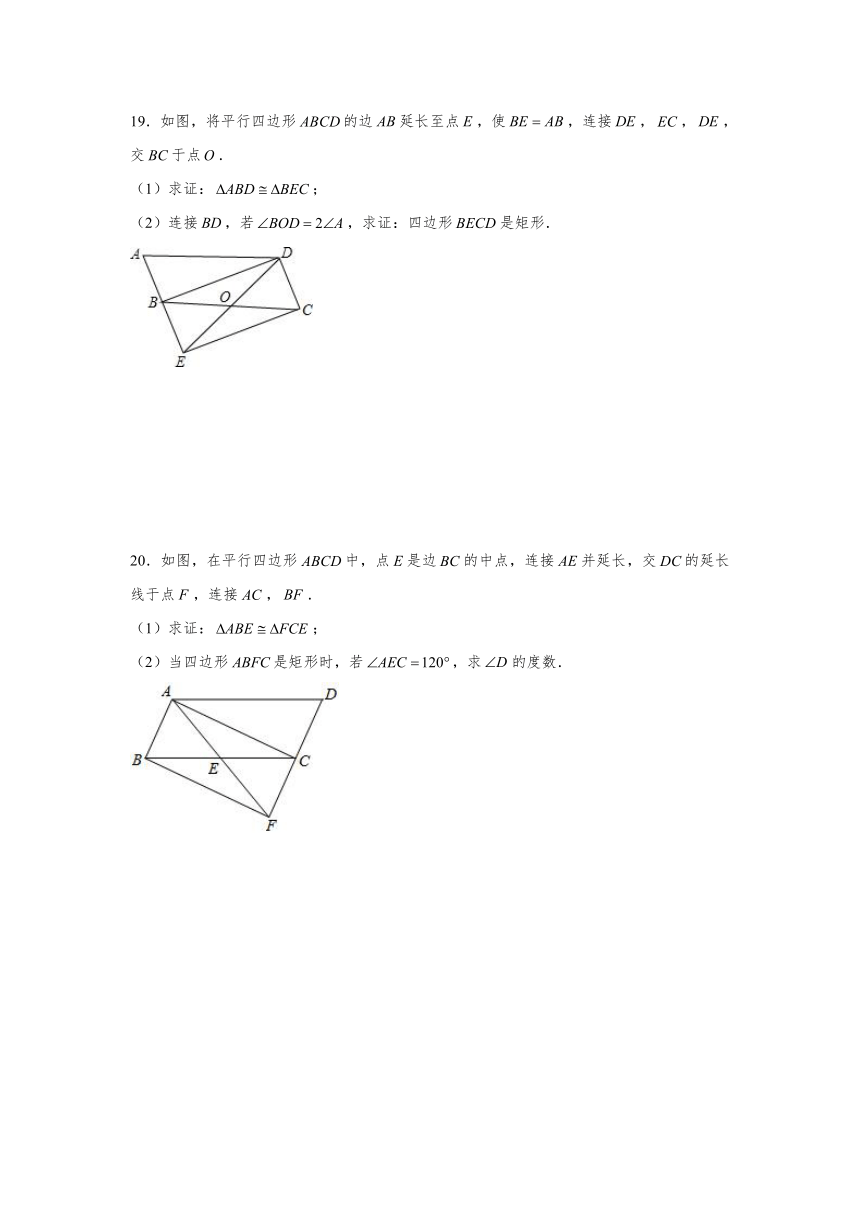
19.如图,将平行四边形的边延长至点,使,连接,,,交于点.
(1)求证:;
(2)连接,若,求证:四边形是矩形.
20.如图,在平行四边形中,点是边的中点,连接并延长,交的延长线于点,连接,.
(1)求证:;
(2)当四边形是矩形时,若,求的度数.
21.如图1,已知矩形中,,动点从点出发,沿方向以每秒1个单位的速度运动,连接,作点关于直线的对称点,设点运动时间.
(1)如图2,若,当点落在对角线上时,求的值;
(2)如图3,点、分别在边、边上,且,在动点沿射线上运动的过程中,求使点恰好落在直线上时对应的的值.
参考答案
一.选择题(共10小题)
1.解:、对角线是否相互平分,能判定平行四边形;
、其中四边形中三个角都为直角,能判定矩形;
、对角线相等的四边形不一定是矩形,不能判定形状;
、两组对边是否分别相等,能判定平行四边形.
故选:.
2.解:矩形的性质有两组对边平行且相等,对角线互相平分且相等,平行四边形的性质有两组对边平行且相等,对角线互相平分,
故选:.
3.解:、四边形是平行四边形,
,
,
,
,
平行四边形为矩形,故选项不符合题意;
、四边形是平行四边形,
,
不能判定平行四边形为矩形,故选项符合题意;
、四边形是平行四边形,
,,
,
,
平行四边形为矩形,故选项不符合题意;
、四边形是平行四边形,
,,
,
,
平行四边形为矩形,故选项不符合题意;
故选:.
4.解:四边形是矩形,
,,,
,
;
故选:.
5.解:、由矩形,可得,,
.
又,
,故正确;
、由,可得,
由矩形,可得,
又,
,故正确;
、由,可得,
由矩形,可得,
,故正确;
、不一定等于,
直角三角形中,不一定等于的一半,故错误;
故选:.
6.解:四边形是矩形,
,,
,
,
,
,
矩形的面积,
故选:.
7.解:相邻边长为,的矩形的周长为12,面积为6,
,,
则
.
故选:.
8.解:四边形是矩形,
,,,
,
垂直平分,
,
,
,
,
;
故选:.
9.解:,,
,
四边形是矩形,
,,,
,
,
,
,
,
,
故选:.
10.解:四边形是矩形,
,,,,
平分,
,
,
,
,故①正确;
,
,
故②正确;
四边形是矩形,
,
点为的中点,
,,
,
在和中,
,
.
,,
,
是等腰直角三角形,
,
,
,故③正确;
过点作于,
,
设,,
,,
,是等腰直角三角形,
,,
,,
;故④错误;
故选:.
二.填空题(共6小题)
11.解:若使平行四边形变为矩形,可添加的条件是:
;(对角线相等的平行四边形是矩形)
.(有一个角是直角的平行四边形是矩形)
故答案为:或.
12.解:①两组对边分别相等的四边形为平行四边形.
②一组对边平行且相等的四边形是平行四边形,一个角是直角的平行四边形是矩形.
③易证:
,
一组对边平行且相等的四边形是平行四边形,
一个角是直角或对角线相等的平行四边形是矩形.
④易证:,
,
两组对边分别相等的四边形是平行四边形,
一个角是直角的平行四边形是矩形,
故答案为②③④.
13.解:设,,
矩形周长为,
,
,
对角线的长是,
,
,
,
,
矩形面积为.
故答案为:.
14.解:在中,,
矩形中,,,
点、分别是、的中点,
是的中位线,
,
故答案为:5.
15.解:四边形是矩形,
,
,
平分,
,
,
,
在直角中,,
.
故答案为1.
16.解:如图,过点作于,
四边形是矩形,
,,,,
,,
在和中,
,
,
,
,,
,,
,,
,
,
,,
,
矩形的面积,
故答案为:.
三.解答题(共5小题)
17.证明:四边形是平行四边形,
,
,,
四边形是平行四边形,
,
,
四边形是矩形.
18.(1)证明:在四边形中,,
,
,,
,
即,
,
四边形是平行四边形.
(2)解:当时,四边形是矩形,
理由:,,,
,
.
.
四边形是平行四边形,
四边形是矩形.
19.证明:(1)在平行四边形中,,,,则.
又,
,
四边形为平行四边形,
.
在与中,
,
;
(2)由(1)知,四边形为平行四边形,则,.
四边形为平行四边形,
,即.
又,,
,
,
,即,
平行四边形为矩形.
20.(1)证明:四边形是平行四边形,
即,
,
点是的中点,
,
在和中,
,
;
(2)解:四边形是矩形,
,,,
,
,
,
,
四边形是平行四边形,
.
21.解:(1)如图2,连接,
,,
,
点关于直线的对称点,
,,,
,
,
;
(2)如图3,当点在线段上时,
点关于直线的对称点,
,,,
,
,
,
,
;
如图4,当点在线段的延长线上时,
点关于直线的对称点,
,,,
,
,
,
,
,
综上所述:或15.
一.选择题
1.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是
A.测量对角线是否相互平分
B.测量其中三个角是否都为直角
C.测量对角线是否相等
D.测量两组对边是否分别相等
2.矩形具有而平行四边形不一定具有的性质是
A.两组对边分别相等 B.对角线相等
C.两组对边分别平行 D.对角线互相平分
3.如图,四边形是平行四边形,两条对角线交于点,下列条件中,不能判定平行四边形为矩形的是
A. B. C. D.
4.在矩形中,,,两对角线交于点,则
A.3 B.4 C.5 D.10
5.如图,在矩形中,点是上一点,且,,垂足为点,在下列结论中,不一定正确的是
A. B. C. D.
6.如图,矩形中,对角线,交于点,,,则矩形的面积是
A.2 B. C. D.8
7.相邻边长为,的矩形的周长为12,面积为6,则的值为
A.72 B.36 C.24 D.
8.如图,在矩形中,对角线、相交于点,垂直平分,若,则
A.2 B.3 C.4 D.6
9.如图,矩形的对角线,交于点,,,过点作,交于点,过点作,垂足为,则的值为
A. B. C. D.
10.如图,在矩形中,的平分线交于点,交的延长线于点,点是的中点,连接、、、,下列结论:①;②;③;④若,则.正确的有
A.4个 B.3个 C.2个 D.1个
二.填空题
11.如图,请添加一个条件使平行四边形成为矩形,这个条件可以是 (写出一种情况即可).
12.小华从商店购买了一块玻璃的示意图如下图所示,小华想检验这块玻璃的形状是否为矩形,设计如下几个方案:
①检验与是否相等,与是否相等.
②检验,是否为直角,与是否相等.
③检验,是否为直角,与是否相等.
④检验,是否为直角,与是否相等.
则可以检测出这块玻璃的形状是否为矩形的方案有 .
13.若矩形的周长为,对角线的长是,则它的面积是 .
14.如图在矩形中,对角线,相交于点,,分别是,的中点,若,,则 .
15.如图,在矩形中,,,为上一点,平分,则的长为 .
16.如图,矩形的对角线,交于点,在边上,连接并延长交边于点.若,,,则矩形的面积为 .
三.解答题
17.在中,过点作于点,点在边上,,连接,.求证:四边形是矩形.
18.如图,在四边形中,.点、、分别在边、、上,.
(1)求证:四边形是平行四边形;
(2)当与满足怎样的关系时,四边形是矩形.请说明理由.
19.如图,将平行四边形的边延长至点,使,连接,,,交于点.
(1)求证:;
(2)连接,若,求证:四边形是矩形.
20.如图,在平行四边形中,点是边的中点,连接并延长,交的延长线于点,连接,.
(1)求证:;
(2)当四边形是矩形时,若,求的度数.
21.如图1,已知矩形中,,动点从点出发,沿方向以每秒1个单位的速度运动,连接,作点关于直线的对称点,设点运动时间.
(1)如图2,若,当点落在对角线上时,求的值;
(2)如图3,点、分别在边、边上,且,在动点沿射线上运动的过程中,求使点恰好落在直线上时对应的的值.
参考答案
一.选择题(共10小题)
1.解:、对角线是否相互平分,能判定平行四边形;
、其中四边形中三个角都为直角,能判定矩形;
、对角线相等的四边形不一定是矩形,不能判定形状;
、两组对边是否分别相等,能判定平行四边形.
故选:.
2.解:矩形的性质有两组对边平行且相等,对角线互相平分且相等,平行四边形的性质有两组对边平行且相等,对角线互相平分,
故选:.
3.解:、四边形是平行四边形,
,
,
,
,
平行四边形为矩形,故选项不符合题意;
、四边形是平行四边形,
,
不能判定平行四边形为矩形,故选项符合题意;
、四边形是平行四边形,
,,
,
,
平行四边形为矩形,故选项不符合题意;
、四边形是平行四边形,
,,
,
,
平行四边形为矩形,故选项不符合题意;
故选:.
4.解:四边形是矩形,
,,,
,
;
故选:.
5.解:、由矩形,可得,,
.
又,
,故正确;
、由,可得,
由矩形,可得,
又,
,故正确;
、由,可得,
由矩形,可得,
,故正确;
、不一定等于,
直角三角形中,不一定等于的一半,故错误;
故选:.
6.解:四边形是矩形,
,,
,
,
,
,
矩形的面积,
故选:.
7.解:相邻边长为,的矩形的周长为12,面积为6,
,,
则
.
故选:.
8.解:四边形是矩形,
,,,
,
垂直平分,
,
,
,
,
;
故选:.
9.解:,,
,
四边形是矩形,
,,,
,
,
,
,
,
,
故选:.
10.解:四边形是矩形,
,,,,
平分,
,
,
,
,故①正确;
,
,
故②正确;
四边形是矩形,
,
点为的中点,
,,
,
在和中,
,
.
,,
,
是等腰直角三角形,
,
,
,故③正确;
过点作于,
,
设,,
,,
,是等腰直角三角形,
,,
,,
;故④错误;
故选:.
二.填空题(共6小题)
11.解:若使平行四边形变为矩形,可添加的条件是:
;(对角线相等的平行四边形是矩形)
.(有一个角是直角的平行四边形是矩形)
故答案为:或.
12.解:①两组对边分别相等的四边形为平行四边形.
②一组对边平行且相等的四边形是平行四边形,一个角是直角的平行四边形是矩形.
③易证:
,
一组对边平行且相等的四边形是平行四边形,
一个角是直角或对角线相等的平行四边形是矩形.
④易证:,
,
两组对边分别相等的四边形是平行四边形,
一个角是直角的平行四边形是矩形,
故答案为②③④.
13.解:设,,
矩形周长为,
,
,
对角线的长是,
,
,
,
,
矩形面积为.
故答案为:.
14.解:在中,,
矩形中,,,
点、分别是、的中点,
是的中位线,
,
故答案为:5.
15.解:四边形是矩形,
,
,
平分,
,
,
,
在直角中,,
.
故答案为1.
16.解:如图,过点作于,
四边形是矩形,
,,,,
,,
在和中,
,
,
,
,,
,,
,,
,
,
,,
,
矩形的面积,
故答案为:.
三.解答题(共5小题)
17.证明:四边形是平行四边形,
,
,,
四边形是平行四边形,
,
,
四边形是矩形.
18.(1)证明:在四边形中,,
,
,,
,
即,
,
四边形是平行四边形.
(2)解:当时,四边形是矩形,
理由:,,,
,
.
.
四边形是平行四边形,
四边形是矩形.
19.证明:(1)在平行四边形中,,,,则.
又,
,
四边形为平行四边形,
.
在与中,
,
;
(2)由(1)知,四边形为平行四边形,则,.
四边形为平行四边形,
,即.
又,,
,
,
,即,
平行四边形为矩形.
20.(1)证明:四边形是平行四边形,
即,
,
点是的中点,
,
在和中,
,
;
(2)解:四边形是矩形,
,,,
,
,
,
,
四边形是平行四边形,
.
21.解:(1)如图2,连接,
,,
,
点关于直线的对称点,
,,,
,
,
;
(2)如图3,当点在线段上时,
点关于直线的对称点,
,,,
,
,
,
,
;
如图4,当点在线段的延长线上时,
点关于直线的对称点,
,,,
,
,
,
,
,
综上所述:或15.
