苏科版七年级数学下册 9.4 乘法公式 教案
文档属性
| 名称 | 苏科版七年级数学下册 9.4 乘法公式 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 76.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 00:00:00 | ||
图片预览

文档简介
乘法公式
【教学目标】
1.会推导平方差公式,并能运用公式进行简单的计算。
2.通过图形面积,感受乘法公式的直观理解。
3.经历探索平方差公式的过程,发展有符号感和推理能力。
【教学重点】
能正确地运用公式进行简单计算。
【教学难点】
正确理解运用公式并进行计算。
【教学过程】
一、回顾复习:
1.完全平方公式:
2.计算:
(1) (2) (3)
3.计算:
(1)(3x+y)(3x-y) (2)(3+5a)(3-5a) (3)20112-2010×2012
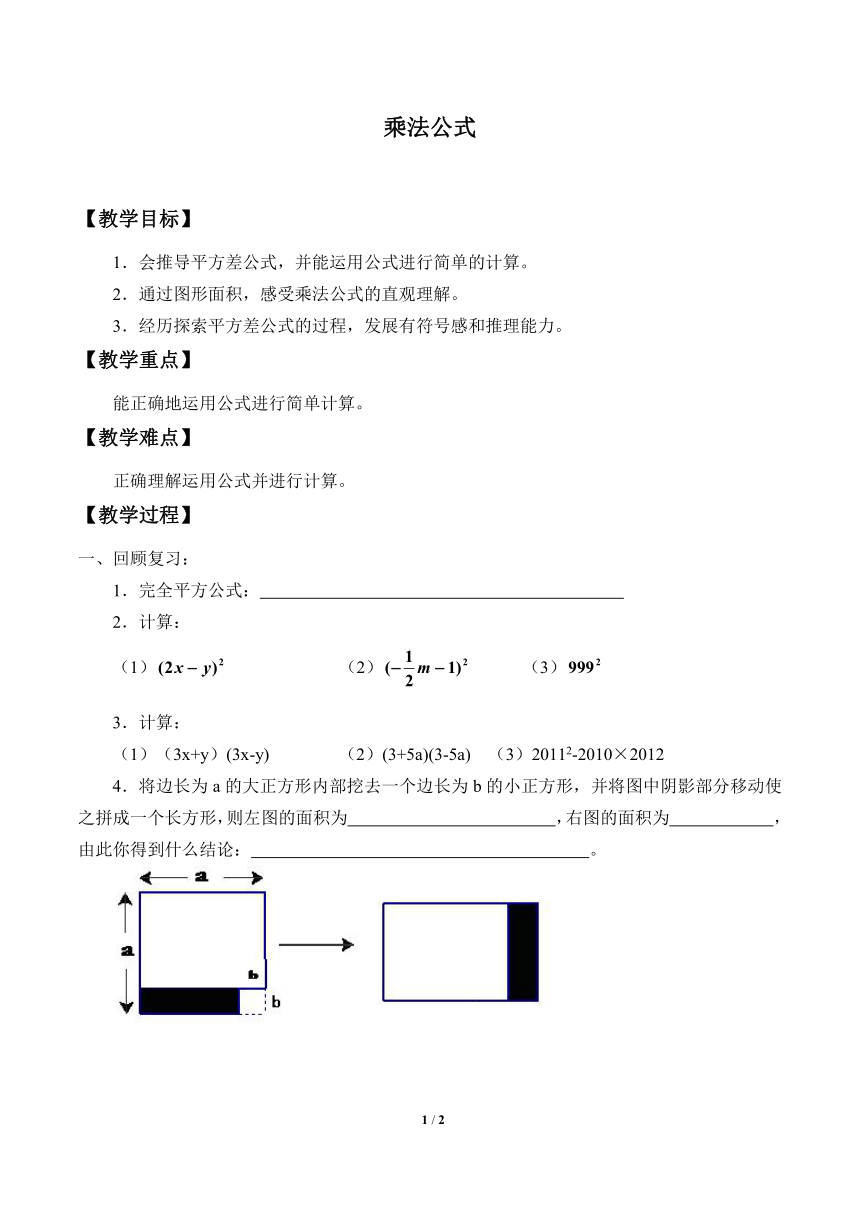
4.将边长为a的大正方形内部挖去一个边长为b的小正方形,并将图中阴影部分移动使之拼成一个长方形,则左图的面积为 ,右图的面积为 ,由此你得到什么结论: 。
二、新课学习:
(一)公式的推导及特征
由“回顾复习4”你得到什么结论,你能用多项式乘法运算法则验证吗?
小结:
1.公式的名称
2.公式的特点
(二)公式的运用
例1.计算
(1)(5x+y)(5x-y) (2)(-x+3y)(-x-3y)
(3)(m+2n)(2n-m) (4)(x-2y)(-x-2y)
(5)(3a+4b)(4a-3b) (6)(x+2y)(-x-2y))
例2.计算
(1)49×51 (2)20112-2010×2012
三、拓展延伸:
(1)
(2)(a+2)(a-2)-(a-1)(a+5)
(3)
1 / 1
【教学目标】
1.会推导平方差公式,并能运用公式进行简单的计算。
2.通过图形面积,感受乘法公式的直观理解。
3.经历探索平方差公式的过程,发展有符号感和推理能力。
【教学重点】
能正确地运用公式进行简单计算。
【教学难点】
正确理解运用公式并进行计算。
【教学过程】
一、回顾复习:
1.完全平方公式:
2.计算:
(1) (2) (3)
3.计算:
(1)(3x+y)(3x-y) (2)(3+5a)(3-5a) (3)20112-2010×2012
4.将边长为a的大正方形内部挖去一个边长为b的小正方形,并将图中阴影部分移动使之拼成一个长方形,则左图的面积为 ,右图的面积为 ,由此你得到什么结论: 。
二、新课学习:
(一)公式的推导及特征
由“回顾复习4”你得到什么结论,你能用多项式乘法运算法则验证吗?
小结:
1.公式的名称
2.公式的特点
(二)公式的运用
例1.计算
(1)(5x+y)(5x-y) (2)(-x+3y)(-x-3y)
(3)(m+2n)(2n-m) (4)(x-2y)(-x-2y)
(5)(3a+4b)(4a-3b) (6)(x+2y)(-x-2y))
例2.计算
(1)49×51 (2)20112-2010×2012
三、拓展延伸:
(1)
(2)(a+2)(a-2)-(a-1)(a+5)
(3)
1 / 1
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
