浙江省江山市实验中学2012-2013学年高二12月月考数学(文)试题
文档属性
| 名称 | 浙江省江山市实验中学2012-2013学年高二12月月考数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 140.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-11 00:00:00 | ||
图片预览


文档简介
江山市实验中学2012-2013学年高二12月月考数学(文)试题
注意事项: 1. 本卷考试时间为120分钟,满分为150分;
2. 本卷分试题卷和答题卷两部分,请考生一律在答题卷上答题。
参考公式:棱柱的体积公式 其中表示棱柱的底面积,表示棱柱的高 棱锥的体积公式 其中表示棱锥的底面积,表示棱锥的高
棱台的体积公式 其中S1、S2分别表示棱台的上、下底面积,表示棱台的高
球的表面积公式
球的体积公式 其中表示球的半径
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知过点P(—2,m),Q(m,4)的直线的倾斜角为45°,则m的值为( )
A.1 B.2 C.3 D.4
2.设,则线段AB的中点在空间直角坐标系中的位置是 ( )
A.在轴上 B.在面内 C.在面内 D.在面内
3. 设、是两条不同的直线,、是两个不同的平面.考查下列命题,其中正确的命题是
A、 B、
C、 D、
4.把边长为a的正方形卷成圆柱形,则圆柱的体积是( )
A B C D
5.如图:已知△ABC是直角三角形,∠ACB=90°M为AB的中点,
PM⊥△ABC所在的
平面,那么PA、PB、PC的大小关系是( )
A.PA>PB>PC B.PB>PA>PC
C.PC>PA>PB D.PA=PB=PC
6.将长方体截去一个四棱锥,得到的几何体如右图所示,则该几何体的左视图为( )
7. 已知圆:+=1,圆与圆关于直线对称,则圆的方程( )
A.+=1 B. +=1
C.+=1 D.+=1
8.已知直线方程为和分别为直线上和外的点,则方程表示( )
A.过点且与垂直的直线 B.与重合的直线
C.过点且与平行的直线 D.不过点,但与平行的直线
9.已知直线恒过定点,若点在直线上,
则的最小值为( )
A.2 B. C.4 D.
10.如图,正方体ABCD-A1B1C1D1的棱长为1,点M是对角线A1B上的动点,则AM+MD1
的最小值为( )
(A) (B) (C) (D)2
二、填空题:本大题共7小题,每小题4分,共28分。
11过点P(2,1)与直线l:y=3x-4垂直的直线方程为___▲_;
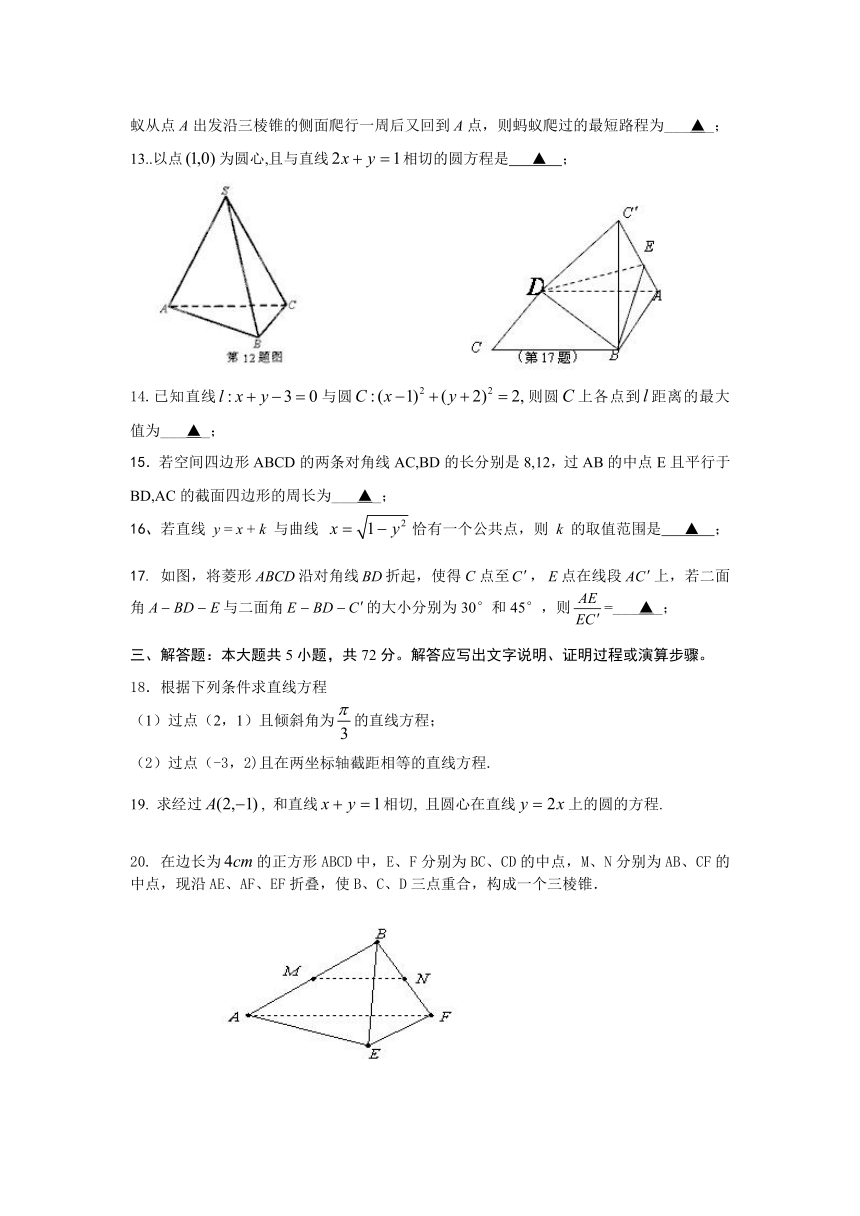
12.在三棱锥S—ABC中,SA=SB=SC=1,∠ASB=∠ASC=∠BSC=30°,如图,一只蚂蚁从点A出发沿三棱锥的侧面爬行一周后又回到A点,则蚂蚁爬过的最短路程为___▲_;
13..以点为圆心,且与直线相切的圆方程是 ▲ ;
14.已知直线与圆则圆上各点到距离的最大值为___▲_;
15.若空间四边形ABCD的两条对角线AC,BD的长分别是8,12,过AB的中点E且平行于BD,AC的截面四边形的周长为___▲_;
16、若直线 y = x + k 与曲线 恰有一个公共点,则 k 的取值范围是 ▲ ;
17. 如图,将菱形沿对角线折起,使得C点至,点在线段上,若二面角与二面角的大小分别为30°和45°,则=___▲_;
三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18.根据下列条件求直线方程
(1)过点(2,1)且倾斜角为的直线方程;
(2)过点(-3,2)且在两坐标轴截距相等的直线方程.
19. 求经过, 和直线相切, 且圆心在直线上的圆的方程.
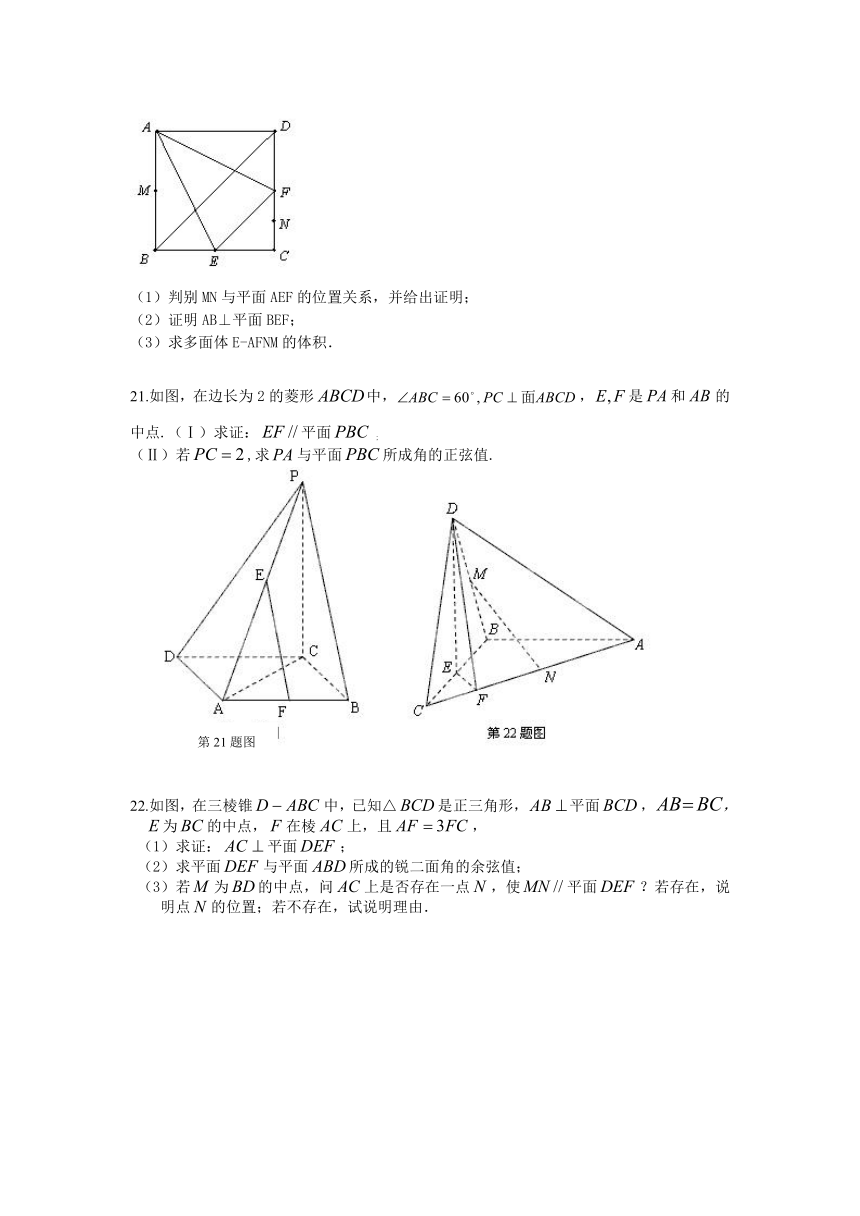
20. 在边长为的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
(1)判别MN与平面AEF的位置关系,并给出证明;
(2)证明AB⊥平面BEF;
(3)求多面体E-AFNM的体积.
21.如图,在边长为2的菱形中,,是和的中点.(Ⅰ)求证:平面 ;
(Ⅱ)若,求与平面所成角的正弦值.
22.如图,在三棱锥中,已知△是正三角形,平面,,为的中点,在棱上,且,
(1)求证:平面;
(2)求平面与平面所成的锐二面角的余弦值;
(3)若为的中点,问上是否存在一点,使平面?若存在,说明点的位置;若不存在,试说明理由.
2012学年高二年级数学文科参考答案及评分细则
一、选择题:本大题共10小题,每小题5分,共50分。
题号
1
2
3
4
5
6
7
8
9
10
答案
A
C
B
C
D
C
B
C
C
A
二、填空题:本大题共7小题,每小题4分,共28分。
20. (本小题满分14分)【答案】(1),证明见解析(2)证明见解析(3)
【解析】(I)显然可判断出MN//AF,所以MN//平面AEF.
(2)由平面图形可知,即立体图形中,问题得证.
(3)可利用来求体积.
解:, ………1分
证明如下:
因翻折后B、C、D重合(如图),
所以MN应是的一条中位线,…………3分
则.………6分
…………………14分
22.(本小题满分15分)
解一:(1)取AC的中点H,因为 AB=BC,所以 BH⊥AC.
因为 AF=3FC,所以 F为CH的中点.
因为 E为BC的中点,所以 EF∥BH.则EF⊥AC.
因为 △BCD是正三角形,所以 DE⊥BC.
因为 AB⊥平面BCD,所以 AB⊥DE.
因为 AB∩BC=B,所以 DE⊥平面ABC.所以 DE⊥AC.
因为 DE∩EF=E,所以 AC⊥平面DEF
(2)
(3)存在这样的点N,
当CN=时,MN∥平面DEF.
连CM,设CM∩DE=O,连OF.
由条件知,O为△BCD的重心,CO=CM.
所以 当CF=CN时,MN∥OF.所以 CN=
解二:建立直角坐标系
注意事项: 1. 本卷考试时间为120分钟,满分为150分;
2. 本卷分试题卷和答题卷两部分,请考生一律在答题卷上答题。
参考公式:棱柱的体积公式 其中表示棱柱的底面积,表示棱柱的高 棱锥的体积公式 其中表示棱锥的底面积,表示棱锥的高
棱台的体积公式 其中S1、S2分别表示棱台的上、下底面积,表示棱台的高
球的表面积公式
球的体积公式 其中表示球的半径
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知过点P(—2,m),Q(m,4)的直线的倾斜角为45°,则m的值为( )
A.1 B.2 C.3 D.4
2.设,则线段AB的中点在空间直角坐标系中的位置是 ( )
A.在轴上 B.在面内 C.在面内 D.在面内
3. 设、是两条不同的直线,、是两个不同的平面.考查下列命题,其中正确的命题是
A、 B、
C、 D、
4.把边长为a的正方形卷成圆柱形,则圆柱的体积是( )
A B C D
5.如图:已知△ABC是直角三角形,∠ACB=90°M为AB的中点,
PM⊥△ABC所在的
平面,那么PA、PB、PC的大小关系是( )
A.PA>PB>PC B.PB>PA>PC
C.PC>PA>PB D.PA=PB=PC
6.将长方体截去一个四棱锥,得到的几何体如右图所示,则该几何体的左视图为( )
7. 已知圆:+=1,圆与圆关于直线对称,则圆的方程( )
A.+=1 B. +=1
C.+=1 D.+=1
8.已知直线方程为和分别为直线上和外的点,则方程表示( )
A.过点且与垂直的直线 B.与重合的直线
C.过点且与平行的直线 D.不过点,但与平行的直线
9.已知直线恒过定点,若点在直线上,
则的最小值为( )
A.2 B. C.4 D.
10.如图,正方体ABCD-A1B1C1D1的棱长为1,点M是对角线A1B上的动点,则AM+MD1
的最小值为( )
(A) (B) (C) (D)2
二、填空题:本大题共7小题,每小题4分,共28分。
11过点P(2,1)与直线l:y=3x-4垂直的直线方程为___▲_;
12.在三棱锥S—ABC中,SA=SB=SC=1,∠ASB=∠ASC=∠BSC=30°,如图,一只蚂蚁从点A出发沿三棱锥的侧面爬行一周后又回到A点,则蚂蚁爬过的最短路程为___▲_;
13..以点为圆心,且与直线相切的圆方程是 ▲ ;
14.已知直线与圆则圆上各点到距离的最大值为___▲_;
15.若空间四边形ABCD的两条对角线AC,BD的长分别是8,12,过AB的中点E且平行于BD,AC的截面四边形的周长为___▲_;
16、若直线 y = x + k 与曲线 恰有一个公共点,则 k 的取值范围是 ▲ ;
17. 如图,将菱形沿对角线折起,使得C点至,点在线段上,若二面角与二面角的大小分别为30°和45°,则=___▲_;
三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18.根据下列条件求直线方程
(1)过点(2,1)且倾斜角为的直线方程;
(2)过点(-3,2)且在两坐标轴截距相等的直线方程.
19. 求经过, 和直线相切, 且圆心在直线上的圆的方程.
20. 在边长为的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
(1)判别MN与平面AEF的位置关系,并给出证明;
(2)证明AB⊥平面BEF;
(3)求多面体E-AFNM的体积.
21.如图,在边长为2的菱形中,,是和的中点.(Ⅰ)求证:平面 ;
(Ⅱ)若,求与平面所成角的正弦值.
22.如图,在三棱锥中,已知△是正三角形,平面,,为的中点,在棱上,且,
(1)求证:平面;
(2)求平面与平面所成的锐二面角的余弦值;
(3)若为的中点,问上是否存在一点,使平面?若存在,说明点的位置;若不存在,试说明理由.
2012学年高二年级数学文科参考答案及评分细则
一、选择题:本大题共10小题,每小题5分,共50分。
题号
1
2
3
4
5
6
7
8
9
10
答案
A
C
B
C
D
C
B
C
C
A
二、填空题:本大题共7小题,每小题4分,共28分。
20. (本小题满分14分)【答案】(1),证明见解析(2)证明见解析(3)
【解析】(I)显然可判断出MN//AF,所以MN//平面AEF.
(2)由平面图形可知,即立体图形中,问题得证.
(3)可利用来求体积.
解:, ………1分
证明如下:
因翻折后B、C、D重合(如图),
所以MN应是的一条中位线,…………3分
则.………6分
…………………14分
22.(本小题满分15分)
解一:(1)取AC的中点H,因为 AB=BC,所以 BH⊥AC.
因为 AF=3FC,所以 F为CH的中点.
因为 E为BC的中点,所以 EF∥BH.则EF⊥AC.
因为 △BCD是正三角形,所以 DE⊥BC.
因为 AB⊥平面BCD,所以 AB⊥DE.
因为 AB∩BC=B,所以 DE⊥平面ABC.所以 DE⊥AC.
因为 DE∩EF=E,所以 AC⊥平面DEF
(2)
(3)存在这样的点N,
当CN=时,MN∥平面DEF.
连CM,设CM∩DE=O,连OF.
由条件知,O为△BCD的重心,CO=CM.
所以 当CF=CN时,MN∥OF.所以 CN=
解二:建立直角坐标系
同课章节目录
