青岛版八年级数学上册2.4线段的垂直平分线 课件(共22张PPT)
文档属性
| 名称 | 青岛版八年级数学上册2.4线段的垂直平分线 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
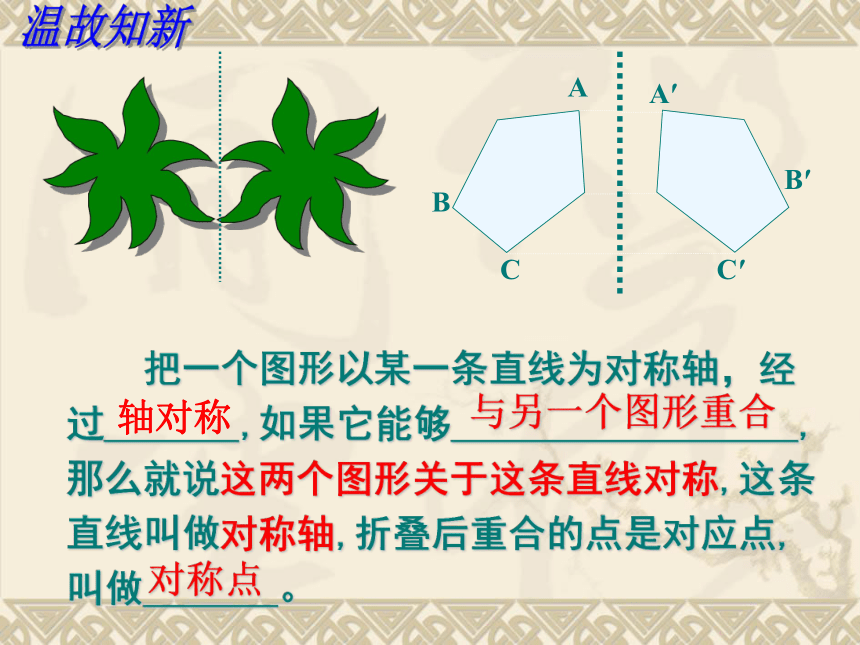
把一个图形以某一条直线为对称轴,经过 ,如果它能够 ,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做 。
A′
A
B
C
B′
C′
与另一个图形重合
对称点
轴对称
一个图形的一部分以某一条直线为 ,经过轴对称两侧的图形能够 ,这个图形就是轴对称图形。
折痕所在的这条直线叫做______。
对称轴
完全重合
对称轴
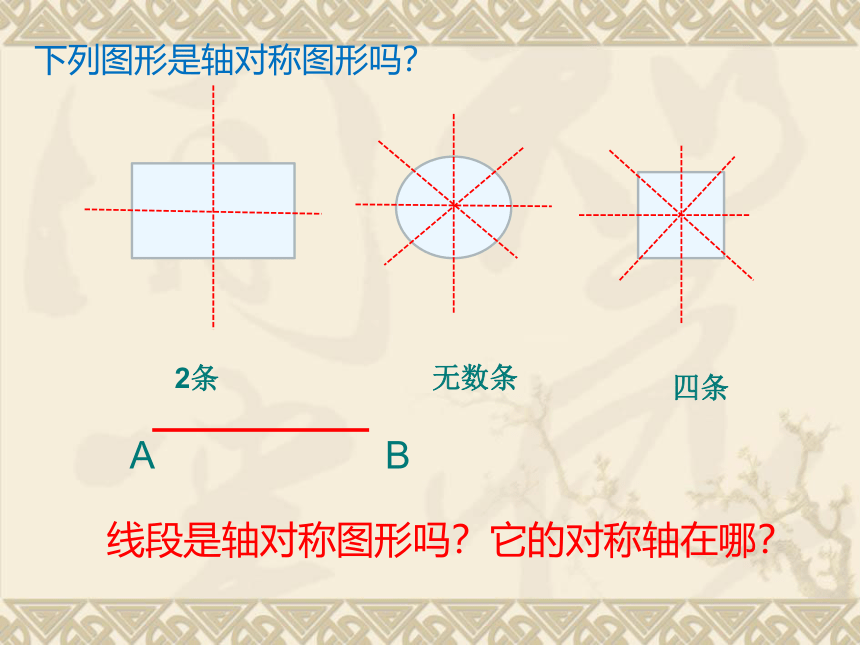
2条
无数条
四条
A
B
线段是轴对称图形吗?它的对称轴在哪?
下列图形是轴对称图形吗?
自学指导:自学课本P45----P47页,小组完成下列问题
1.线段是轴对称图形吗?线段垂直平分线的定义是什么?能用数学符号语言描述线段垂直平分线的定义吗?
2.线段垂直平分线的性质是什么?在性质的探究(2)中,对于垂直平分线上的任意一点P分了哪两种情况?你能用几何证明的方法来说明吗?
3.到线段两端距离相等的点一定在线段的垂直平分线上吗?也需要分类探究吗?请你说明一下。
4.如何用尺规做出已知线段的垂直平分线?明确作图方法及步骤;在作图过程中,为什么必须以大于 1/2 AB的长为半径画弧呢?
线段垂直平分线:垂直并且平分一条线段的直线叫做这条线段的垂直平分线
A
B
M
N
O
符号语言:
∵MN⊥AB 垂足为O
且AO=BO
∴直线MN是线段AB的垂直平分线
反过来:
∵直线MN是线段AB的垂直平分线
∴MN⊥AB,AO=BO
即:∠AOM= ∠BOM=90
AO=BO
线段垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等。
A
B
M
N
P
已知:线段AB,直线MN是线段AB的垂直平分线
交点为O,P为MN上任意一点
求证:PA=PB
证明:(1)当P点在AB上时
∵MN是线段AB的垂直平分线
∴P为线段AB的中点
∴PA=PB
(2)当P点不在AB上时
连接PA,PB
∵MN为线段AB的垂直平分线
∴∠AOP= ∠BOP=90 ,AO=BO
在△AOP与△BOP中
AO=BO
∠AOP= ∠BOP
OP=OP
A
B
M
N
P
O
∴ △AOP ≌ △BOP(SAS)
∴ PA=PB
基础闯关
1.如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED= cm;如果∠ECD=600,那么∠EDC= 0.
E
D
A
B
C
7
60
2.p47页,练习第一题
到线段两端距离相等的点在线段的垂直平分线上
互逆关系
A
B
已知:线段AB和任意一点P,满足PA=PB
求证:P点在线段的垂直平分线上
P
证明:(1)当P在线段AB上时
∵PA=PB
∴P为线段AB的中点
∴点P在线段AB的垂直平分线上
(2)当点P不在AB上时
取AB的中点O,连接PO
∵O为AB的中点
∴AO=BO
在△AOP与△BOP中
AO=BO
OP=OP
PA=PB
∴ △AOP ≌ △BOP(SSS)
A
B
P
O
∴ ∠AOP= ∠ BOP
∵ ∠AOP+ ∠ BOP=180
∴ ∠AOP=∠ BOP=90
∴PO是线段AB的垂直平分线
即P在线段AB的垂直平分线上
1. 已知:△ABC的边AB,AC的垂直平分线相交于点P.如图
求证:点P在BC的垂直平分线上
B
C
A
P
证明:连接PA,PB,PC.
∵点P在AB,AC的垂直平分线上 (已知)
∴PA=PB,PA=PC
(线段垂直平分线上的点与线段两端距离相等)
∴PB=PC(等量代换)
∴点P在BC的垂直平分线上.
(与线段两端距离相等的点在这条线段的垂直平分线上)
应用
1、如图, NM是线段AB的中垂线,
下列说法正确的有: 。
①AB⊥MN,②AD=DB, ③MN⊥AB, ④MD=DN,⑤AB是MN的垂直平分线
A
B
M
N
D
①②③
2、下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上的点;④若EA=EB,则过点E的直线垂直平分线段AB.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
C
线段垂直平分线的画法
<一>操作:画线段垂直平分线
尺规画法
①分别以点A、B为圆心,大于 AB长为半径画弧交于点E、F②过点E、F作直线. 则直线EF就是线段AB的垂直平分线(如图)
<二>想一想
1、作法中为什么要“大于 AB长为半径”呢?
2、为什么这样作出的直线就是线段AB的垂直平分线呢?
A
B
E
F
O
作法中为什么要“大于 AB长为半径画弧”呢?
假若以A,B为圆心,
当小于 AB长为半径画弧时,则两弧无交点
当等于 AB长为半径画弧时,则两弧只有一个交点
而确定垂直平分线需要两点,故以上均不能作出线段的垂直平分线。
为什么这样作出的直线就是线段AB的垂直平分线呢?
分析:
要证EF是AB的垂直平分线即AO=BO,∠AOE=∠BOE=90°
△AOE≌ △BOE(SAS)
AE=BE(已作)
∠1= ∠2
OE=OE(公共边)
△AEF ≌ △BEF(sss)
AE=BE(已作)
AF=BF(已作)
EF=EF (公共边)
你能说出证明过程吗?
A
B
E
F
O
1
2
线段垂直平分线的应用
公路L同侧的A、B两村,共同出资在公路边修建一个农产品仓库C,使仓库到A,B两村距离相等.你如何确定仓库C的位置?
A
B
L
C
1.线段垂直平分线的定义及性质
2.线段垂直平分线的性质的应用
3.线段垂直平分线的画法
如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长。
D
C
B
E
A
解:
∵ED是线段AB的垂直平分线
∴BD=AD
∵ △BCD的周长=BD+DC+BC
∴ △BCD的周长=AD+DC+BC
=AC+BC
=12+7=19
如图,在△ABC上,已知点D在BC上,且BD+AD=BC.求证: 点D在AC的垂直平分线上.
证明:
∵ BD+AD=BC
∴AD=BC-BD=CD
∴点D在AC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
布置作业:
课本习题2.4,3,4,5
把一个图形以某一条直线为对称轴,经过 ,如果它能够 ,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做 。
A′
A
B
C
B′
C′
与另一个图形重合
对称点
轴对称
一个图形的一部分以某一条直线为 ,经过轴对称两侧的图形能够 ,这个图形就是轴对称图形。
折痕所在的这条直线叫做______。
对称轴
完全重合
对称轴
2条
无数条
四条
A
B
线段是轴对称图形吗?它的对称轴在哪?
下列图形是轴对称图形吗?
自学指导:自学课本P45----P47页,小组完成下列问题
1.线段是轴对称图形吗?线段垂直平分线的定义是什么?能用数学符号语言描述线段垂直平分线的定义吗?
2.线段垂直平分线的性质是什么?在性质的探究(2)中,对于垂直平分线上的任意一点P分了哪两种情况?你能用几何证明的方法来说明吗?
3.到线段两端距离相等的点一定在线段的垂直平分线上吗?也需要分类探究吗?请你说明一下。
4.如何用尺规做出已知线段的垂直平分线?明确作图方法及步骤;在作图过程中,为什么必须以大于 1/2 AB的长为半径画弧呢?
线段垂直平分线:垂直并且平分一条线段的直线叫做这条线段的垂直平分线
A
B
M
N
O
符号语言:
∵MN⊥AB 垂足为O
且AO=BO
∴直线MN是线段AB的垂直平分线
反过来:
∵直线MN是线段AB的垂直平分线
∴MN⊥AB,AO=BO
即:∠AOM= ∠BOM=90
AO=BO
线段垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等。
A
B
M
N
P
已知:线段AB,直线MN是线段AB的垂直平分线
交点为O,P为MN上任意一点
求证:PA=PB
证明:(1)当P点在AB上时
∵MN是线段AB的垂直平分线
∴P为线段AB的中点
∴PA=PB
(2)当P点不在AB上时
连接PA,PB
∵MN为线段AB的垂直平分线
∴∠AOP= ∠BOP=90 ,AO=BO
在△AOP与△BOP中
AO=BO
∠AOP= ∠BOP
OP=OP
A
B
M
N
P
O
∴ △AOP ≌ △BOP(SAS)
∴ PA=PB
基础闯关
1.如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED= cm;如果∠ECD=600,那么∠EDC= 0.
E
D
A
B
C
7
60
2.p47页,练习第一题
到线段两端距离相等的点在线段的垂直平分线上
互逆关系
A
B
已知:线段AB和任意一点P,满足PA=PB
求证:P点在线段的垂直平分线上
P
证明:(1)当P在线段AB上时
∵PA=PB
∴P为线段AB的中点
∴点P在线段AB的垂直平分线上
(2)当点P不在AB上时
取AB的中点O,连接PO
∵O为AB的中点
∴AO=BO
在△AOP与△BOP中
AO=BO
OP=OP
PA=PB
∴ △AOP ≌ △BOP(SSS)
A
B
P
O
∴ ∠AOP= ∠ BOP
∵ ∠AOP+ ∠ BOP=180
∴ ∠AOP=∠ BOP=90
∴PO是线段AB的垂直平分线
即P在线段AB的垂直平分线上
1. 已知:△ABC的边AB,AC的垂直平分线相交于点P.如图
求证:点P在BC的垂直平分线上
B
C
A
P
证明:连接PA,PB,PC.
∵点P在AB,AC的垂直平分线上 (已知)
∴PA=PB,PA=PC
(线段垂直平分线上的点与线段两端距离相等)
∴PB=PC(等量代换)
∴点P在BC的垂直平分线上.
(与线段两端距离相等的点在这条线段的垂直平分线上)
应用
1、如图, NM是线段AB的中垂线,
下列说法正确的有: 。
①AB⊥MN,②AD=DB, ③MN⊥AB, ④MD=DN,⑤AB是MN的垂直平分线
A
B
M
N
D
①②③
2、下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上的点;④若EA=EB,则过点E的直线垂直平分线段AB.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
C
线段垂直平分线的画法
<一>操作:画线段垂直平分线
尺规画法
①分别以点A、B为圆心,大于 AB长为半径画弧交于点E、F②过点E、F作直线. 则直线EF就是线段AB的垂直平分线(如图)
<二>想一想
1、作法中为什么要“大于 AB长为半径”呢?
2、为什么这样作出的直线就是线段AB的垂直平分线呢?
A
B
E
F
O
作法中为什么要“大于 AB长为半径画弧”呢?
假若以A,B为圆心,
当小于 AB长为半径画弧时,则两弧无交点
当等于 AB长为半径画弧时,则两弧只有一个交点
而确定垂直平分线需要两点,故以上均不能作出线段的垂直平分线。
为什么这样作出的直线就是线段AB的垂直平分线呢?
分析:
要证EF是AB的垂直平分线即AO=BO,∠AOE=∠BOE=90°
△AOE≌ △BOE(SAS)
AE=BE(已作)
∠1= ∠2
OE=OE(公共边)
△AEF ≌ △BEF(sss)
AE=BE(已作)
AF=BF(已作)
EF=EF (公共边)
你能说出证明过程吗?
A
B
E
F
O
1
2
线段垂直平分线的应用
公路L同侧的A、B两村,共同出资在公路边修建一个农产品仓库C,使仓库到A,B两村距离相等.你如何确定仓库C的位置?
A
B
L
C
1.线段垂直平分线的定义及性质
2.线段垂直平分线的性质的应用
3.线段垂直平分线的画法
如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长。
D
C
B
E
A
解:
∵ED是线段AB的垂直平分线
∴BD=AD
∵ △BCD的周长=BD+DC+BC
∴ △BCD的周长=AD+DC+BC
=AC+BC
=12+7=19
如图,在△ABC上,已知点D在BC上,且BD+AD=BC.求证: 点D在AC的垂直平分线上.
证明:
∵ BD+AD=BC
∴AD=BC-BD=CD
∴点D在AC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
布置作业:
课本习题2.4,3,4,5
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
