人教版八年级数学 下册 第十八章18.1.1 平行四边形的性质第1课时 同步练习(word版含答案)
文档属性
| 名称 | 人教版八年级数学 下册 第十八章18.1.1 平行四边形的性质第1课时 同步练习(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 65.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 00:00:00 | ||
图片预览

文档简介
初中数学·人教版·八年级下册——第十八章 平行四边形
18.1 平行四边形
18.1.1 平行四边形的性质
第1课时 平行四边形的性质(1)
测试时间:20分钟
一、选择题
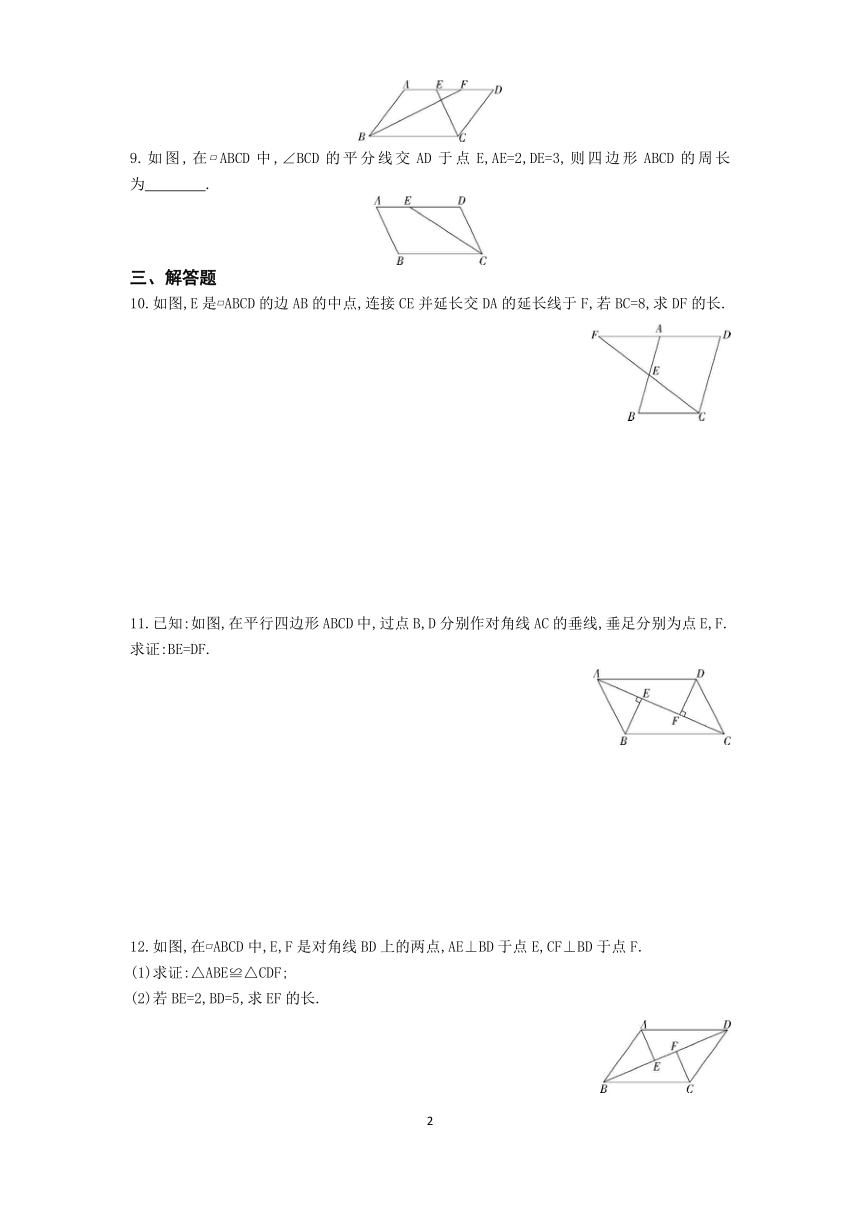
1.如图,在平行四边形ABCD中,∠A+∠C=130°,则∠B的度数为( )
A.130° B.115° C.105° D.95°
2.如图,在 ABCD中,AD=7,AB=5,DE平分∠ADC交BC于点E,则BE的长是( )
A.2 B.3 C.4 D.5
3.如图,在 ABCD中,AC=5 cm.若△ACD的周长为14 cm,则 ABCD的周长为( )
A.18 cm B.19 cm C.28 cm D.38 cm
4.(2020陕西延安富县期末)如图,在 ABCD中,CE⊥AB于点E.若∠BCE=28°,则∠D的度数是( )
A.28° B.38° C.52° D.62°
二、填空题
5.在平行四边形ABCD中,若∠A=38°,则∠C= .
6.如图,点E在 ABCD的边BC的延长线上,若∠DCE=60°,则∠A= °.
7.如图,在 ABCD中,若∠A=2∠B,则∠D= °.
8.如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=7,EF=1,则BC的长为 .
9.如图,在 ABCD中,∠BCD的平分线交AD于点E,AE=2,DE=3,则四边形ABCD的周长为 .
三、解答题
10.如图,E是 ABCD的边AB的中点,连接CE并延长交DA的延长线于F,若BC=8,求DF的长.
11.已知:如图,在平行四边形ABCD中,过点B,D分别作对角线AC的垂线,垂足分别为点E,F.求证:BE=DF.
12.如图,在 ABCD中,E,F是对角线BD上的两点,AE⊥BD于点E,CF⊥BD于点F.
(1)求证:△ABE≌△CDF;
(2)若BE=2,BD=5,求EF的长.
初中数学·人教版·八年级下册——第十八章 平行四边形
18.1 平行四边形
18.1.1 平行四边形的性质
第1课时 平行四边形的性质(1)
测试时间:20分钟
一、选择题
1.答案 B ∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,∴∠B+∠C=180°,
∵∠A+∠C=130°,∴∠C=65°,
∴∠B=180°-∠C=115°,故选B.
2.答案 A ∵四边形ABCD是平行四边形,
∴BC=AD=7,CD=AB=5,AD∥BC,∴∠ADE=∠DEC,
∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠CDE=∠DEC,∴EC=CD=5,
∴BE=BC-EC=2.故选A.
3.答案 A ∵△ACD的周长为14 cm,即AD+CD+AC=14 cm,且AC=5 cm,
∴AD+CD=9 cm,
∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,
∴ ABCD的周长为AB+BC+AD+CD=9+9=18(cm).
故选A.
4.答案 D ∵CE⊥AB,∴∠CEB=90°,∵∠BCE=28°,∴∠B=62°,
∵四边形ABCD是平行四边形,∴∠D=∠B=62°,故选D.
二、填空题
5.答案 38°
解析 ∵四边形ABCD是平行四边形,∴∠A=∠C,
∵∠A=38°,∴∠C=38°.
6.答案 120
解析 ∵∠DCE=60°,∴∠BCD=180°-60°=120°,
∵四边形ABCD是平行四边形,∴∠A=∠BCD=120°.
7.答案 60
解析 ∵四边形ABCD是平行四边形,∴∠A+∠B=180°,∠B=∠D,
∵∠A=2∠B,∴3∠B=180°,∴∠B=∠D=60°.
8.答案 13
解析 ∵四边形ABCD是平行四边形,
∴CD=AB=7,BC=AD,AD∥BC,
∵BF平分∠ABC,交AD于F,CE平分∠BCD,交AD于E,
∴∠ABF=∠CBF=∠AFB,∠BCE=∠DCE=∠CED,
∴AF=AB=7,DE=DC=7,
∴EF=AF+DE-AD=7+7-AD=1,
∴AD=13,∴BC=13.
故答案为13.
9.答案 16
解析 在 ABCD中,AD∥BC,CE平分∠BCD交AD于点E,AB=DC,AD=BC,
∴∠DEC=∠ECB,∠DCE=∠BCE,
∴∠DEC=∠DCE,
∴DE=DC=AB,
∵AE=2,DE=3,
∴AD=AE+DE=2+3=5,CD=DE=3,
∴AD+DC=5+3=8,
∴四边形ABCD的周长为2×8=16.
故答案为16.
三、解答题
10.解析 ∵E是 ABCD的边AB的中点,∴AE=BE,
∵四边形ABCD是平行四边形,
∴AD=BC=8,AD∥CB,∴∠F=∠BCE,
在△AEF和△BEC中,∴△AEF≌△BEC(AAS),
∴AF=BC=8,∴DF=AD+AF=16.
11.证明 ∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∴∠DAF=∠BCE,
∵BE⊥AC,DF⊥AC,∴∠BEC=∠DFA,
在△BCE和△DAF中,∴△BCE≌△DAF(AAS),∴BE=DF.
12.解析 (1)证明:∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在 ABCD中,AB∥CD,AB=CD,
∴∠ABE=∠CDF,
在△ABE和△CDF中,∴△ABE≌△CDF(AAS).
(2)∵△ABE≌△CDF,∴BE=DF,
∵BE=2,∴DF=2,
∵EF=BD-BE-FD,
∴EF=5-2-2=1.
1
18.1 平行四边形
18.1.1 平行四边形的性质
第1课时 平行四边形的性质(1)
测试时间:20分钟
一、选择题
1.如图,在平行四边形ABCD中,∠A+∠C=130°,则∠B的度数为( )
A.130° B.115° C.105° D.95°
2.如图,在 ABCD中,AD=7,AB=5,DE平分∠ADC交BC于点E,则BE的长是( )
A.2 B.3 C.4 D.5
3.如图,在 ABCD中,AC=5 cm.若△ACD的周长为14 cm,则 ABCD的周长为( )
A.18 cm B.19 cm C.28 cm D.38 cm
4.(2020陕西延安富县期末)如图,在 ABCD中,CE⊥AB于点E.若∠BCE=28°,则∠D的度数是( )
A.28° B.38° C.52° D.62°
二、填空题
5.在平行四边形ABCD中,若∠A=38°,则∠C= .
6.如图,点E在 ABCD的边BC的延长线上,若∠DCE=60°,则∠A= °.
7.如图,在 ABCD中,若∠A=2∠B,则∠D= °.
8.如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=7,EF=1,则BC的长为 .
9.如图,在 ABCD中,∠BCD的平分线交AD于点E,AE=2,DE=3,则四边形ABCD的周长为 .
三、解答题
10.如图,E是 ABCD的边AB的中点,连接CE并延长交DA的延长线于F,若BC=8,求DF的长.
11.已知:如图,在平行四边形ABCD中,过点B,D分别作对角线AC的垂线,垂足分别为点E,F.求证:BE=DF.
12.如图,在 ABCD中,E,F是对角线BD上的两点,AE⊥BD于点E,CF⊥BD于点F.
(1)求证:△ABE≌△CDF;
(2)若BE=2,BD=5,求EF的长.
初中数学·人教版·八年级下册——第十八章 平行四边形
18.1 平行四边形
18.1.1 平行四边形的性质
第1课时 平行四边形的性质(1)
测试时间:20分钟
一、选择题
1.答案 B ∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,∴∠B+∠C=180°,
∵∠A+∠C=130°,∴∠C=65°,
∴∠B=180°-∠C=115°,故选B.
2.答案 A ∵四边形ABCD是平行四边形,
∴BC=AD=7,CD=AB=5,AD∥BC,∴∠ADE=∠DEC,
∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠CDE=∠DEC,∴EC=CD=5,
∴BE=BC-EC=2.故选A.
3.答案 A ∵△ACD的周长为14 cm,即AD+CD+AC=14 cm,且AC=5 cm,
∴AD+CD=9 cm,
∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,
∴ ABCD的周长为AB+BC+AD+CD=9+9=18(cm).
故选A.
4.答案 D ∵CE⊥AB,∴∠CEB=90°,∵∠BCE=28°,∴∠B=62°,
∵四边形ABCD是平行四边形,∴∠D=∠B=62°,故选D.
二、填空题
5.答案 38°
解析 ∵四边形ABCD是平行四边形,∴∠A=∠C,
∵∠A=38°,∴∠C=38°.
6.答案 120
解析 ∵∠DCE=60°,∴∠BCD=180°-60°=120°,
∵四边形ABCD是平行四边形,∴∠A=∠BCD=120°.
7.答案 60
解析 ∵四边形ABCD是平行四边形,∴∠A+∠B=180°,∠B=∠D,
∵∠A=2∠B,∴3∠B=180°,∴∠B=∠D=60°.
8.答案 13
解析 ∵四边形ABCD是平行四边形,
∴CD=AB=7,BC=AD,AD∥BC,
∵BF平分∠ABC,交AD于F,CE平分∠BCD,交AD于E,
∴∠ABF=∠CBF=∠AFB,∠BCE=∠DCE=∠CED,
∴AF=AB=7,DE=DC=7,
∴EF=AF+DE-AD=7+7-AD=1,
∴AD=13,∴BC=13.
故答案为13.
9.答案 16
解析 在 ABCD中,AD∥BC,CE平分∠BCD交AD于点E,AB=DC,AD=BC,
∴∠DEC=∠ECB,∠DCE=∠BCE,
∴∠DEC=∠DCE,
∴DE=DC=AB,
∵AE=2,DE=3,
∴AD=AE+DE=2+3=5,CD=DE=3,
∴AD+DC=5+3=8,
∴四边形ABCD的周长为2×8=16.
故答案为16.
三、解答题
10.解析 ∵E是 ABCD的边AB的中点,∴AE=BE,
∵四边形ABCD是平行四边形,
∴AD=BC=8,AD∥CB,∴∠F=∠BCE,
在△AEF和△BEC中,∴△AEF≌△BEC(AAS),
∴AF=BC=8,∴DF=AD+AF=16.
11.证明 ∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∴∠DAF=∠BCE,
∵BE⊥AC,DF⊥AC,∴∠BEC=∠DFA,
在△BCE和△DAF中,∴△BCE≌△DAF(AAS),∴BE=DF.
12.解析 (1)证明:∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在 ABCD中,AB∥CD,AB=CD,
∴∠ABE=∠CDF,
在△ABE和△CDF中,∴△ABE≌△CDF(AAS).
(2)∵△ABE≌△CDF,∴BE=DF,
∵BE=2,∴DF=2,
∵EF=BD-BE-FD,
∴EF=5-2-2=1.
1
