数学六年级上沪教版3.1《比和比例》复习课件
文档属性
| 名称 | 数学六年级上沪教版3.1《比和比例》复习课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 106.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-11 20:55:53 | ||
图片预览



文档简介
课件17张PPT。比和比例的整理与复习1米=( )分米=( )厘米 1千米=( )米 =( ) 厘米
0.3平方米=( )平方分米=( )平方厘米
3.02吨=( )吨( )千克=( )千克
0.375=( ):( )=( ) ﹪=12÷ ( )=
速度×时间=( )
工作总量÷工作时间=( )
出粉率= ×100﹪
单价×( )=总价课前训练10003033020203837.53224路程工作效率数量100000100103000激趣明标1:50000001.什么叫比?举例说明,各部分名称是什么?
2.什么叫做比的基本性质?举例说明.
3.什么叫做比例?举例说明,各部分名称.
4.什么叫做比例的基本性质?举例说明.
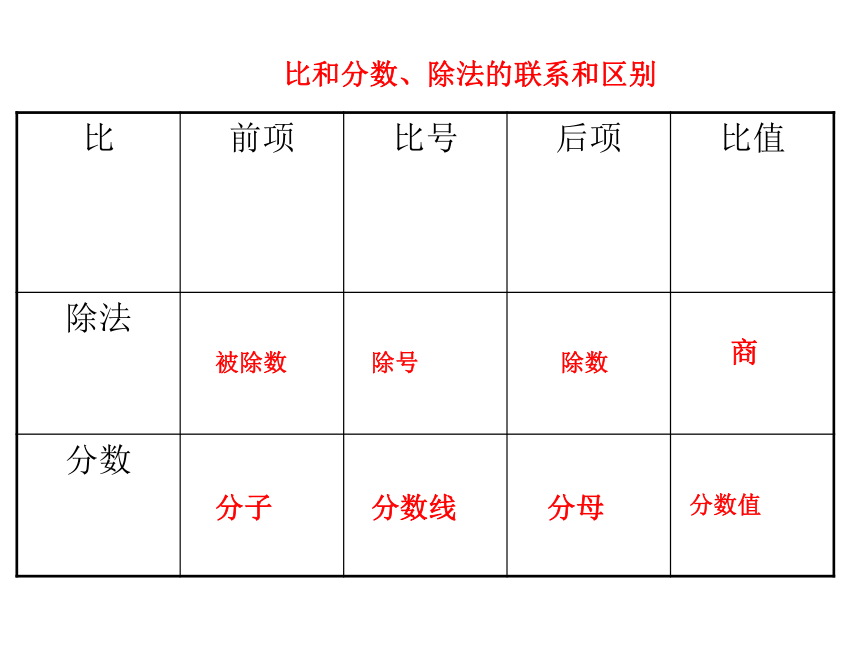
5.比和分数,除法的关系.
6.比.比例的基本性质的用处.
7.比例尺的意义及求比例尺应注意的事项.
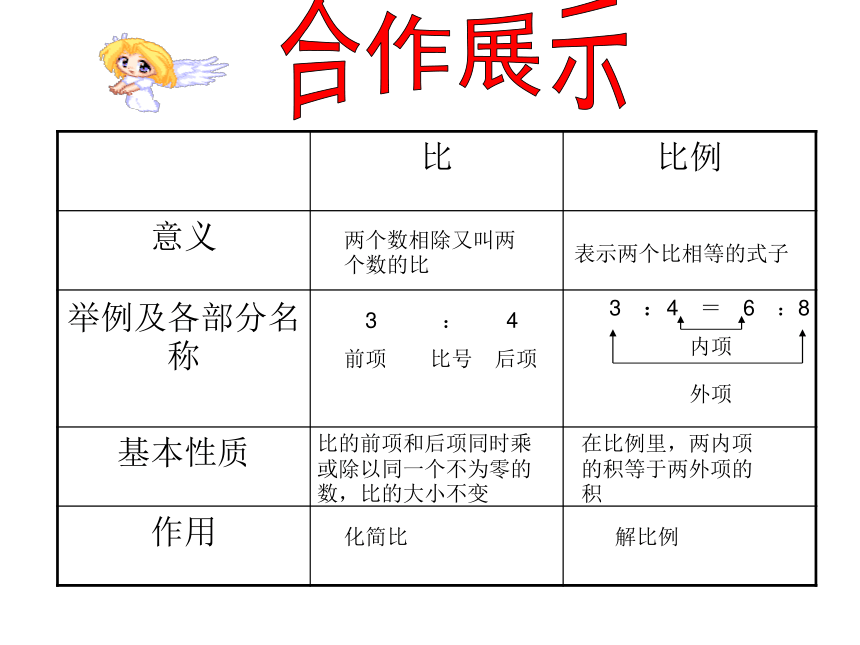
8.什么正比例?什么叫反比例?正反比例有什么联系与区别?自主学习合作展示表示两个比相等的式子
两个数相除又叫两个数的比 3 : 4
前项 比号 后项 3 :4 = 6 :8
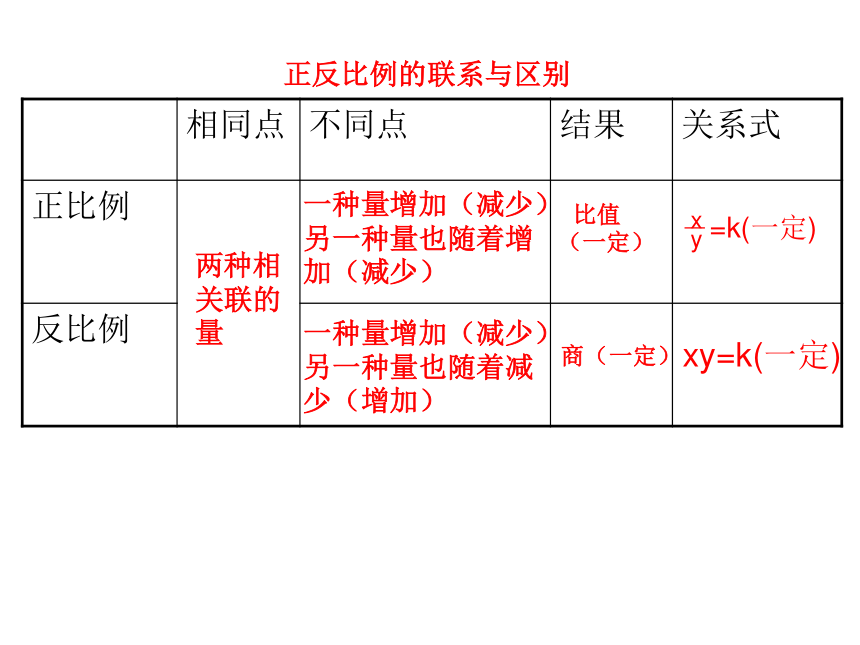
内项外项比的前项和后项同时乘或除以同一个不为零的数,比的大小不变在比例里,两内项的积等于两外项的积化简比解比例比和分数、除法的联系和区别被除数分子除号分数线除数分母商分数值正反比例的联系与区别两种相关联的量一种量增加(减少)另一种量也随着增加(减少)比值(一定)一种量增加(减少)另一种量也随着减少(增加)商(一定)xy=k(一定)比例尺比例尺的意义:比例尺的注意事项:在一幅图上,图上距离与实际距离的比,叫做这幅图的比例尺。
图上距离:实际距离=比例尺=比例尺或1.表示距离之间的比,不是面积之间的比。
2.比例尺表示两数之间的倍数关系,所以不能带单位。
3.比例尺的前项或后项通常写成1的形式。
4.运算时要注意统一单位。
一.填空题
.( ):( )=比例尺
4—小时:30分的比值是( )化简比是( )
比例尺分为( )和( )
( ):8=0.25=— =20÷( )
出粉率一定,面粉重量和小麦重量成( )比例.
被除数一定,除数和商成( )比例.
总价一定,单价和数量成( )比例.
小明每天看8页书,它看书的总页数和看书的天数成( )比例.
已知a×b=c( a.b.c 均不为0)
当a一定时,b和c成( )比例.当b一定时, a和c成( )比例4( )图上距离实际距离9数值比例尺9:1线段比例尺正反16反正802正正当堂测试当堂测试二.我是小判官
1.解比例就是解方程,则方程就是比例. ( )
2.300米:3千米化成最简整数比是100:1.( )
3. 因为A:B=4:3,所以3A=4B. ( )
4.一个比例的两个内项积是1,那么两个外项互为倒数.( )
5.把3克盐放入20克水中,盐占盐水的- . ( )
6.图上距离一定,比例尺和实际距离成反比例. ( )
7.正方形的面积和边长成反比例. ( )
8.有一幅图的比例尺是 米 ( )320√×√××√××解比例0.4:x=1.2:2 =解:1.2 =0.4×2
1.2 =0.8
=0.8÷1.2
= 解: =
=2一种微型零件的长是5毫米,画在图纸上长20厘米,求这幅图的比例尺是多少? 图上距离:实际距离
=20厘米:5毫米
=200毫米:5毫米
=40:1
答:这幅图的比例尺是40:1解决实际问题 用比例的方法解题。
1、一辆客车和一辆小汽车的速度比是1:2,如果小汽车的速度是120千米,那么客车的速度是多少千米?
2、花园小区1号楼的实际高度是45米,它的高度与模型高度的比是500:1。模型的高度是多少厘米?
解:设客车的速度是 千米.
:120=1:2
=60
答:客车的速度是60千米/时.
解:设模型的高度是 厘米。
(45×100): =500:1
500 =4500
=9
答:模型的高度是9厘米。
3、用某洗洁精洗水果以1:1000稀释,现在有3000毫升的水,要加入多少毫升的洗洁精?
解:设要加入 毫升的洗洁精.
:3000=1:1000
1000 =3000
=3
答:要加入3毫升的洗洁精.
拓展练习解:设需要 分钟.
8:3= :6
=
=16
答:需要16分钟.1.一根木料锯了3段需要8分钟,如果锯6段需要几分钟?(用比例知识解答)解:设完成任务需要 天。
8×30=(36÷3)
= 240÷12
=20
答:需要20天.2.某公司为“神州”七号飞船加工一批零件,原计划每天加工8个,30天完成任务,实际3天做了36个,照这样的速度加工,完成任务需要多少天?(用正、反比例解答)工作效率×工作时间=工作总量(一定)=解:设完成任务需要
=
=
=20
工作效率(一定)提升小结通过这节课的整理与复习,你有什么收获?
0.3平方米=( )平方分米=( )平方厘米
3.02吨=( )吨( )千克=( )千克
0.375=( ):( )=( ) ﹪=12÷ ( )=
速度×时间=( )
工作总量÷工作时间=( )
出粉率= ×100﹪
单价×( )=总价课前训练10003033020203837.53224路程工作效率数量100000100103000激趣明标1:50000001.什么叫比?举例说明,各部分名称是什么?
2.什么叫做比的基本性质?举例说明.
3.什么叫做比例?举例说明,各部分名称.
4.什么叫做比例的基本性质?举例说明.
5.比和分数,除法的关系.
6.比.比例的基本性质的用处.
7.比例尺的意义及求比例尺应注意的事项.
8.什么正比例?什么叫反比例?正反比例有什么联系与区别?自主学习合作展示表示两个比相等的式子
两个数相除又叫两个数的比 3 : 4
前项 比号 后项 3 :4 = 6 :8
内项外项比的前项和后项同时乘或除以同一个不为零的数,比的大小不变在比例里,两内项的积等于两外项的积化简比解比例比和分数、除法的联系和区别被除数分子除号分数线除数分母商分数值正反比例的联系与区别两种相关联的量一种量增加(减少)另一种量也随着增加(减少)比值(一定)一种量增加(减少)另一种量也随着减少(增加)商(一定)xy=k(一定)比例尺比例尺的意义:比例尺的注意事项:在一幅图上,图上距离与实际距离的比,叫做这幅图的比例尺。
图上距离:实际距离=比例尺=比例尺或1.表示距离之间的比,不是面积之间的比。
2.比例尺表示两数之间的倍数关系,所以不能带单位。
3.比例尺的前项或后项通常写成1的形式。
4.运算时要注意统一单位。
一.填空题
.( ):( )=比例尺
4—小时:30分的比值是( )化简比是( )
比例尺分为( )和( )
( ):8=0.25=— =20÷( )
出粉率一定,面粉重量和小麦重量成( )比例.
被除数一定,除数和商成( )比例.
总价一定,单价和数量成( )比例.
小明每天看8页书,它看书的总页数和看书的天数成( )比例.
已知a×b=c( a.b.c 均不为0)
当a一定时,b和c成( )比例.当b一定时, a和c成( )比例4( )图上距离实际距离9数值比例尺9:1线段比例尺正反16反正802正正当堂测试当堂测试二.我是小判官
1.解比例就是解方程,则方程就是比例. ( )
2.300米:3千米化成最简整数比是100:1.( )
3. 因为A:B=4:3,所以3A=4B. ( )
4.一个比例的两个内项积是1,那么两个外项互为倒数.( )
5.把3克盐放入20克水中,盐占盐水的- . ( )
6.图上距离一定,比例尺和实际距离成反比例. ( )
7.正方形的面积和边长成反比例. ( )
8.有一幅图的比例尺是 米 ( )320√×√××√××解比例0.4:x=1.2:2 =解:1.2 =0.4×2
1.2 =0.8
=0.8÷1.2
= 解: =
=2一种微型零件的长是5毫米,画在图纸上长20厘米,求这幅图的比例尺是多少? 图上距离:实际距离
=20厘米:5毫米
=200毫米:5毫米
=40:1
答:这幅图的比例尺是40:1解决实际问题 用比例的方法解题。
1、一辆客车和一辆小汽车的速度比是1:2,如果小汽车的速度是120千米,那么客车的速度是多少千米?
2、花园小区1号楼的实际高度是45米,它的高度与模型高度的比是500:1。模型的高度是多少厘米?
解:设客车的速度是 千米.
:120=1:2
=60
答:客车的速度是60千米/时.
解:设模型的高度是 厘米。
(45×100): =500:1
500 =4500
=9
答:模型的高度是9厘米。
3、用某洗洁精洗水果以1:1000稀释,现在有3000毫升的水,要加入多少毫升的洗洁精?
解:设要加入 毫升的洗洁精.
:3000=1:1000
1000 =3000
=3
答:要加入3毫升的洗洁精.
拓展练习解:设需要 分钟.
8:3= :6
=
=16
答:需要16分钟.1.一根木料锯了3段需要8分钟,如果锯6段需要几分钟?(用比例知识解答)解:设完成任务需要 天。
8×30=(36÷3)
= 240÷12
=20
答:需要20天.2.某公司为“神州”七号飞船加工一批零件,原计划每天加工8个,30天完成任务,实际3天做了36个,照这样的速度加工,完成任务需要多少天?(用正、反比例解答)工作效率×工作时间=工作总量(一定)=解:设完成任务需要
=
=
=20
工作效率(一定)提升小结通过这节课的整理与复习,你有什么收获?
