2021-2022学年华东师大版八年级下册数学 第二十章数据的整理与初步处理 单元测试卷(word版 含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级下册数学 第二十章数据的整理与初步处理 单元测试卷(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 106.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 09:41:27 | ||
图片预览



文档简介
新华师大版八年级下册数学
第20章 数据的整理与初步处理单元测试题
时间:100分钟 总分:120分 姓名____________
一、选择题(每小题3分,共30分)
1. 如果一组数据的平均数为5,那么数据为 【 】
(A)8 (B)5 (C)4 (D)3
2. 如果的平均数为6,那么的平均数是 【 】
(A)4 (B)5 (C)6 (D)8
3. 已知数据的平均数为则的平均数为 【 】
(A) (B) (C) (D)
4. 一组数据10, 5, 15, 5,20,则这组数据的平均数和中位数分别是 【 】
(A)10, 10 (B)10, 12.5 (C)11, 12.5 (D)11, 10
5. 已知一组从小到大排列的数据的中位数是5,那么的值等于 【 】
(A)5 (B)6 (C)7 (D)8
6. 在一次体育测试中,小芳所在小组8个人的成绩(单位:分)分别是46 , 47 , 48 , 48 , 49 , 49 , 49 , 50,则这8个人成绩的中位数是 【 】
(A)47分 (B)48分 (C)48.5分 (D)49分
7. 已知一组数据的众数是则这组数据的中位数是 【 】
(A)9 (B)9.5 (C)3 (D)12
8. 在一次献爱心的捐赠活动中,某班45名同学捐款金额统计如下:
金额(元) 20 30 35 50 100
学生数(人) 5 10 5 15 10
在这次活动中,该班同学捐款金额的众数和中位数分别是 【 】
(A)30元, 35元 (B)50元, 35元
(C)50元, 50元 (D)15元, 50元
9. 若要对一射击运动员最近5次训练成绩进行统计分析,判断他的训练成绩是否稳定,则需要知道他5次训练成绩的 【 】
(A)中位数 (B)平均数 (C)众数 (D)方差
10. 某同学对甲、乙、丙、丁四个市场二月份每天的白菜价格进行调查,计算后发现这个月四个市场的价格平均值相同,方差分别为8.5, 2.5, 10.1 ,7.4 ,二月份白菜价格最稳定的市场是 【 】
(A)甲 (B)乙 (C)丙 (D)丁
二、填空题(每小题3分,共30分)
11. 在演唱比赛中,5名评委给一位歌手的打分如下:8.2分, 8.3分, 7.8分, 7.7分, 8.0分.则这位歌手的平均得分是________.
12. 某市号召市民节约用水,为了解居民用水情况,随机抽查了20户家庭某月的用水量,结果如下表,则这20户家庭这个月的平均用水量是________吨.
用水量(吨) 4 5 6 8
户数 3 8 4 5
13. 某校九年级(1)班40名同学中,14岁的有1人,15岁的有21人,16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是_______岁.
14. 若数据的平均数为,则
________.
15. 我市某一周的每一天的最高气温统计如下表:
最高气温(℃) 25 26 27 28
天数 1 1 2 3
则这组数据的中位数是________,众数是________.
16. 有5个从小到大排列的正整数,中位数是3,唯一的众数是8,则这5个数的和为________.
17. 某公司对应聘者进行面试,按专业知识、工作经验、仪表形象给应聘者打分,这三个方面的重要性之比为6 : 3 : 1 ,对应聘的王丽、张莹两人的打分如下表所示:
姓名 专业知识 工作经验 仪表形象
王丽 14 16 18
张莹 18 16 12
两人中只录取一个,若你是人事主管,你会录用____________.
18. 为筹备班级的毕业联欢会,班长对全班学生爱吃哪几种水果进行了民意调查,那么最终决定买什么水果,最值得关注的应该是统计调查数据的________(填中位数、众数或平均数).
19. 数据的方差是________.
20.随机从甲、乙两块试验田中各抽取100株麦苗测量高度,计算平均数和方差的结果为:,则小麦长势比较整齐的试验田是________.
三、解答题(每小题12分,共60分)
21. 为了解某小区居民的用水情况,随机抽取了该小区10户家庭的月用水量,结果如下表:
月用水量(吨) 10 13 14 17 18
户数 2 2 3 2 1
(1)计算这10户家庭的平均月用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用水多少吨.
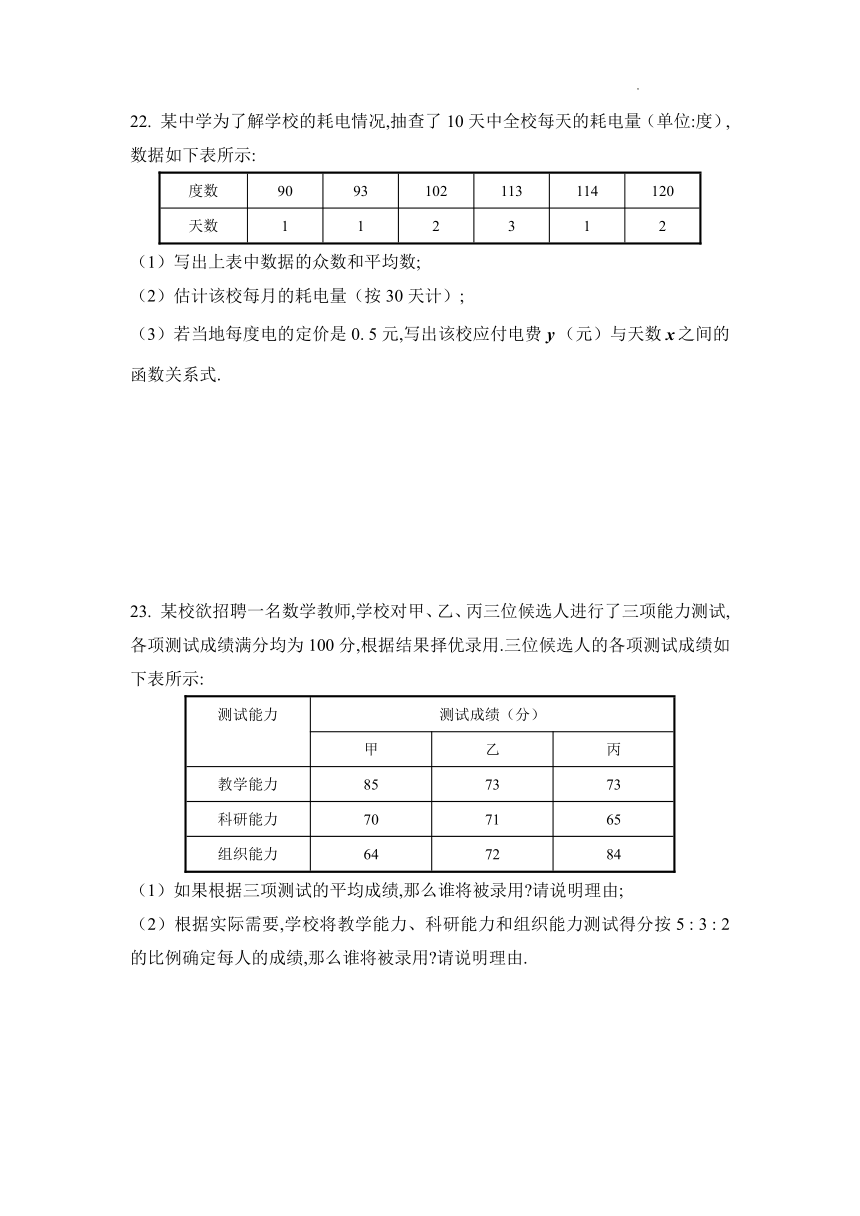
22. 某中学为了解学校的耗电情况,抽查了10天中全校每天的耗电量(单位:度),数据如下表所示:
度数 90 93 102 113 114 120
天数 1 1 2 3 1 2
(1)写出上表中数据的众数和平均数;
(2)估计该校每月的耗电量(按30天计);
(3)若当地每度电的定价是0. 5元,写出该校应付电费(元)与天数之间的函数关系式.
23. 某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
测试能力 测试成绩(分)
甲 乙 丙
教学能力 85 73 73
科研能力 70 71 65
组织能力 64 72 84
(1)如果根据三项测试的平均成绩,那么谁将被录用 请说明理由;
(2)根据实际需要,学校将教学能力、科研能力和组织能力测试得分按5 : 3 : 2的比例确定每人的成绩,那么谁将被录用 请说明理由.
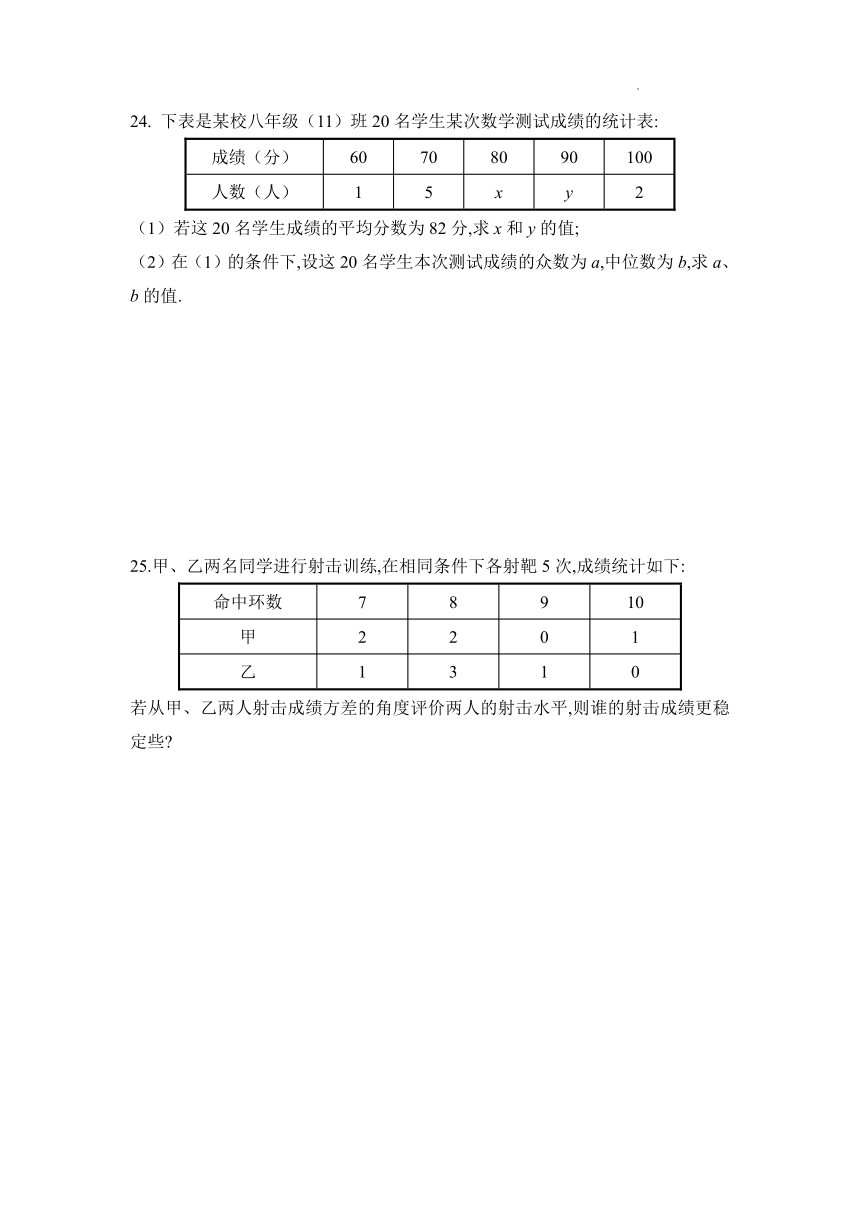
24. 下表是某校八年级(11)班20名学生某次数学测试成绩的统计表:
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
(1)若这20名学生成绩的平均分数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测试成绩的众数为a,中位数为b,求a、b的值.
25.甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下:
命中环数 7 8 9 10
甲 2 2 0 1
乙 1 3 1 0
若从甲、乙两人射击成绩方差的角度评价两人的射击水平,则谁的射击成绩更稳定些
新华师大版八年级下册数学
第20章 数据的整理与初步处理单元测试题参考答案
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5
答案 A D B D B
题号 6 7 8 9 10
答案 C A C D B
二、填空题(每小题3分,共30分)
11. 8分 12. 5. 8 13. 15 14. 0 15. 27℃ , 28℃
16. 22 17. 张莹 18. 众数 19. 6. 8 20. 甲
重要知识点总结:
本章介绍了几个非常重要的描述数据特性的概念,分别是:
(1)平均数(算术平均数) (2)加权平均数
(3)中位数 (4)众数 (5)方差
另外,我又给你们补充了一个概念:(6)极差.
平均数: 对于一组数据,其平均数用“”表示,计算公式为:
即一组数据的平均数等于数据的总和除以数据的个数.
平均数代表或表示了一组数据的平均水平.
关于平均数的结论: 介绍两个重要的结论:
(1)若一组数据中的每个数据都扩大相同的倍数,则该组数据的平均数也要扩大相同的倍数;
如:一组数据的平均数为,则数据的平均数便为.
(2)若两组数据:
的平均数分别为,则数据组:
的平均数为.
注意:要求两组数据含有相同的个数.
中位数: 一组数据,按从小到大的顺序排列之后,我们把处于最中间的那个数或最中间两个数的平均数叫做这组数据的中位数.
(1)若该组数据的个数为奇数,则最中间的数只有一个,作为这组的中位数;
(2)若该组数据的个数为偶数,则最中间的数有两个,把这两个数的平均数(即相加除以2)作为这组数据的作为中位数.
注意两点:(1)先排序,再确定中位数;
(2)一组数据的中位数必定存在,且只有一个.
众数: 把一组数据中出现次数最多的那个数据,叫做这组数据的众数.
注意:一组数据的众数可以没有(即不存在),也可以不止一个.
方差: 若一组数据的平均数为,则这组数据的方差计算公式为(方差用表示):
方差反映了一组数据的波动大小,方差越小,数据的波动也越小,数据反映的事实(如成绩、价格、物品质量等)越稳定.
最后注意 平均数、众数和中位数要带上和原数据一致的单位.
14.若数据的平均数为,则
________.
解析:∵数据的平均数为
∴
∴
21.解:(1)(吨)
即这10户家庭的平均月用水量为14吨;
(2)(吨)
即该小区居民每月共用水7000吨.
22.解:(1)众数为113度,
平均数为:(度);
(2)(度)
即该校每月的耗电量为3240度;
(3).
23.解:(1)(分)
(分)
(分)
∵74>73>72
∴丙将被录用;
(2)甲的得分:分
乙的得分:分
丙的得分:分
∵76.3 > 72.8 > 72.2
∴甲将被录用.
24.解:(1)由题意可得方程组:
整理得:
解之得:; (2)分,分.
25.解:分
分
∴
∵,∴乙的射击水平更稳定些.
第20章 数据的整理与初步处理单元测试题
时间:100分钟 总分:120分 姓名____________
一、选择题(每小题3分,共30分)
1. 如果一组数据的平均数为5,那么数据为 【 】
(A)8 (B)5 (C)4 (D)3
2. 如果的平均数为6,那么的平均数是 【 】
(A)4 (B)5 (C)6 (D)8
3. 已知数据的平均数为则的平均数为 【 】
(A) (B) (C) (D)
4. 一组数据10, 5, 15, 5,20,则这组数据的平均数和中位数分别是 【 】
(A)10, 10 (B)10, 12.5 (C)11, 12.5 (D)11, 10
5. 已知一组从小到大排列的数据的中位数是5,那么的值等于 【 】
(A)5 (B)6 (C)7 (D)8
6. 在一次体育测试中,小芳所在小组8个人的成绩(单位:分)分别是46 , 47 , 48 , 48 , 49 , 49 , 49 , 50,则这8个人成绩的中位数是 【 】
(A)47分 (B)48分 (C)48.5分 (D)49分
7. 已知一组数据的众数是则这组数据的中位数是 【 】
(A)9 (B)9.5 (C)3 (D)12
8. 在一次献爱心的捐赠活动中,某班45名同学捐款金额统计如下:
金额(元) 20 30 35 50 100
学生数(人) 5 10 5 15 10
在这次活动中,该班同学捐款金额的众数和中位数分别是 【 】
(A)30元, 35元 (B)50元, 35元
(C)50元, 50元 (D)15元, 50元
9. 若要对一射击运动员最近5次训练成绩进行统计分析,判断他的训练成绩是否稳定,则需要知道他5次训练成绩的 【 】
(A)中位数 (B)平均数 (C)众数 (D)方差
10. 某同学对甲、乙、丙、丁四个市场二月份每天的白菜价格进行调查,计算后发现这个月四个市场的价格平均值相同,方差分别为8.5, 2.5, 10.1 ,7.4 ,二月份白菜价格最稳定的市场是 【 】
(A)甲 (B)乙 (C)丙 (D)丁
二、填空题(每小题3分,共30分)
11. 在演唱比赛中,5名评委给一位歌手的打分如下:8.2分, 8.3分, 7.8分, 7.7分, 8.0分.则这位歌手的平均得分是________.
12. 某市号召市民节约用水,为了解居民用水情况,随机抽查了20户家庭某月的用水量,结果如下表,则这20户家庭这个月的平均用水量是________吨.
用水量(吨) 4 5 6 8
户数 3 8 4 5
13. 某校九年级(1)班40名同学中,14岁的有1人,15岁的有21人,16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是_______岁.
14. 若数据的平均数为,则
________.
15. 我市某一周的每一天的最高气温统计如下表:
最高气温(℃) 25 26 27 28
天数 1 1 2 3
则这组数据的中位数是________,众数是________.
16. 有5个从小到大排列的正整数,中位数是3,唯一的众数是8,则这5个数的和为________.
17. 某公司对应聘者进行面试,按专业知识、工作经验、仪表形象给应聘者打分,这三个方面的重要性之比为6 : 3 : 1 ,对应聘的王丽、张莹两人的打分如下表所示:
姓名 专业知识 工作经验 仪表形象
王丽 14 16 18
张莹 18 16 12
两人中只录取一个,若你是人事主管,你会录用____________.
18. 为筹备班级的毕业联欢会,班长对全班学生爱吃哪几种水果进行了民意调查,那么最终决定买什么水果,最值得关注的应该是统计调查数据的________(填中位数、众数或平均数).
19. 数据的方差是________.
20.随机从甲、乙两块试验田中各抽取100株麦苗测量高度,计算平均数和方差的结果为:,则小麦长势比较整齐的试验田是________.
三、解答题(每小题12分,共60分)
21. 为了解某小区居民的用水情况,随机抽取了该小区10户家庭的月用水量,结果如下表:
月用水量(吨) 10 13 14 17 18
户数 2 2 3 2 1
(1)计算这10户家庭的平均月用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用水多少吨.
22. 某中学为了解学校的耗电情况,抽查了10天中全校每天的耗电量(单位:度),数据如下表所示:
度数 90 93 102 113 114 120
天数 1 1 2 3 1 2
(1)写出上表中数据的众数和平均数;
(2)估计该校每月的耗电量(按30天计);
(3)若当地每度电的定价是0. 5元,写出该校应付电费(元)与天数之间的函数关系式.
23. 某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
测试能力 测试成绩(分)
甲 乙 丙
教学能力 85 73 73
科研能力 70 71 65
组织能力 64 72 84
(1)如果根据三项测试的平均成绩,那么谁将被录用 请说明理由;
(2)根据实际需要,学校将教学能力、科研能力和组织能力测试得分按5 : 3 : 2的比例确定每人的成绩,那么谁将被录用 请说明理由.
24. 下表是某校八年级(11)班20名学生某次数学测试成绩的统计表:
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
(1)若这20名学生成绩的平均分数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测试成绩的众数为a,中位数为b,求a、b的值.
25.甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下:
命中环数 7 8 9 10
甲 2 2 0 1
乙 1 3 1 0
若从甲、乙两人射击成绩方差的角度评价两人的射击水平,则谁的射击成绩更稳定些
新华师大版八年级下册数学
第20章 数据的整理与初步处理单元测试题参考答案
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5
答案 A D B D B
题号 6 7 8 9 10
答案 C A C D B
二、填空题(每小题3分,共30分)
11. 8分 12. 5. 8 13. 15 14. 0 15. 27℃ , 28℃
16. 22 17. 张莹 18. 众数 19. 6. 8 20. 甲
重要知识点总结:
本章介绍了几个非常重要的描述数据特性的概念,分别是:
(1)平均数(算术平均数) (2)加权平均数
(3)中位数 (4)众数 (5)方差
另外,我又给你们补充了一个概念:(6)极差.
平均数: 对于一组数据,其平均数用“”表示,计算公式为:
即一组数据的平均数等于数据的总和除以数据的个数.
平均数代表或表示了一组数据的平均水平.
关于平均数的结论: 介绍两个重要的结论:
(1)若一组数据中的每个数据都扩大相同的倍数,则该组数据的平均数也要扩大相同的倍数;
如:一组数据的平均数为,则数据的平均数便为.
(2)若两组数据:
的平均数分别为,则数据组:
的平均数为.
注意:要求两组数据含有相同的个数.
中位数: 一组数据,按从小到大的顺序排列之后,我们把处于最中间的那个数或最中间两个数的平均数叫做这组数据的中位数.
(1)若该组数据的个数为奇数,则最中间的数只有一个,作为这组的中位数;
(2)若该组数据的个数为偶数,则最中间的数有两个,把这两个数的平均数(即相加除以2)作为这组数据的作为中位数.
注意两点:(1)先排序,再确定中位数;
(2)一组数据的中位数必定存在,且只有一个.
众数: 把一组数据中出现次数最多的那个数据,叫做这组数据的众数.
注意:一组数据的众数可以没有(即不存在),也可以不止一个.
方差: 若一组数据的平均数为,则这组数据的方差计算公式为(方差用表示):
方差反映了一组数据的波动大小,方差越小,数据的波动也越小,数据反映的事实(如成绩、价格、物品质量等)越稳定.
最后注意 平均数、众数和中位数要带上和原数据一致的单位.
14.若数据的平均数为,则
________.
解析:∵数据的平均数为
∴
∴
21.解:(1)(吨)
即这10户家庭的平均月用水量为14吨;
(2)(吨)
即该小区居民每月共用水7000吨.
22.解:(1)众数为113度,
平均数为:(度);
(2)(度)
即该校每月的耗电量为3240度;
(3).
23.解:(1)(分)
(分)
(分)
∵74>73>72
∴丙将被录用;
(2)甲的得分:分
乙的得分:分
丙的得分:分
∵76.3 > 72.8 > 72.2
∴甲将被录用.
24.解:(1)由题意可得方程组:
整理得:
解之得:; (2)分,分.
25.解:分
分
∴
∵,∴乙的射击水平更稳定些.
