2021-2022学年沪科版数学九年级下册24.6正多边形与圆 课后提升(word版 含解析)
文档属性
| 名称 | 2021-2022学年沪科版数学九年级下册24.6正多边形与圆 课后提升(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 00:00:00 | ||
图片预览


文档简介
正多边形与圆
一、单选题
1.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则( )
A.不能构成三角形 B.这个三角形是等边三角形
C.这个三角形是直角三角形 D.这个三角形是等腰三角形
2.正多边形的内切圆与外接圆的半径之比为,则这个正多边形为( )
A.正十二边形 B.正六边形 C.正四边形 D.正三角形
3.如图,△ABC是圆O的内接正三角形,弦EF过BC的中点D,且EF∥AB,若AB=4,则DE的长为( )
A.1 B.﹣1 C. D.2
4.如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,若DF恰好是同圆的一个内接正n边形的一边,则n的值为( )
A.6 B.8 C.10 D.12
5.如图,正六边形ABCDEF内接于,已知的 半径为2,则圆心O到边AB的距离是( )
A.2 B.1 C. D.
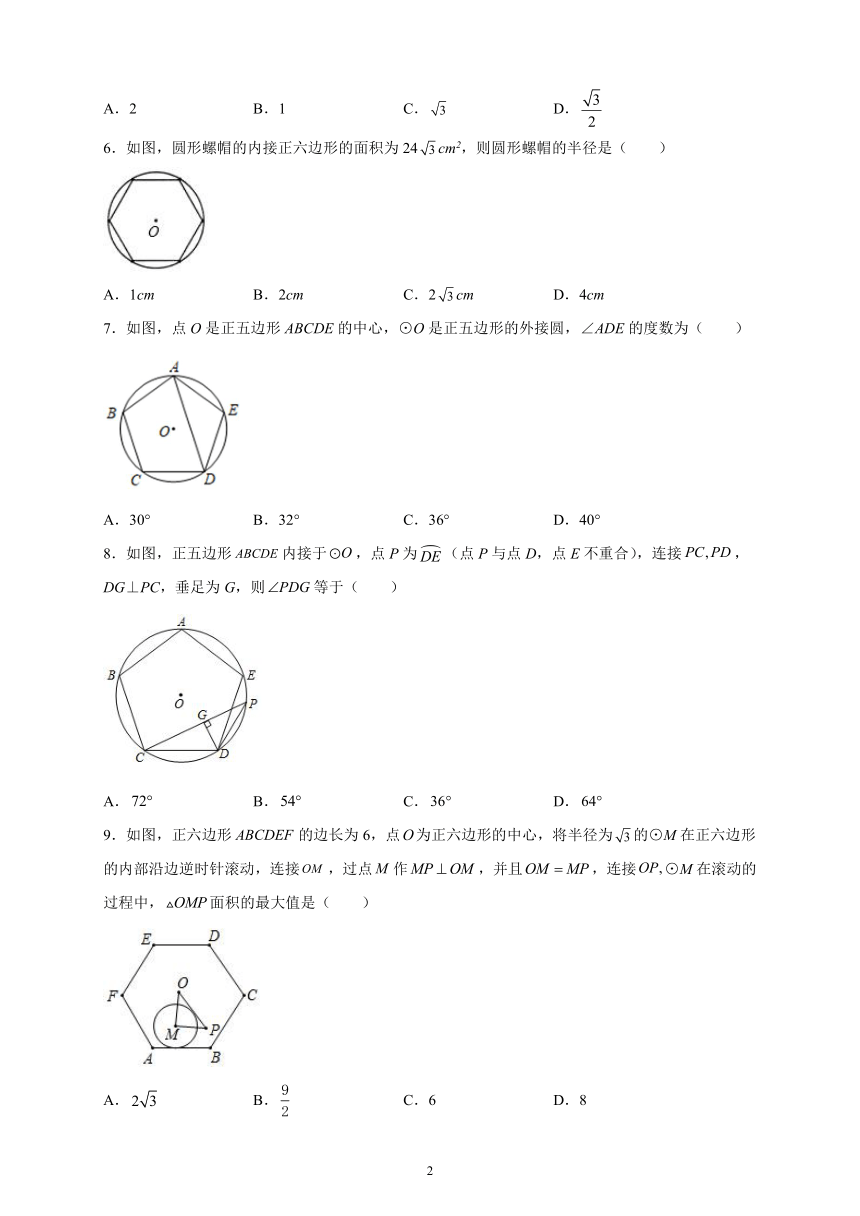
6.如图,圆形螺帽的内接正六边形的面积为24cm2,则圆形螺帽的半径是( )
A.1cm B.2cm C.2cm D.4cm
7.如图,点O是正五边形ABCDE的中心,⊙O是正五边形的外接圆,∠ADE的度数为( )
A.30° B.32° C.36° D.40°
8.如图,正五边形内接于,点P为(点P与点D,点E不重合),连接,DG⊥PC,垂足为G,则等于( )
A. B. C. D.
9.如图,正六边形的边长为6,点为正六边形的中心,将半径为的⊙M在正六边形的内部沿边逆时针滚动,连接,过点作,并且,连接⊙M在滚动的过程中,面积的最大值是( )
A. B. C.6 D.8
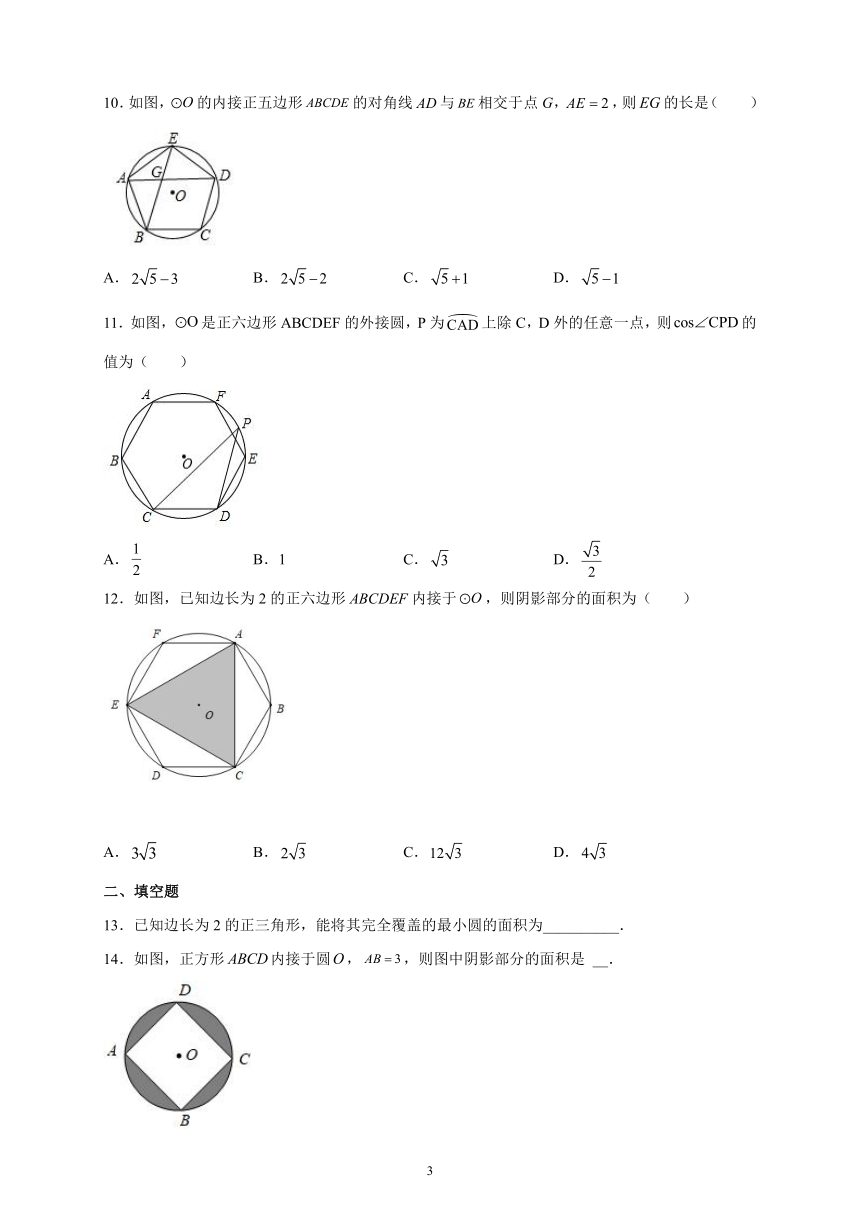
10.如图,的内接正五边形的对角线与相交于点G,,则的长是( )
A. B. C. D.
11.如图,是正六边形ABCDEF的外接圆,P为上除C,D外的任意一点,则的值为( )
A. B.1 C. D.
12.如图,已知边长为2的正六边形ABCDEF内接于,则阴影部分的面积为( )
A. B. C. D.
二、填空题
13.已知边长为2的正三角形,能将其完全覆盖的最小圆的面积为__________.
14.如图,正方形内接于圆,,则图中阴影部分的面积是 __.
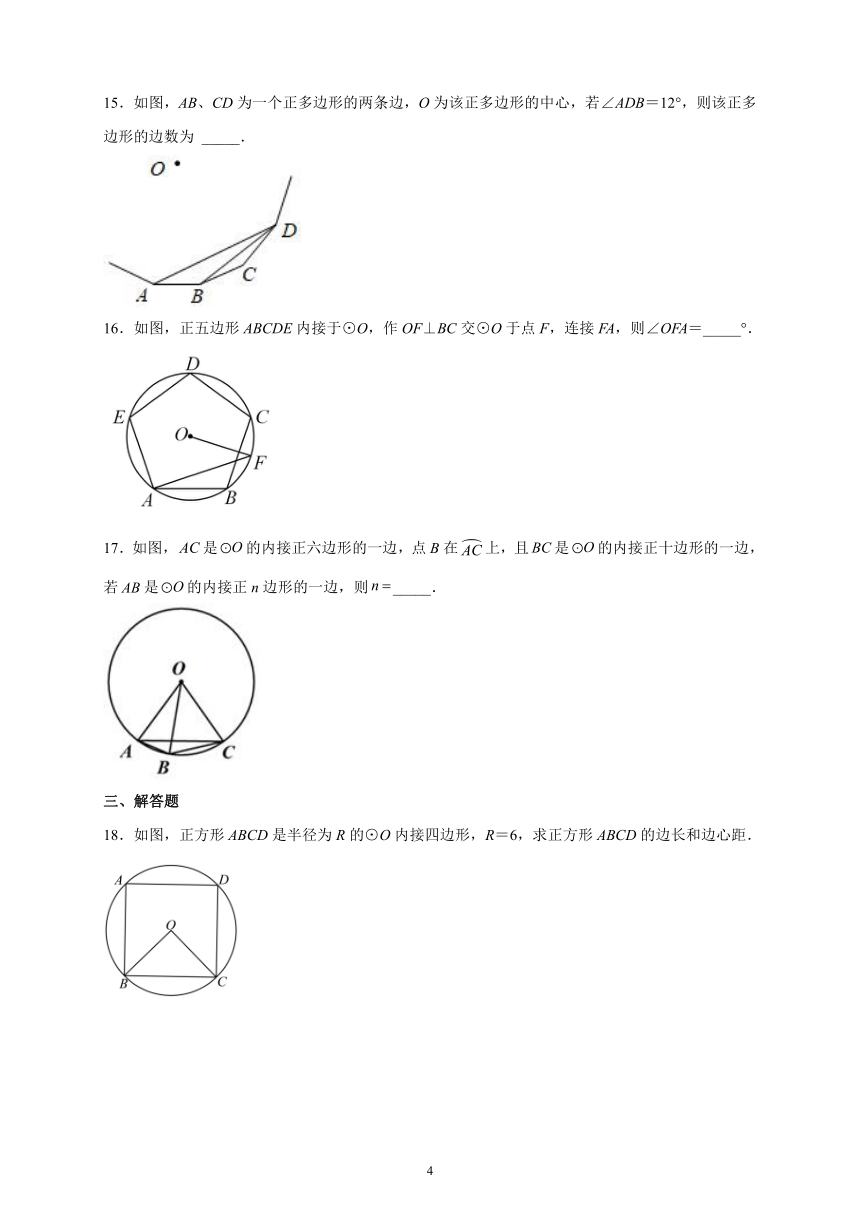
15.如图,AB、CD为一个正多边形的两条边,O为该正多边形的中心,若∠ADB=12°,则该正多边形的边数为 _____.
16.如图,正五边形ABCDE内接于⊙O,作OF⊥BC交⊙O于点F,连接FA,则∠OFA=_____°.
17.如图,是的内接正六边形的一边,点B在上,且是的内接正十边形的一边,若是的内接正n边形的一边,则_____.
三、解答题
18.如图,正方形ABCD是半径为R的⊙O内接四边形,R=6,求正方形ABCD的边长和边心距.
19.如图,在圆内接正三角形中,若∠DOE保持120°角度不变,求证:当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形,图中阴影部分的面积始终是△ABC的面积的.
20.如图,的半径为R,正方形,正方形分别是的内接正方形和外切正方形.求二者的边长比和面积比.
21.如图所示,正三角形ABC、正方形ABCD、正五边形ABCDE分别是的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度在上逆时针运动.
(1)求图①中的度数
(2)图②中的度数是______,图③中的度数是______;
(3)若推广到一般的正n边形情况,请写出的度数是______.
22.德国著名的天文学家开普勒说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿”.
如图①,点C把线段分成两部分,如果,那么称点C为线段的黄金分割点.
(1)特例感知:在图①中,若,求的长;
(2)知识探究:如图②,作⊙O的内接正五边形:
①作两条相互垂直的直径、;
②作的中点P,以P为圆心,为半径画弧交于点Q;
③以点A为圆心,为半径,在⊙O上连续截取等弧,使弦,连接;
则五边形为正五边形.
在该正五边形作法中,点Q是否为线段的黄金分割点?请说明理由.
(3)拓展应用:国旗和国徽上的五角星是革命和光明的象征,是一个非常优美的几何图形,与黄金分割有着密切的联系.
延长题(2)中的正五边形的每条边,相交可得到五角星,摆正后如图③,点E是线段的黄金分割点,请利用题中的条件,求的值.
试卷第1页,共3页
参考答案:
1.C
解:如图,∵正三角形、正方形、正六边形都内接于半径为1的圆,边心距分别为OC,OE,OG,OA=1,∠AOC=60°,∠AOE=45°,∠AOG=30°,
∴OC=OAcos60°=,OE= OAcos45°=,OG= OAcos30°=,
∵,
∴这个三角形是直角三角形,
故选C.
2.C
解:正多边形的内切圆与外接圆的半径之比为,
设AB是正多边形的一边,OC⊥AB,
则OC=,OA=OB=2,
在Rt△AOC中,cos∠AOC==,
∴∠AOC=45°,
∴∠AOB=90°,
则正多边形边数是:=4.
故选:C.
3.B
解:如图,连接交于点,连接,,,
△ABC是圆O的内接正三角形,
,,
,
,
是BC的中点,
,
,
,
是BC的中点,AB=4,
,
设,则(),
,
即,
解得,
,
,
,
在中
,
.
故选B.
4.D
解:如图,连接,
四边形为的内接正四边形,为的内接正三角形,
点在上,且是和的角平分线,,
,
,
,
恰好是圆O的一个内接正边形的一边,
,
故选:D.
5.C
解:过O作OH⊥AB于H,
在正六边形ABCDEF中,∠AOB= =60°,
∵OA=OB,
∴∠AOH=30°,AH=AB=1,
∴OH=AH=,
故选C.
6.D
解:如图,由圆内接正六边形的性质可得△AOB是正三角形,过作于
设半径为r,即OA=OB=AB=r,
OM=OA sin∠OAB=,
∵圆O的内接正六边形的面积为(cm2),
∴△AOB的面积为(cm2),
即,
,
解得r=4,
故选:D.
7.C
解:
如上图所示,连接OA,OE
∵五边形ABCDE是正五边形
∴
∵⊙O是正五边形ABCDE的外接圆
∴
故选:C.
8.B
解:连接OC,OD.
在正五边形ABCDE中,∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°-36°=54°,
故选:B.
9.D
解:当与正六边形的两边AB、BC相切时,OM值最大,
设与AB相切于点N,连接MN,OA,如图所示:
∵是等边三角形,
∴,,
在中,∵,,
∴,,
∴,
∴面积的最大值,
故选:D.
10.D
解:在⊙O的内接正五边形ABCDE中,设EG=x,
易知:∠AEB=∠ABE=∠EAG=36°,∠BAG=∠AGB=72°,
∴AB=BG=AE=2,
∵∠AEG=∠AEB,∠EAG=∠EBA,
∴△AEG∽△BEA,
∴,
∴AE2=EG EB,
∴,
解得x= 1+或x= 1 (舍去).
∴EG=-1.
故选:D.
11.D
解:连接OC、OD,如图所示:
∵是正六边形ABCDEF的外接圆,
∴,
P为上除C,D外的任意一点,
∴,
∴,
故选:D.
12.A
解:连接OE、OC,过点O作OH CE于H
在六边形ABCDEF中
AF=FE=DE=DC=CB=AB
同理,
是等边三角形
阴影部分的面积=3
故选:A.
13.##
解:如图,为等边三角形,为的外心,
过点,
故答案为:
14.
解:连接、,
四边形是正方形,
,,
.
所以阴影部分的面积.
故选:.
15.15##十五
解:如图,设正多边形的外接圆为⊙O,连接OA,OB,
∵∠ADB=12°,
∴∠AOB=2∠ADB=24°,
而360°÷24°=15,
∴这个正多边形为正十五边形,
故答案为:15.
16.36
解:连接OA,OB,OB交AF于J.
∵五边形ABCDE是正五边形,OF⊥BC,
∴,
∴∠AOB=72°,∠BOF=∠AOB=36°,
∴∠AOF=∠AOB +∠BOF=108°,
∵OA=OF,
∴∠OAF=∠OFA==36°
故答案为:36.
17.15
解:∵是的内接正六边形的一边,是的内接正十边形的一边,
∴,
∴,
∵是的内接正n边形的一边,
∴
故答案为:15.
18.边长为,边心距为
解:过点O作OE⊥BC,垂足为E,
∵正方形ABCD是半径为R的⊙O内接四边形,R=6,
∴∠BOC==90°,∠OBC=45°,OB=OC=6,
∴BE=OE.
在Rt△OBE中,∠BEO=90°,由勾股定理可得
∵OE2+BE2=OB2,
∴OE2+BE2=36,
∴OE= BE=,
∴BC=2BE=,
即半径为6的圆内接正方形ABCD的边长为,边心距为.
19.见解析
解:如图:连接OA、OB、OC,
由正多边形和圆的性质可得△OAB≌△OBC≌△OCA.
∴ ∠1=∠2.
设OD交BC于F,OE交AC于G,则∠AOC=∠3+∠4=120°,
∠DOE=∠5+∠4=120°,
∴ ∠3=∠5.
在△OAG和△OCF中,
∴ △OAG≌△OCF.
∴ .
20.,
解:连接OA,过点O作OM⊥AD于D,
∵的半径为R,
∴OA=R,
∵正方形是的内接正方形,
∴,
∴△OAM是等腰直角三角形,,
∴,,
∴ =,
∴=.
.
21.(1)120°;(2)90°,72°;(3)
解:(1)∵是正三角形,
∴,
∵点M、N分别从点B、C开始以相同的速度在上逆时针运动,
∴,
∴,
∴;
(2)由图②,四边形ABCD是正方形,则与(1)同理,
,
∴;
由图③,正五边形ABCDE中,与(1)同理,
∴,
∴;
故答案为:90°;72°;
(3)由(1)可知,∠APB为所在正多边形的外角度数,故在图n中,有∠APB=;
故答案为:;
22.(1)61.8;(2)是,理由见解析;(3)
解:(1)∵,
∴,
即,
解得:AC≈61.8;
(2)Q是线段OM的黄金分割点,理由如下:
设⊙O的半径为a,则OA=ON=OM=a,
∴OP=,
∴,
∴OQ=PQ-OP=,
∴MQ=OM-OQ=,
,
∴Q是线段OM的黄金分割点;
(3)正五边形的每个内角为:,
∴∠PEA=∠PAE=,
∴cos72°=,
∵点E是线段PD的黄金分割点,
∴,
又∵AE=ED,
∴,
∴cos72°=.
答案第1页,共2页
一、单选题
1.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则( )
A.不能构成三角形 B.这个三角形是等边三角形
C.这个三角形是直角三角形 D.这个三角形是等腰三角形
2.正多边形的内切圆与外接圆的半径之比为,则这个正多边形为( )
A.正十二边形 B.正六边形 C.正四边形 D.正三角形
3.如图,△ABC是圆O的内接正三角形,弦EF过BC的中点D,且EF∥AB,若AB=4,则DE的长为( )
A.1 B.﹣1 C. D.2
4.如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,若DF恰好是同圆的一个内接正n边形的一边,则n的值为( )
A.6 B.8 C.10 D.12
5.如图,正六边形ABCDEF内接于,已知的 半径为2,则圆心O到边AB的距离是( )
A.2 B.1 C. D.
6.如图,圆形螺帽的内接正六边形的面积为24cm2,则圆形螺帽的半径是( )
A.1cm B.2cm C.2cm D.4cm
7.如图,点O是正五边形ABCDE的中心,⊙O是正五边形的外接圆,∠ADE的度数为( )
A.30° B.32° C.36° D.40°
8.如图,正五边形内接于,点P为(点P与点D,点E不重合),连接,DG⊥PC,垂足为G,则等于( )
A. B. C. D.
9.如图,正六边形的边长为6,点为正六边形的中心,将半径为的⊙M在正六边形的内部沿边逆时针滚动,连接,过点作,并且,连接⊙M在滚动的过程中,面积的最大值是( )
A. B. C.6 D.8
10.如图,的内接正五边形的对角线与相交于点G,,则的长是( )
A. B. C. D.
11.如图,是正六边形ABCDEF的外接圆,P为上除C,D外的任意一点,则的值为( )
A. B.1 C. D.
12.如图,已知边长为2的正六边形ABCDEF内接于,则阴影部分的面积为( )
A. B. C. D.
二、填空题
13.已知边长为2的正三角形,能将其完全覆盖的最小圆的面积为__________.
14.如图,正方形内接于圆,,则图中阴影部分的面积是 __.
15.如图,AB、CD为一个正多边形的两条边,O为该正多边形的中心,若∠ADB=12°,则该正多边形的边数为 _____.
16.如图,正五边形ABCDE内接于⊙O,作OF⊥BC交⊙O于点F,连接FA,则∠OFA=_____°.
17.如图,是的内接正六边形的一边,点B在上,且是的内接正十边形的一边,若是的内接正n边形的一边,则_____.
三、解答题
18.如图,正方形ABCD是半径为R的⊙O内接四边形,R=6,求正方形ABCD的边长和边心距.
19.如图,在圆内接正三角形中,若∠DOE保持120°角度不变,求证:当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形,图中阴影部分的面积始终是△ABC的面积的.
20.如图,的半径为R,正方形,正方形分别是的内接正方形和外切正方形.求二者的边长比和面积比.
21.如图所示,正三角形ABC、正方形ABCD、正五边形ABCDE分别是的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度在上逆时针运动.
(1)求图①中的度数
(2)图②中的度数是______,图③中的度数是______;
(3)若推广到一般的正n边形情况,请写出的度数是______.
22.德国著名的天文学家开普勒说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿”.
如图①,点C把线段分成两部分,如果,那么称点C为线段的黄金分割点.
(1)特例感知:在图①中,若,求的长;
(2)知识探究:如图②,作⊙O的内接正五边形:
①作两条相互垂直的直径、;
②作的中点P,以P为圆心,为半径画弧交于点Q;
③以点A为圆心,为半径,在⊙O上连续截取等弧,使弦,连接;
则五边形为正五边形.
在该正五边形作法中,点Q是否为线段的黄金分割点?请说明理由.
(3)拓展应用:国旗和国徽上的五角星是革命和光明的象征,是一个非常优美的几何图形,与黄金分割有着密切的联系.
延长题(2)中的正五边形的每条边,相交可得到五角星,摆正后如图③,点E是线段的黄金分割点,请利用题中的条件,求的值.
试卷第1页,共3页
参考答案:
1.C
解:如图,∵正三角形、正方形、正六边形都内接于半径为1的圆,边心距分别为OC,OE,OG,OA=1,∠AOC=60°,∠AOE=45°,∠AOG=30°,
∴OC=OAcos60°=,OE= OAcos45°=,OG= OAcos30°=,
∵,
∴这个三角形是直角三角形,
故选C.
2.C
解:正多边形的内切圆与外接圆的半径之比为,
设AB是正多边形的一边,OC⊥AB,
则OC=,OA=OB=2,
在Rt△AOC中,cos∠AOC==,
∴∠AOC=45°,
∴∠AOB=90°,
则正多边形边数是:=4.
故选:C.
3.B
解:如图,连接交于点,连接,,,
△ABC是圆O的内接正三角形,
,,
,
,
是BC的中点,
,
,
,
是BC的中点,AB=4,
,
设,则(),
,
即,
解得,
,
,
,
在中
,
.
故选B.
4.D
解:如图,连接,
四边形为的内接正四边形,为的内接正三角形,
点在上,且是和的角平分线,,
,
,
,
恰好是圆O的一个内接正边形的一边,
,
故选:D.
5.C
解:过O作OH⊥AB于H,
在正六边形ABCDEF中,∠AOB= =60°,
∵OA=OB,
∴∠AOH=30°,AH=AB=1,
∴OH=AH=,
故选C.
6.D
解:如图,由圆内接正六边形的性质可得△AOB是正三角形,过作于
设半径为r,即OA=OB=AB=r,
OM=OA sin∠OAB=,
∵圆O的内接正六边形的面积为(cm2),
∴△AOB的面积为(cm2),
即,
,
解得r=4,
故选:D.
7.C
解:
如上图所示,连接OA,OE
∵五边形ABCDE是正五边形
∴
∵⊙O是正五边形ABCDE的外接圆
∴
故选:C.
8.B
解:连接OC,OD.
在正五边形ABCDE中,∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°-36°=54°,
故选:B.
9.D
解:当与正六边形的两边AB、BC相切时,OM值最大,
设与AB相切于点N,连接MN,OA,如图所示:
∵是等边三角形,
∴,,
在中,∵,,
∴,,
∴,
∴面积的最大值,
故选:D.
10.D
解:在⊙O的内接正五边形ABCDE中,设EG=x,
易知:∠AEB=∠ABE=∠EAG=36°,∠BAG=∠AGB=72°,
∴AB=BG=AE=2,
∵∠AEG=∠AEB,∠EAG=∠EBA,
∴△AEG∽△BEA,
∴,
∴AE2=EG EB,
∴,
解得x= 1+或x= 1 (舍去).
∴EG=-1.
故选:D.
11.D
解:连接OC、OD,如图所示:
∵是正六边形ABCDEF的外接圆,
∴,
P为上除C,D外的任意一点,
∴,
∴,
故选:D.
12.A
解:连接OE、OC,过点O作OH CE于H
在六边形ABCDEF中
AF=FE=DE=DC=CB=AB
同理,
是等边三角形
阴影部分的面积=3
故选:A.
13.##
解:如图,为等边三角形,为的外心,
过点,
故答案为:
14.
解:连接、,
四边形是正方形,
,,
.
所以阴影部分的面积.
故选:.
15.15##十五
解:如图,设正多边形的外接圆为⊙O,连接OA,OB,
∵∠ADB=12°,
∴∠AOB=2∠ADB=24°,
而360°÷24°=15,
∴这个正多边形为正十五边形,
故答案为:15.
16.36
解:连接OA,OB,OB交AF于J.
∵五边形ABCDE是正五边形,OF⊥BC,
∴,
∴∠AOB=72°,∠BOF=∠AOB=36°,
∴∠AOF=∠AOB +∠BOF=108°,
∵OA=OF,
∴∠OAF=∠OFA==36°
故答案为:36.
17.15
解:∵是的内接正六边形的一边,是的内接正十边形的一边,
∴,
∴,
∵是的内接正n边形的一边,
∴
故答案为:15.
18.边长为,边心距为
解:过点O作OE⊥BC,垂足为E,
∵正方形ABCD是半径为R的⊙O内接四边形,R=6,
∴∠BOC==90°,∠OBC=45°,OB=OC=6,
∴BE=OE.
在Rt△OBE中,∠BEO=90°,由勾股定理可得
∵OE2+BE2=OB2,
∴OE2+BE2=36,
∴OE= BE=,
∴BC=2BE=,
即半径为6的圆内接正方形ABCD的边长为,边心距为.
19.见解析
解:如图:连接OA、OB、OC,
由正多边形和圆的性质可得△OAB≌△OBC≌△OCA.
∴ ∠1=∠2.
设OD交BC于F,OE交AC于G,则∠AOC=∠3+∠4=120°,
∠DOE=∠5+∠4=120°,
∴ ∠3=∠5.
在△OAG和△OCF中,
∴ △OAG≌△OCF.
∴ .
20.,
解:连接OA,过点O作OM⊥AD于D,
∵的半径为R,
∴OA=R,
∵正方形是的内接正方形,
∴,
∴△OAM是等腰直角三角形,,
∴,,
∴ =,
∴=.
.
21.(1)120°;(2)90°,72°;(3)
解:(1)∵是正三角形,
∴,
∵点M、N分别从点B、C开始以相同的速度在上逆时针运动,
∴,
∴,
∴;
(2)由图②,四边形ABCD是正方形,则与(1)同理,
,
∴;
由图③,正五边形ABCDE中,与(1)同理,
∴,
∴;
故答案为:90°;72°;
(3)由(1)可知,∠APB为所在正多边形的外角度数,故在图n中,有∠APB=;
故答案为:;
22.(1)61.8;(2)是,理由见解析;(3)
解:(1)∵,
∴,
即,
解得:AC≈61.8;
(2)Q是线段OM的黄金分割点,理由如下:
设⊙O的半径为a,则OA=ON=OM=a,
∴OP=,
∴,
∴OQ=PQ-OP=,
∴MQ=OM-OQ=,
,
∴Q是线段OM的黄金分割点;
(3)正五边形的每个内角为:,
∴∠PEA=∠PAE=,
∴cos72°=,
∵点E是线段PD的黄金分割点,
∴,
又∵AE=ED,
∴,
∴cos72°=.
答案第1页,共2页
