2021-2022学年沪科版数学九年级下册24.7弧长与扇形面积 课后提升(word版 含解析)
文档属性
| 名称 | 2021-2022学年沪科版数学九年级下册24.7弧长与扇形面积 课后提升(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 599.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 09:44:18 | ||
图片预览



文档简介
弧长与扇形面积
一、单选题
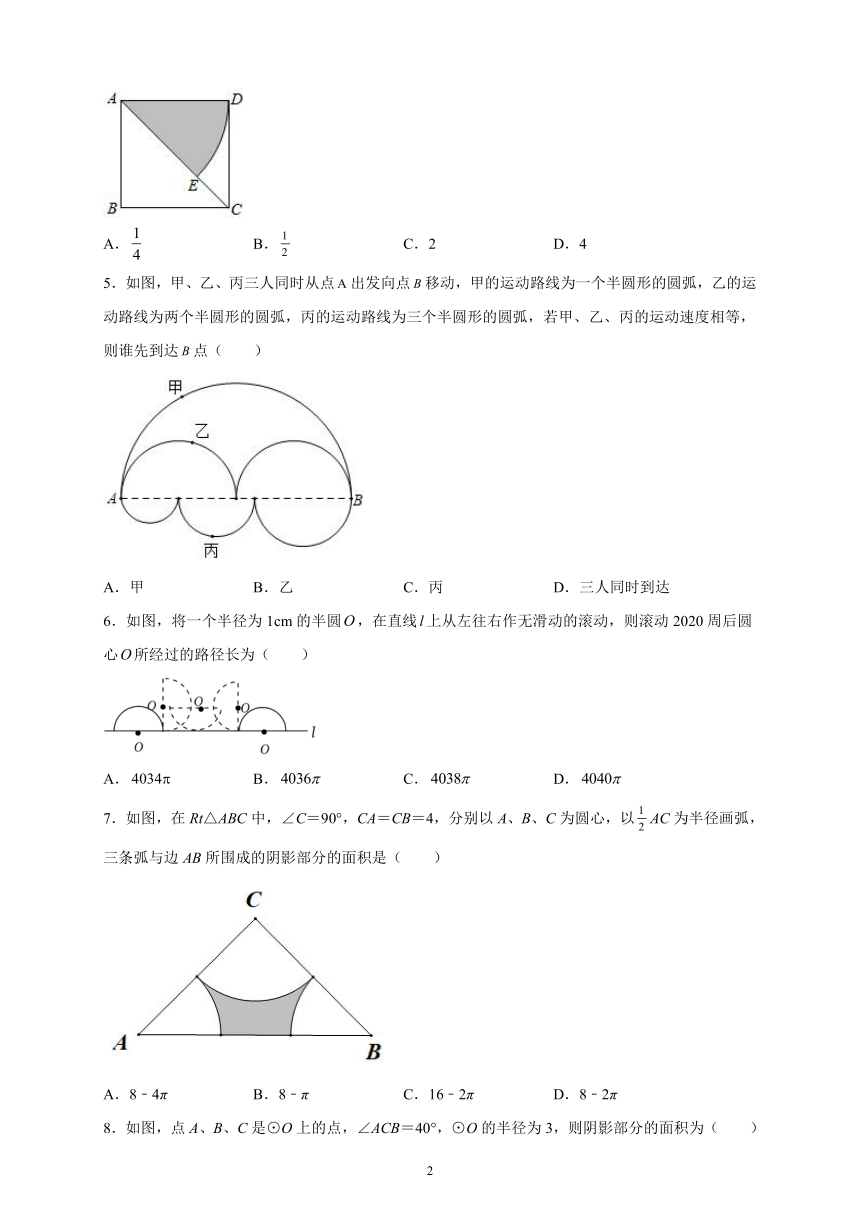
1.如图,在扇形纸片中,,,在桌面内的直线上,现将此扇形沿按顺时针方向旋转(旋转过程中无滑动),当落在上时,停止旋转.则点所经过的路线长为( )
A. B. C. D.
2.如图,在中,,,.将绕直角顶点逆时针旋转得△;则点转过的路径长为( )
A. B. C. D.
3.已知水平放置半径为6cm的球形容器中装有溶液,容器内液面的面积为cm2,如图,是该球体的一个最大纵截面,则该截面中阴影部分的弧长为( )
A.cm B.cm C.cm D.cm
4.如图,正方形ABCD的边长为4,以点A为圆心,AD为半径,画圆弧DE得到扇形DAE(阴影部分,点E在对角线AC上),若扇形DAE正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A. B. C.2 D.4
5.如图,甲、乙、丙三人同时从点出发向点移动,甲的运动路线为一个半圆形的圆弧,乙的运动路线为两个半圆形的圆弧,丙的运动路线为三个半圆形的圆弧,若甲、乙、丙的运动速度相等,则谁先到达点( )
A.甲 B.乙 C.丙 D.三人同时到达
6.如图,将一个半径为1cm的半圆,在直线上从左往右作无滑动的滚动,则滚动2020周后圆心所经过的路径长为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A、B、C为圆心,以AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是( )
A.8﹣4π B.8﹣π C.16﹣2π D.8﹣2π
8.如图,点A、B、C是⊙O上的点,∠ACB=40°,⊙O的半径为3,则阴影部分的面积为( )
A.π B.2π C.3π D.4π
9.如图,在矩形ABCD中,AD=2,AB=1,以A为圆心,AD的长为半径画弧交BC于点E,则图中空白部分的面积是( )
A.1﹣ B.2﹣ C. D.2+
10.如图,在⊙O的内接正六边形ABCDEF中,AB=,则图中阴影部分的面积为( )
A. B. C. D.
11.如图,AB和CD是⊙O的两条互相垂直的弦,若AD=4,BC=2,则阴影部分的面积是( )
A.2π﹣1 B.π﹣4 C.5π﹣4 D.5π﹣8
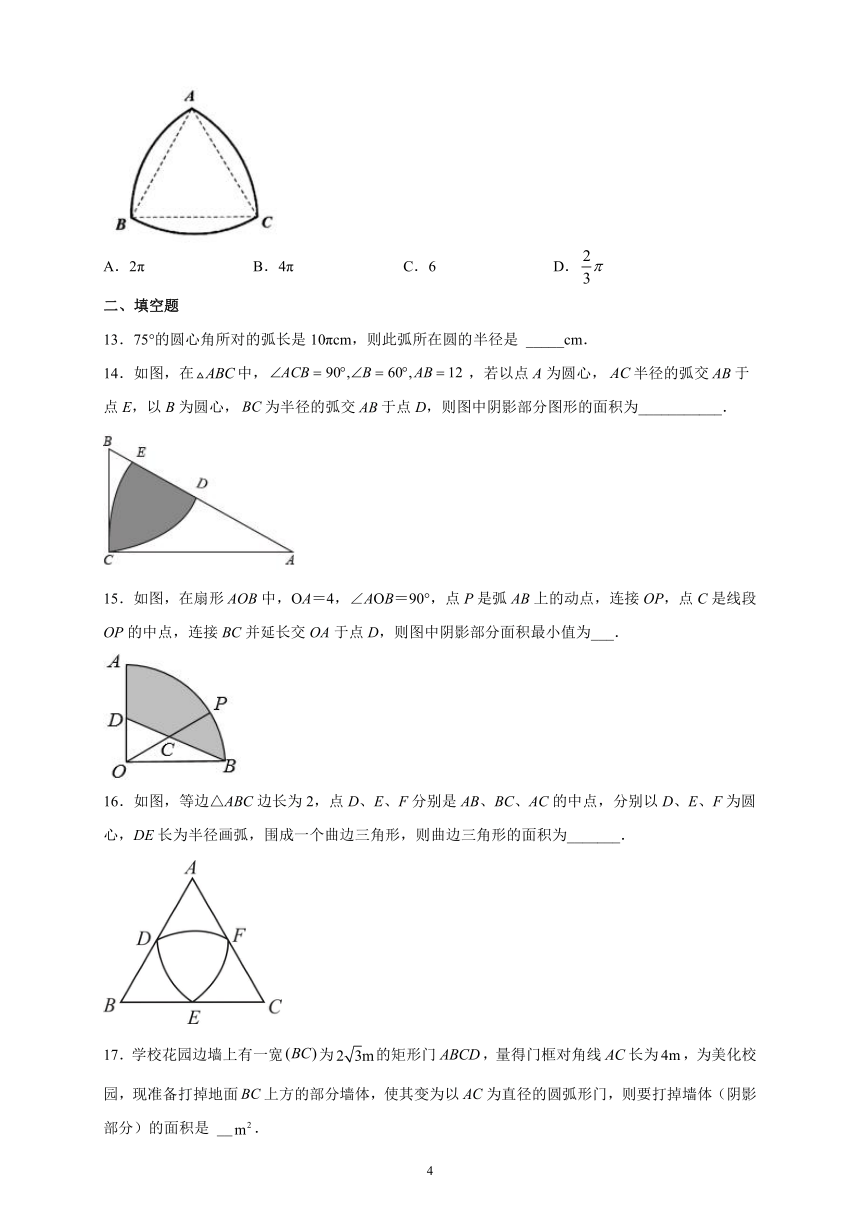
12.如图,分别以等边△ABC的三个顶点为圆心,边长为半径画弧,得到的封闭图形是莱洛三角形.若AB=2,则此莱洛三角形的周长为( )
A.2π B.4π C.6 D.
二、填空题
13.75°的圆心角所对的弧长是10πcm,则此弧所在圆的半径是 _____cm.
14.如图,在中,,若以点A为圆心,半径的弧交于点E,以B为圆心,为半径的弧交于点D,则图中阴影部分图形的面积为___________.
15.如图,在扇形AOB中,OA=4,∠AOB=90°,点P是弧AB上的动点,连接OP,点C是线段OP的中点,连接BC并延长交OA于点D,则图中阴影部分面积最小值为___.
16.如图,等边△ABC边长为2,点D、E、F分别是AB、BC、AC的中点,分别以D、E、F为圆心,DE长为半径画弧,围成一个曲边三角形,则曲边三角形的面积为_______.
17.学校花园边墙上有一宽为的矩形门,量得门框对角线长为,为美化校园,现准备打掉地面上方的部分墙体,使其变为以为直径的圆弧形门,则要打掉墙体(阴影部分)的面积是 __.
三、解答题
18.如图,A、B、C三点在半径为1的上,四边形是菱形,求的长.
19.如图,O1、O2分别是两个扇形的圆心,求图中阴影部分的周长.
20.如图,已知△ABC内接于以AB为直径的⊙O中,P为AB延长线上一点,且∠PCB=∠A.
(1)求证:PC是⊙O的切线.
(2)若∠P=30°,AP=12,求的长.
21.如图,D是等边ABC内的一点,将线段AD绕点A顺时针旋转60°得到线段AE和扇形EAD,连接CD、BE、DE.
(1)若AD=1,求阴影部分的面积;(结果保留根号和π)
(2)若∠ADC=110°,求∠BED的度数.
22.如图,AB为⊙O的直径,射线AD交⊙O于点F,C为的中点,过点C作CE⊥AD,连接AC.
(1)求证:CE是⊙O的切线;
(2)若∠BAC=30°,AB=4,求阴影部分的面积.
试卷第1页,共3页
参考答案:
1.C
解:点经过的路线长为,故C正确.
故选:C.
2.C
解:在中,
,,.
,
,
将绕直角顶点逆时针旋转得△,
,
,
点转过的路径长为,
故选:C.
3.B
解:连接OA,OB,过点O作OH⊥AB于H则AH=BH.
由题意π AH2=27π,
∴AH2=27,
∵AH>0,
∴AH=,
∴sin∠AOH=,
∴∠AOH=60°,
∵OA=OB,OH⊥AB,
∴∠AOH=∠BOH=60°,
∴∠AOB=120°,
∴的长==4π(cm).
故选:B.
4.B
解:设圆锥的底面圆的半径为r,
根据题意可知:
AD=AE=4,∠DAE=45°,
∵圆锥底面圆的周长等于弧长,
∴,
∴,
∴该圆锥的底面圆的半径是,
故选:B.
5.D
解:甲的运动路线为一个半圆形的圆弧
甲的运动路径长
乙的运动路线为两个半圆形的圆弧,
乙的运动路径长
丙的运动路线为三个半圆形的圆弧,
丙的运动路径长
三人总路程相等,而速度也相等
三人同时到达
故选:D
6.D
解:如图,圆心滚动一周路径为长为,
∴滚动2020周后圆心所经过的路径长,
故选:D.
7.D
解:∵∠C=90°,CA=CB=4,
∴,,
∵三条弧所对的圆心角的和为180°,
三个扇形的面积和为,
∴三条弧与边AB所围成的阴影部分的面积=S△ABC﹣三个扇形的面积和=8﹣2π.
故选:D.
8.B
解:∵在⊙O上,∠ACB=40°,
∴∠AOB=2∠ACB=80°,
∴,
故选:B.
9.B
解:∵四边形ABCD是矩形,
∴∠B=90°,AD∥CB,
∵AB=1,AE=AD=2,
∴AE=2AB,
∴∠AEB=30°,
∴∠DAE=∠AEB=30°,
∴S阴==,
则图中空白部分的面积是
故选:B.
10.A
解:如图,连接BO,FO,OA.
由题意得,△OAF,△AOB都是等边三角形,
∴∠AOF=∠OAB=60°,
∴AB∥OF,
∴△OAB的面积=△ABF的面积,
∵六边形ABCDEF是正六边形,
∴AF=AB=OA=OB=,
∴阴影部分的面积=扇形OAB的面积×3=×3=.
故选:A.
11.B
解:如图,连接AC,连接AO并延长,交于点,连接DE
∵AB⊥CD,
∴∠CAB+∠ACD=90°,
∵AE是直径,
∴∠ADE=90°,
∴∠AED+∠EAD=90°,
又∵∠ACD=∠AED,
∴∠CAB=∠EAD,
∴CB=DE=2,
∴AE=,
将弓形BC旋转到弓形DE的位置,两块阴影部分面积之和为半圆面积减去△ADE的面积,
即.
故选B.
12.A
解:是正三角形,
,
的长为:,
“莱洛三角形”的周长.
故选:A.
13.24
解:的圆心角所对的弧长是,
由,
,
解得.
故答案为:24.
14.##
解:∵
∴
∴S扇形ACE=,
S扇形BCD=,
S△ABC=,
∴S阴影部分=S扇形ACE+S扇形BCD-S△ABC.
故答案为:.
15.
解:如图,OA=4,∠AOB=90°,点C是线段OP的中点,
OB=OP=4.
,
当OD的值最大时,阴影部分的面积最小.
,
当时,OD的值最大,
此时,,
,
,
,
阴影部分的面积的最小值是.
故答案为:.
16.
解:连接DE,DF,EF,
由题意得,,
∵点D、E、F分别是AB、BC、AC的中点,
∴,
∴是等边三角形,
∴,
∴曲边三角形的面积为:
=
=
故答案为:.
17.
解:过点作于,如图,
四边形是矩形,,,
,
∴在Rt△ABC中,,
∴∠ACB=30゜,
同理∠DBC=30゜
,
,
∴ ,
∵OA=OB,OM⊥BC,
∴M为BC的中点,
∵OA=OC
∴OM为△ABC的中位线
∴
,
,
故答案为:.
18.
解:连接OB.
∵四边形OABC是菱形,
∴OA=AB=OB=OC=BC,
∴△AOB,△BOC都是等边三角形,
∴∠AOB=∠BOC=60°,
∴∠AOC=120°,
∴的长=
19.(π+3)cm
解:∵⊙O1的半径为3cm,
∴⊙O2的半径是3=(cm),
∴图中阴影部分的周长是×2π×+3=(π+3)cm.
20.(1)见解析 (2)
(1)
证明:∵AB为直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
连接OC,可得OB=OC,
∴∠OCB=∠OBC,
又∵∠PCB=∠A,
∴∠PCB+∠OCB=90°,
∴∠OCP=90°,
∴PC是OO的切线;
(2)
解:由(1)得∠PCO=90°,
∵∠P=30°,
∴OC=OP,∠BOC=60°,
∵AO=BO,
∴OC=AP=×12=4,
∴LBC=.
21.(1) (2)
(1)
解:过点A作于点F,
绕点A旋转得到,
,
为等边三角形,
,
,
,
,
在中,,
,
,
;
(2)
解:为等边三角形,
,
,
,
即,
在与中,
,
,
,
为等边三角形,
,
,
.
22.(1)见解析 (2)
(1)
解:(1)连接BF,OC,
∵AB是⊙O的直径,
∴∠AFB=90°,即BF⊥AD,
∵CE⊥AD,
∴BF∥CE,
∵点C为劣弧的中点,
∴OC⊥BF,又BF∥CE,
∴OC⊥CE,
∵OC是⊙O的半径,
∴CE是⊙O的切线;
(2)
解:连接OF,CF,
∵OA=OC,
∴∠OCA=∠BAC=30°,
∴∠BOC=60°,
∵点C为劣弧的中点,
∴,
∴∠FOC=∠BOC=60°,
∵OF=OC,
∴△FOC为等边三角形,
∴∠OCF=∠COB=60°,
∴CF∥AB,
∴S△ACF=S△OCF,
∴阴影部分的面积等于S扇形COF,
∵AB=4,
∴FO=OC=OB=2,
∴S扇形FOC=,
即阴影部分的面积为.
答案第1页,共2页
一、单选题
1.如图,在扇形纸片中,,,在桌面内的直线上,现将此扇形沿按顺时针方向旋转(旋转过程中无滑动),当落在上时,停止旋转.则点所经过的路线长为( )
A. B. C. D.
2.如图,在中,,,.将绕直角顶点逆时针旋转得△;则点转过的路径长为( )
A. B. C. D.
3.已知水平放置半径为6cm的球形容器中装有溶液,容器内液面的面积为cm2,如图,是该球体的一个最大纵截面,则该截面中阴影部分的弧长为( )
A.cm B.cm C.cm D.cm
4.如图,正方形ABCD的边长为4,以点A为圆心,AD为半径,画圆弧DE得到扇形DAE(阴影部分,点E在对角线AC上),若扇形DAE正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A. B. C.2 D.4
5.如图,甲、乙、丙三人同时从点出发向点移动,甲的运动路线为一个半圆形的圆弧,乙的运动路线为两个半圆形的圆弧,丙的运动路线为三个半圆形的圆弧,若甲、乙、丙的运动速度相等,则谁先到达点( )
A.甲 B.乙 C.丙 D.三人同时到达
6.如图,将一个半径为1cm的半圆,在直线上从左往右作无滑动的滚动,则滚动2020周后圆心所经过的路径长为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A、B、C为圆心,以AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是( )
A.8﹣4π B.8﹣π C.16﹣2π D.8﹣2π
8.如图,点A、B、C是⊙O上的点,∠ACB=40°,⊙O的半径为3,则阴影部分的面积为( )
A.π B.2π C.3π D.4π
9.如图,在矩形ABCD中,AD=2,AB=1,以A为圆心,AD的长为半径画弧交BC于点E,则图中空白部分的面积是( )
A.1﹣ B.2﹣ C. D.2+
10.如图,在⊙O的内接正六边形ABCDEF中,AB=,则图中阴影部分的面积为( )
A. B. C. D.
11.如图,AB和CD是⊙O的两条互相垂直的弦,若AD=4,BC=2,则阴影部分的面积是( )
A.2π﹣1 B.π﹣4 C.5π﹣4 D.5π﹣8
12.如图,分别以等边△ABC的三个顶点为圆心,边长为半径画弧,得到的封闭图形是莱洛三角形.若AB=2,则此莱洛三角形的周长为( )
A.2π B.4π C.6 D.
二、填空题
13.75°的圆心角所对的弧长是10πcm,则此弧所在圆的半径是 _____cm.
14.如图,在中,,若以点A为圆心,半径的弧交于点E,以B为圆心,为半径的弧交于点D,则图中阴影部分图形的面积为___________.
15.如图,在扇形AOB中,OA=4,∠AOB=90°,点P是弧AB上的动点,连接OP,点C是线段OP的中点,连接BC并延长交OA于点D,则图中阴影部分面积最小值为___.
16.如图,等边△ABC边长为2,点D、E、F分别是AB、BC、AC的中点,分别以D、E、F为圆心,DE长为半径画弧,围成一个曲边三角形,则曲边三角形的面积为_______.
17.学校花园边墙上有一宽为的矩形门,量得门框对角线长为,为美化校园,现准备打掉地面上方的部分墙体,使其变为以为直径的圆弧形门,则要打掉墙体(阴影部分)的面积是 __.
三、解答题
18.如图,A、B、C三点在半径为1的上,四边形是菱形,求的长.
19.如图,O1、O2分别是两个扇形的圆心,求图中阴影部分的周长.
20.如图,已知△ABC内接于以AB为直径的⊙O中,P为AB延长线上一点,且∠PCB=∠A.
(1)求证:PC是⊙O的切线.
(2)若∠P=30°,AP=12,求的长.
21.如图,D是等边ABC内的一点,将线段AD绕点A顺时针旋转60°得到线段AE和扇形EAD,连接CD、BE、DE.
(1)若AD=1,求阴影部分的面积;(结果保留根号和π)
(2)若∠ADC=110°,求∠BED的度数.
22.如图,AB为⊙O的直径,射线AD交⊙O于点F,C为的中点,过点C作CE⊥AD,连接AC.
(1)求证:CE是⊙O的切线;
(2)若∠BAC=30°,AB=4,求阴影部分的面积.
试卷第1页,共3页
参考答案:
1.C
解:点经过的路线长为,故C正确.
故选:C.
2.C
解:在中,
,,.
,
,
将绕直角顶点逆时针旋转得△,
,
,
点转过的路径长为,
故选:C.
3.B
解:连接OA,OB,过点O作OH⊥AB于H则AH=BH.
由题意π AH2=27π,
∴AH2=27,
∵AH>0,
∴AH=,
∴sin∠AOH=,
∴∠AOH=60°,
∵OA=OB,OH⊥AB,
∴∠AOH=∠BOH=60°,
∴∠AOB=120°,
∴的长==4π(cm).
故选:B.
4.B
解:设圆锥的底面圆的半径为r,
根据题意可知:
AD=AE=4,∠DAE=45°,
∵圆锥底面圆的周长等于弧长,
∴,
∴,
∴该圆锥的底面圆的半径是,
故选:B.
5.D
解:甲的运动路线为一个半圆形的圆弧
甲的运动路径长
乙的运动路线为两个半圆形的圆弧,
乙的运动路径长
丙的运动路线为三个半圆形的圆弧,
丙的运动路径长
三人总路程相等,而速度也相等
三人同时到达
故选:D
6.D
解:如图,圆心滚动一周路径为长为,
∴滚动2020周后圆心所经过的路径长,
故选:D.
7.D
解:∵∠C=90°,CA=CB=4,
∴,,
∵三条弧所对的圆心角的和为180°,
三个扇形的面积和为,
∴三条弧与边AB所围成的阴影部分的面积=S△ABC﹣三个扇形的面积和=8﹣2π.
故选:D.
8.B
解:∵在⊙O上,∠ACB=40°,
∴∠AOB=2∠ACB=80°,
∴,
故选:B.
9.B
解:∵四边形ABCD是矩形,
∴∠B=90°,AD∥CB,
∵AB=1,AE=AD=2,
∴AE=2AB,
∴∠AEB=30°,
∴∠DAE=∠AEB=30°,
∴S阴==,
则图中空白部分的面积是
故选:B.
10.A
解:如图,连接BO,FO,OA.
由题意得,△OAF,△AOB都是等边三角形,
∴∠AOF=∠OAB=60°,
∴AB∥OF,
∴△OAB的面积=△ABF的面积,
∵六边形ABCDEF是正六边形,
∴AF=AB=OA=OB=,
∴阴影部分的面积=扇形OAB的面积×3=×3=.
故选:A.
11.B
解:如图,连接AC,连接AO并延长,交于点,连接DE
∵AB⊥CD,
∴∠CAB+∠ACD=90°,
∵AE是直径,
∴∠ADE=90°,
∴∠AED+∠EAD=90°,
又∵∠ACD=∠AED,
∴∠CAB=∠EAD,
∴CB=DE=2,
∴AE=,
将弓形BC旋转到弓形DE的位置,两块阴影部分面积之和为半圆面积减去△ADE的面积,
即.
故选B.
12.A
解:是正三角形,
,
的长为:,
“莱洛三角形”的周长.
故选:A.
13.24
解:的圆心角所对的弧长是,
由,
,
解得.
故答案为:24.
14.##
解:∵
∴
∴S扇形ACE=,
S扇形BCD=,
S△ABC=,
∴S阴影部分=S扇形ACE+S扇形BCD-S△ABC.
故答案为:.
15.
解:如图,OA=4,∠AOB=90°,点C是线段OP的中点,
OB=OP=4.
,
当OD的值最大时,阴影部分的面积最小.
,
当时,OD的值最大,
此时,,
,
,
,
阴影部分的面积的最小值是.
故答案为:.
16.
解:连接DE,DF,EF,
由题意得,,
∵点D、E、F分别是AB、BC、AC的中点,
∴,
∴是等边三角形,
∴,
∴曲边三角形的面积为:
=
=
故答案为:.
17.
解:过点作于,如图,
四边形是矩形,,,
,
∴在Rt△ABC中,,
∴∠ACB=30゜,
同理∠DBC=30゜
,
,
∴ ,
∵OA=OB,OM⊥BC,
∴M为BC的中点,
∵OA=OC
∴OM为△ABC的中位线
∴
,
,
故答案为:.
18.
解:连接OB.
∵四边形OABC是菱形,
∴OA=AB=OB=OC=BC,
∴△AOB,△BOC都是等边三角形,
∴∠AOB=∠BOC=60°,
∴∠AOC=120°,
∴的长=
19.(π+3)cm
解:∵⊙O1的半径为3cm,
∴⊙O2的半径是3=(cm),
∴图中阴影部分的周长是×2π×+3=(π+3)cm.
20.(1)见解析 (2)
(1)
证明:∵AB为直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
连接OC,可得OB=OC,
∴∠OCB=∠OBC,
又∵∠PCB=∠A,
∴∠PCB+∠OCB=90°,
∴∠OCP=90°,
∴PC是OO的切线;
(2)
解:由(1)得∠PCO=90°,
∵∠P=30°,
∴OC=OP,∠BOC=60°,
∵AO=BO,
∴OC=AP=×12=4,
∴LBC=.
21.(1) (2)
(1)
解:过点A作于点F,
绕点A旋转得到,
,
为等边三角形,
,
,
,
,
在中,,
,
,
;
(2)
解:为等边三角形,
,
,
,
即,
在与中,
,
,
,
为等边三角形,
,
,
.
22.(1)见解析 (2)
(1)
解:(1)连接BF,OC,
∵AB是⊙O的直径,
∴∠AFB=90°,即BF⊥AD,
∵CE⊥AD,
∴BF∥CE,
∵点C为劣弧的中点,
∴OC⊥BF,又BF∥CE,
∴OC⊥CE,
∵OC是⊙O的半径,
∴CE是⊙O的切线;
(2)
解:连接OF,CF,
∵OA=OC,
∴∠OCA=∠BAC=30°,
∴∠BOC=60°,
∵点C为劣弧的中点,
∴,
∴∠FOC=∠BOC=60°,
∵OF=OC,
∴△FOC为等边三角形,
∴∠OCF=∠COB=60°,
∴CF∥AB,
∴S△ACF=S△OCF,
∴阴影部分的面积等于S扇形COF,
∵AB=4,
∴FO=OC=OB=2,
∴S扇形FOC=,
即阴影部分的面积为.
答案第1页,共2页
