2021-2022学年人教版下册八年级数学18.2.1矩形的性质 基础练习(word版 含解析)
文档属性
| 名称 | 2021-2022学年人教版下册八年级数学18.2.1矩形的性质 基础练习(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 127.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 09:45:40 | ||
图片预览



文档简介
18.2.1 矩形的性质 基础练习-2021-2022学年人教版下册八年级数学
一、选择题
如下图,矩形中,,,则的长是
A. B. C. D.
若矩形的邻边长分别是,,则的长是
A. B. C. D.
若矩形对角线相交所成的钝角为,短边长为,则对角线的长为
A. B. C. D.
如图,矩形的对角线,相交于点,是的中点,连接若,,则对角线的长为
A. B. C. D.
如图,在矩形中,,,则的长是
A. B. C. D.
如图所示,点是矩形对角线的中点,交于点若,,则周长为
A. B. C. D.
二、填空题
如图,在矩形中,,对角线,相交于点,垂直平分于点,则的长为________.
如图,在矩形中,,对角线、相交于点,垂直平分于点,则的长为____________.
如下图,延长矩形的边至点,使,连接,若,则__________
如图,在矩形中,是边上一点,,,是边的中点,,则 ______ .
三、解答题
如图,已知矩形,过点作交的延长线于点求证:.
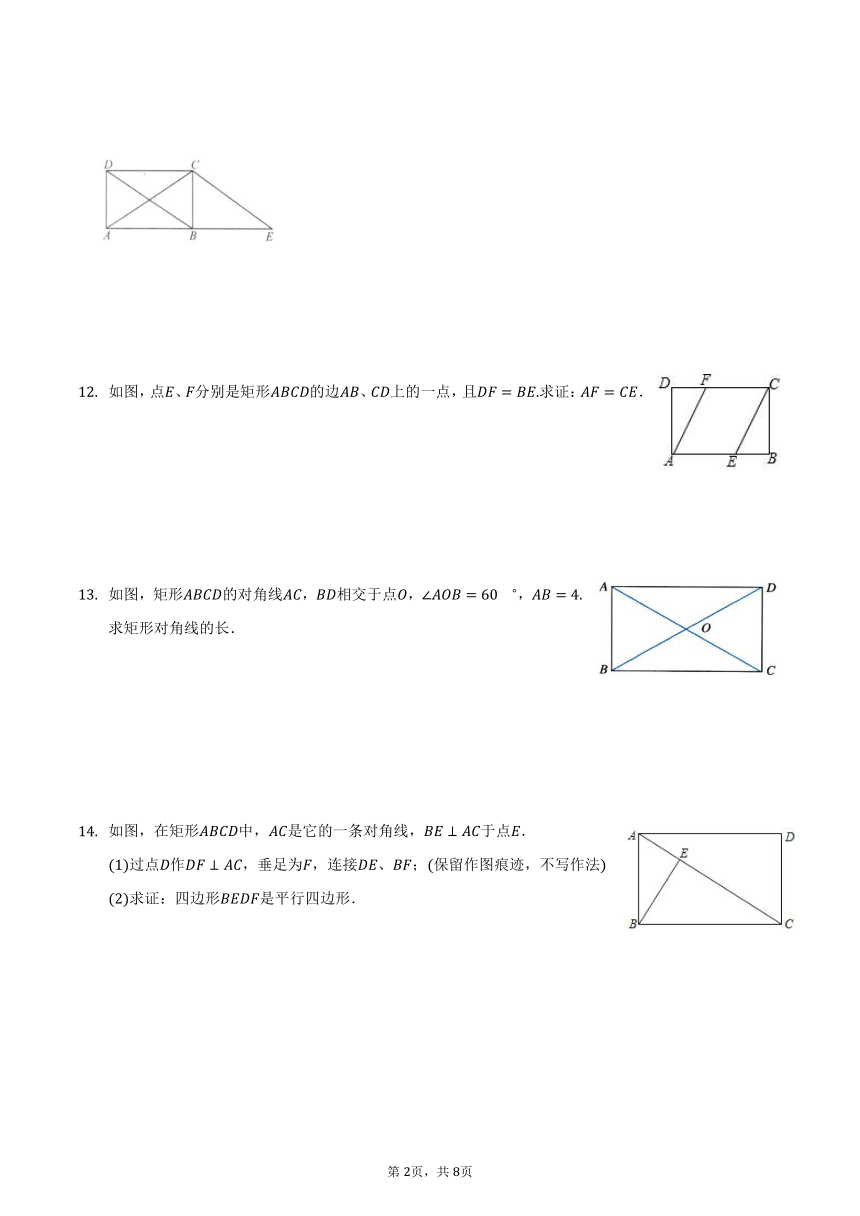
如图,点、分别是矩形的边、上的一点,且求证:.
如图,矩形的对角线,相交于点,,求矩形对角线的长.
如图,在矩形中,是它的一条对角线,于点.
过点作,垂足为,连接、;保留作图痕迹,不写作法
求证:四边形是平行四边形.
参考答案与解析
1.【答案】
【解析】
【分析】
本题考查了矩形的性质和等边三角形的判定,先由矩形的性质及等边三角形的判定定理得出为等边三角形,则可得出的长,然后根据,可求得答案.
【解答】
解:四边形是矩形,
,,
,
为等边三角形,
,
,
.
故选D.
2.【答案】
3.【答案】
4.【答案】
5.【答案】
【解析】解:四边形是矩形,
,
,,
,
故选:.
根据矩形的性质直接利用勾股定理求得答案即可.
本题考查了矩形的性质,解题的关键是能够利用矩形的性质得到直角三角形,难度不大.
6.【答案】
【解析】解:点是矩形对角线的中点,,
,点为中点.
在中,利用勾股定理求得.
在中,利用勾股定理求得.
.
周长为.
故选:.
易知是中位线,则,在中,利用勾股定理求得,在中,利用勾股定理求得,根据矩形性质可求,从而求出周长.
本题主要考查了矩形的性质、以及勾股定理和中位线的性质,解题的技巧是把所求三角形的三条线段分别放在不同的三角形中求解长度.
7.【答案】
8.【答案】
【解析】解:四边形是矩形,
,,,
,
垂直平分,
,
,
,
,
故答案为:.
由矩形的性质和线段垂直平分线的性质证出,得出,由勾股定理求出即可.
此题考查了矩形的性质、等边三角形的判定与性质、线段垂直平分线的性质、勾股定理;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.
9.【答案】
【解析】
【分析】
本题主要考查矩形性质,熟练掌握矩形对角线相等且互相平分、对边平行是解题关键.
连接,由矩形性质可得、,知,而,可得度数.
【解答】
解:连接,
四边形是矩形,
,,且,
,
又,
,
,
,
.
故答案为:
10.【答案】
【解析】解:,是边的中点,,
,
,
,
又四边形是矩形,
,,
,
在中,
,
故答案为:.
先利用直角三角形斜边上的中线等于斜边的一半,求出长,再根据矩形的性质得出,,然后解直角三角形即可.
本题考查了矩形的性质直角三角形斜边上的中线以及解直角三角形,关键是利用直角三角形斜边上的中线求出的长.
11.【答案】证明:四边形是矩形,
,.
又,
四边形是平行四边形.
.
.
【解析】本题主要考查矩形的性质、平行四边形的判定和性质,掌握相关判定和性质是解题的关键.
先由矩形的性质得到,,再结合已知条件证明四边形是平行四边形,得到,进而可证明出结论.
12.【答案】证明:四边形是矩形,
,,
在和中,
≌,
.
【解析】本题考查了矩形的性质、全等三角形的判定与性质;熟练掌握矩形的性质,证明三角形全等是解题的关键.
由证明≌,即可得出.
13.【答案】解:四边形是矩形,
与相等且互相平分.
.
又,
是等边三角形.
.
.
【解析】见答案
14.【答案】解:如图,即为所求:
四边形为矩形,
,,
,
,,
,,
,
≌,
,
而,
四边形是平行四边形.
【解析】利用基本作图求解;
先根据矩形的性质得到,,再证明,接着证明≌,从而得到,然后根据平行四边形的判定方法得到结论.
本题考查了作图基本作图:熟练掌握种基本作图作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线也考查了全等三角形的判定与性质和平行四边形的判定.
第2页,共2页
一、选择题
如下图,矩形中,,,则的长是
A. B. C. D.
若矩形的邻边长分别是,,则的长是
A. B. C. D.
若矩形对角线相交所成的钝角为,短边长为,则对角线的长为
A. B. C. D.
如图,矩形的对角线,相交于点,是的中点,连接若,,则对角线的长为
A. B. C. D.
如图,在矩形中,,,则的长是
A. B. C. D.
如图所示,点是矩形对角线的中点,交于点若,,则周长为
A. B. C. D.
二、填空题
如图,在矩形中,,对角线,相交于点,垂直平分于点,则的长为________.
如图,在矩形中,,对角线、相交于点,垂直平分于点,则的长为____________.
如下图,延长矩形的边至点,使,连接,若,则__________
如图,在矩形中,是边上一点,,,是边的中点,,则 ______ .
三、解答题
如图,已知矩形,过点作交的延长线于点求证:.
如图,点、分别是矩形的边、上的一点,且求证:.
如图,矩形的对角线,相交于点,,求矩形对角线的长.
如图,在矩形中,是它的一条对角线,于点.
过点作,垂足为,连接、;保留作图痕迹,不写作法
求证:四边形是平行四边形.
参考答案与解析
1.【答案】
【解析】
【分析】
本题考查了矩形的性质和等边三角形的判定,先由矩形的性质及等边三角形的判定定理得出为等边三角形,则可得出的长,然后根据,可求得答案.
【解答】
解:四边形是矩形,
,,
,
为等边三角形,
,
,
.
故选D.
2.【答案】
3.【答案】
4.【答案】
5.【答案】
【解析】解:四边形是矩形,
,
,,
,
故选:.
根据矩形的性质直接利用勾股定理求得答案即可.
本题考查了矩形的性质,解题的关键是能够利用矩形的性质得到直角三角形,难度不大.
6.【答案】
【解析】解:点是矩形对角线的中点,,
,点为中点.
在中,利用勾股定理求得.
在中,利用勾股定理求得.
.
周长为.
故选:.
易知是中位线,则,在中,利用勾股定理求得,在中,利用勾股定理求得,根据矩形性质可求,从而求出周长.
本题主要考查了矩形的性质、以及勾股定理和中位线的性质,解题的技巧是把所求三角形的三条线段分别放在不同的三角形中求解长度.
7.【答案】
8.【答案】
【解析】解:四边形是矩形,
,,,
,
垂直平分,
,
,
,
,
故答案为:.
由矩形的性质和线段垂直平分线的性质证出,得出,由勾股定理求出即可.
此题考查了矩形的性质、等边三角形的判定与性质、线段垂直平分线的性质、勾股定理;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.
9.【答案】
【解析】
【分析】
本题主要考查矩形性质,熟练掌握矩形对角线相等且互相平分、对边平行是解题关键.
连接,由矩形性质可得、,知,而,可得度数.
【解答】
解:连接,
四边形是矩形,
,,且,
,
又,
,
,
,
.
故答案为:
10.【答案】
【解析】解:,是边的中点,,
,
,
,
又四边形是矩形,
,,
,
在中,
,
故答案为:.
先利用直角三角形斜边上的中线等于斜边的一半,求出长,再根据矩形的性质得出,,然后解直角三角形即可.
本题考查了矩形的性质直角三角形斜边上的中线以及解直角三角形,关键是利用直角三角形斜边上的中线求出的长.
11.【答案】证明:四边形是矩形,
,.
又,
四边形是平行四边形.
.
.
【解析】本题主要考查矩形的性质、平行四边形的判定和性质,掌握相关判定和性质是解题的关键.
先由矩形的性质得到,,再结合已知条件证明四边形是平行四边形,得到,进而可证明出结论.
12.【答案】证明:四边形是矩形,
,,
在和中,
≌,
.
【解析】本题考查了矩形的性质、全等三角形的判定与性质;熟练掌握矩形的性质,证明三角形全等是解题的关键.
由证明≌,即可得出.
13.【答案】解:四边形是矩形,
与相等且互相平分.
.
又,
是等边三角形.
.
.
【解析】见答案
14.【答案】解:如图,即为所求:
四边形为矩形,
,,
,
,,
,,
,
≌,
,
而,
四边形是平行四边形.
【解析】利用基本作图求解;
先根据矩形的性质得到,,再证明,接着证明≌,从而得到,然后根据平行四边形的判定方法得到结论.
本题考查了作图基本作图:熟练掌握种基本作图作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线也考查了全等三角形的判定与性质和平行四边形的判定.
第2页,共2页
