2021-2022学年湘教版八年级数学下册 2.5矩形 同步达标测试题(word版含解析)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学下册 2.5矩形 同步达标测试题(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 305.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 00:00:00 | ||
图片预览

文档简介
2021-2022学年湘教版八年级数学下册《2-5矩形》同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量其中三个角是否都为直角
C.测量对角线是否相等
D.测量两组对边是否分别相等
2.如图,在矩形ABCD中,AB=2,BC=4,对角线AC,BD相交于点O,OE⊥AC交BC于点F,EF⊥BD于点F,则OE+EF的值为( )
A. B.2 C. D.2
3.如图,四边形ABCD是平行四边形,两条对角线交于点O,下列条件中,不能判定平行四边形ABCD为矩形的是( )
A.∠ABC=∠BCD B.∠ABC=∠ADC C.AO=BO D.AO=DO
4.如图,矩形ABCD中,AB=8cm,AD=6cm,EF是对角线BD的垂直平分线,则EF的长为( )
A.cm B.cm C.cm D.8cm
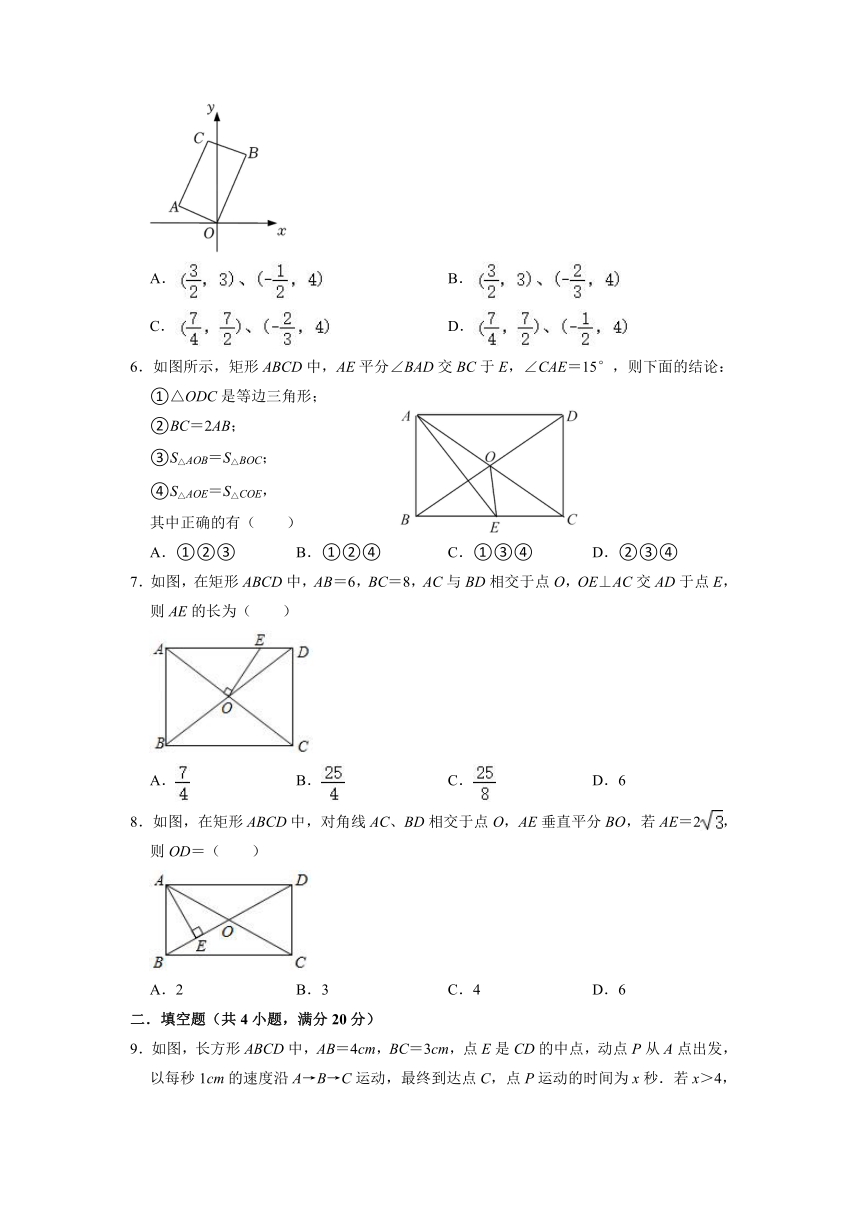
5.如图,已知矩形AOBC的顶点O在坐标原点,点A的坐标是(﹣2,1),点C的纵坐标是4,则B,C两点的坐标分别是( )
A. B.
C. D.
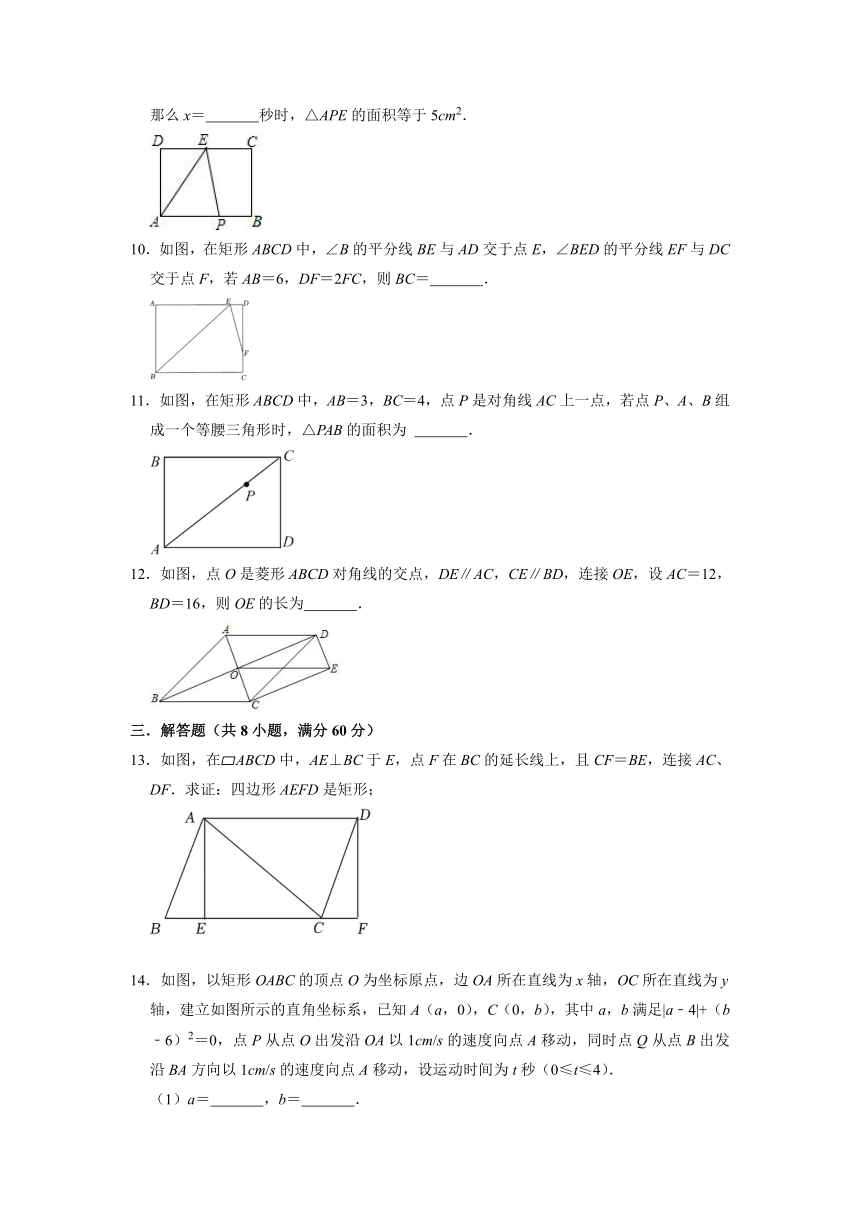
6.如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:
①△ODC是等边三角形;
②BC=2AB;
③S△AOB=S△BOC;
④S△AOE=S△COE,
其中正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
7.如图,在矩形ABCD中,AB=6,BC=8,AC与BD相交于点O,OE⊥AC交AD于点E,则AE的长为( )
A. B. C. D.6
8.如图,在矩形ABCD中,对角线AC、BD相交于点O,AE垂直平分BO,若AE=2,则OD=( )
A.2 B.3 C.4 D.6
二.填空题(共4小题,满分20分)
9.如图,长方形ABCD中,AB=4cm,BC=3cm,点E是CD的中点,动点P从A点出发,以每秒1cm的速度沿A→B→C运动,最终到达点C,点P运动的时间为x秒.若x>4,那么x= 秒时,△APE的面积等于5cm2.
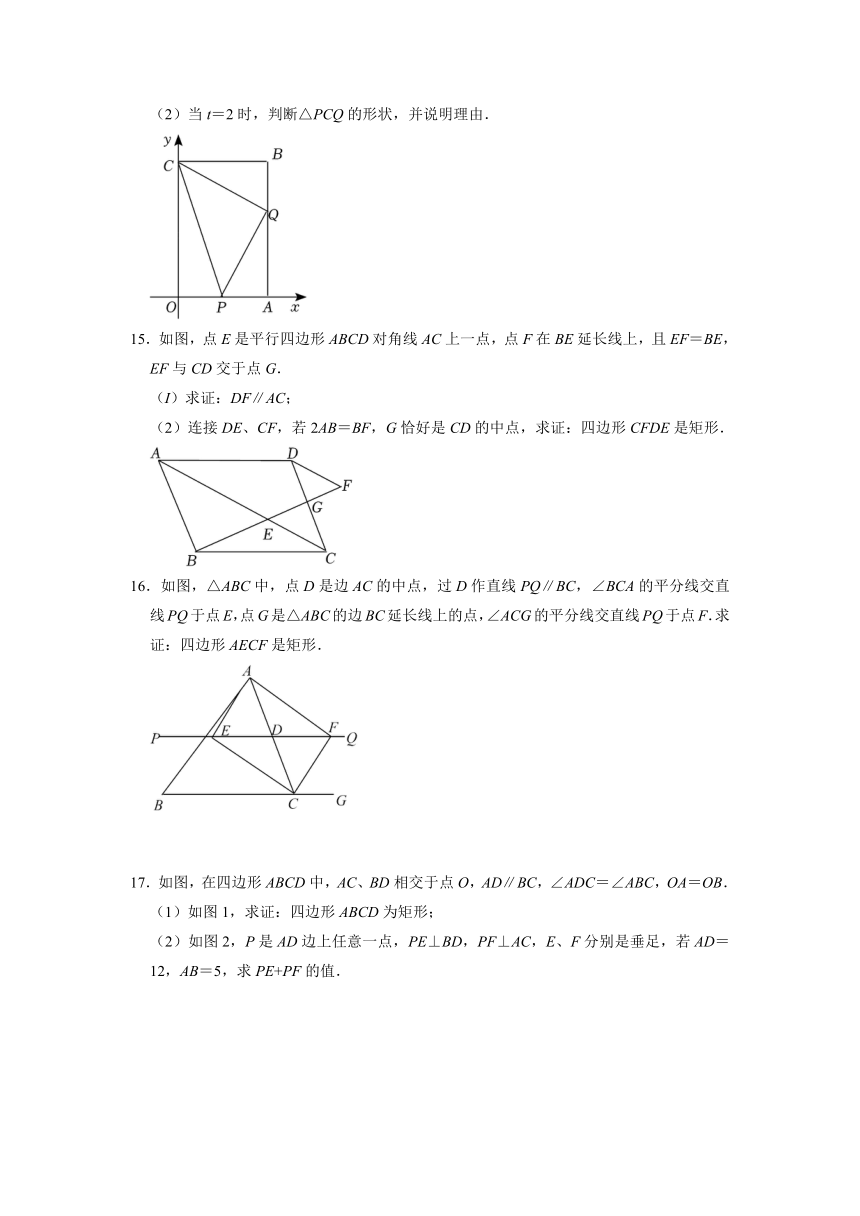
10.如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=6,DF=2FC,则BC= .
11.如图,在矩形ABCD中,AB=3,BC=4,点P是对角线AC上一点,若点P、A、B组成一个等腰三角形时,△PAB的面积为 .
12.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为 .
三.解答题(共8小题,满分60分)
13.如图,在 ABCD中,AE⊥BC于E,点F在BC的延长线上,且CF=BE,连接AC、DF.求证:四边形AEFD是矩形;
14.如图,以矩形OABC的顶点O为坐标原点,边OA所在直线为x轴,OC所在直线为y轴,建立如图所示的直角坐标系,已知A(a,0),C(0,b),其中a,b满足|a﹣4|+(b﹣6)2=0,点P从点O出发沿OA以1cm/s的速度向点A移动,同时点Q从点B出发沿BA方向以1cm/s的速度向点A移动,设运动时间为t秒(0≤t≤4).
(1)a= ,b= .
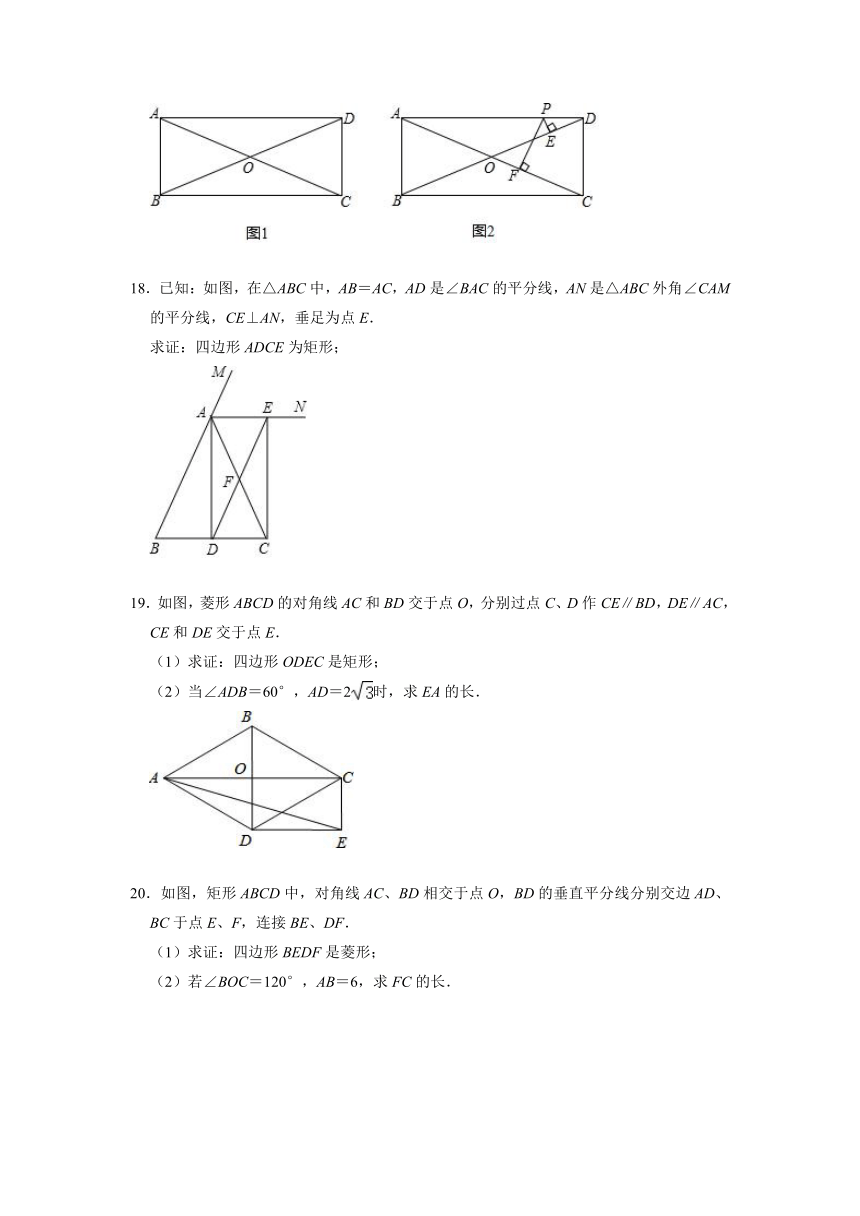
(2)当t=2时,判断△PCQ的形状,并说明理由.
15.如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G.
(I)求证:DF∥AC;
(2)连接DE、CF,若2AB=BF,G恰好是CD的中点,求证:四边形CFDE是矩形.
16.如图,△ABC中,点D是边AC的中点,过D作直线PQ∥BC,∠BCA的平分线交直线PQ于点E,点G是△ABC的边BC延长线上的点,∠ACG的平分线交直线PQ于点F.求证:四边形AECF是矩形.
17.如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.
(1)如图1,求证:四边形ABCD为矩形;
(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF的值.
18.已知:如图,在△ABC中,AB=AC,AD是∠BAC的平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
求证:四边形ADCE为矩形;
19.如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2时,求EA的长.
20.如图,矩形ABCD中,对角线AC、BD相交于点O,BD的垂直平分线分别交边AD、BC于点E、F,连接BE、DF.
(1)求证:四边形BEDF是菱形;
(2)若∠BOC=120°,AB=6,求FC的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:A、对角线是否相互平分,能判定平行四边形;
B、其中四边形中三个角都为直角,能判定矩形;
C、对角线相等的四边形不一定是矩形,不能判定形状;
D、两组对边是否分别相等,能判定平行四边形.
故选:B.
2.解:∵AB=2,BC=4,
∴矩形ABCD的面积为8,AC===2,
∴BO=CO=AC=,
∵对角线AC,BD交于点O,
∴△BOC的面积为2,
∵EO⊥AO,EF⊥DO,
∴S△BOC=S△BOE+S△COE,
2=CO×EO+BO×EF,
∴2=××EO+×EF,
∴(EO+EF)=4,
∴EO+EF=,
故选:A.
3.解:A、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC=∠BCD,
∴∠ABC=90°,
∴平行四边形ABCD为矩形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∴不能判定平行四边形ABCD为矩形,故选项B符合题意;
C、∵四边形ABCD是平行四边形,
∴AO=CO=AC,BO=DO=BD,
∵AO=BO,
∴AC=BD,
∴平行四边形ABCD为矩形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,
∴AO=CO=AC,BO=DO=BD,
∵AO=DO,
∴AC=BD,
∴平行四边形ABCD为矩形,故选项D不符合题意;
故选:B.
4.解:∵EF是BD的垂直平分线,
∴OB=OD,
∵∠OBF=∠ODE,∠BOF=∠DOE,
∴△BOF≌△DOE,则OE=OF,
∵∠OBF=∠ABD,
∵BD==10cm,
∴BO=5cm,
∴FO=5×cm=cm,
∴EF=2FO=cm.
故选:C.
5.解:如图,过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,延长CA交x轴于点H,
∵四边形AOBC是矩形,
∴AC∥OB,AC=OB,
∴∠CAF=∠BOE=∠CHO,
在△ACF和△OBE中,
,
∴△CAF≌△BOE(AAS),
∴BE=CF=4﹣1=3,
∵∠AOD+∠BOE=∠BOE+∠OBE=90°,
∴∠AOD=∠OBE,
∵∠ADO=∠OEB=90°,
∴OE=,即点B(,3),
∴AF=OE=,
∴点C的横坐标为:﹣(2﹣)=﹣,
∴点C(﹣,4).
故选:A.
6.解:∵四边形ABCD是矩形,
∴AD∥BC,∠BAD=∠ABC=∠ADC=90°,OA=OC,OD=OB,AC=BD,
∴OA=OD=OC=OB,
∵AE平分∠BAD,
∴∠DAE=45°,
∵∠CAE=15°,
∴∠DAC=45°﹣15°=30°,
∴∠ACD=90°﹣∠DAC=90°﹣30°=60°,
∵OD=OC,
∴△ODC是等边三角形,故①正确;
∵AD∥BC,
∴∠ACB=∠DAC=30°,
∵∠ABC=90°,
∴AC=2AB,
而AC>BC,
∴2AB>BC,故②错误;
∵OA=OC,
∴S△AOB=S△BOC、S△AOE=S△COE,故③、④正确;
故选:C.
7.解:如图,连接CE,
∵矩形ABCD中,AB=6,BC=8,
∴AD=BC=8,CD=AB=6,OA=OC,
∵OE⊥AC,
∴OE垂直平分AC,
∴AE=CE,
设AE=CE=x,则DE=8﹣x,
在Rt△CDE中,CD2+DE2=CE2,
即62+(8﹣x)2=x2,
解得x=,
即AE的长为.
故选:B.
8.解:∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵AE垂直平分OB,
∴AB=AO,
∴OA=AB=OB,
∵AE=2,
∴OE=2,
∴OD=OB=2OE=4;
故选:C.
二.填空题(共4小题,满分20分)
9.解:∵x>4,
∴点P在BC上时,
∵△APE的面积等于5cm2,
∴S长方形ABCD﹣S△CPE﹣S△ADE﹣S△ABP=5,
∴3×4﹣(3+4﹣x)×2﹣×2×3﹣×4×(x﹣4)=5,
∴x=5;
∴x=5秒时,△APE的面积等于5cm2.
故答案为:5.
10.解:延长EF和BC,交于点G
∵矩形ABCD中,∠B的角平分线BE与AD交于点E,
∴∠ABE=∠AEB=45°,
∴AB=AE=6,
∴直角三角形ABE中,BE==6,
又∵∠BED的角平分线EF与DC交于点F,
∴∠BEG=∠DEF,
∵AD∥BC,
∴∠G=∠DEF,
∴∠BEG=∠G,
∴BG=BE=6,
∵∠G=∠DEF,∠EFD=∠GFC,
设CG=x,DE=2x,则AD=6+2x=BC,
∵BG=BC+CG,
∴6=6+2x+x
解得x=2﹣2,
∴BC=6+2(2﹣2)=4+2,
故答案为:4+2.
11.解:∵四边形ABCD是矩形,
∴∠ABC=90°,
由勾股定理得:AC===5,
有三种情况:
①当AB=BP=3时,如图1,过B作BM⊥AC于M,
∵S△ABC=,
∴=,
解得:BM=,
∵AB=BP=3,BM⊥AC,
∴AM=PM==,
∴AP=AM+PM=,
∴△PAB的面积S==××=;
②当AB=AP=3时,如图2,
∵BM=,
∴△PAB的面积S=
=
=;
③作AB的垂直平分线NQ,交AB于N,交AC于P,如图3,则AP=BP,BN=AN==,
∵四边形ABCD是矩形,NQ⊥AB,
∴PN∥BC,
∵AN=BN,
∴AP=CP,
∴PN=BC==2,
∴△PAB的面积S=
=2
=3;
即△PAB的面积为或或3,
故答案为:或或3.
12.解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故答案为:10.
三.解答题(共8小题,满分60分)
13.(1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即 EF=BC.
∵在 ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形;14.(1)解:∵|a﹣4|+(b﹣6)2=0,
∵|a﹣4|≥0,(b﹣6)2≥0,
∴a﹣4=0,b﹣6=0,
∴a=4,b=6;
故答案为:4;6;
(2)当t=2时,△PCQ是等腰直角三角形,理由如下:
设运动时间为t秒(0≤t≤4),
∴OP=t,AQ=6﹣t,
当t=2时,OP=2,AQ=6﹣2=4,
∴AP=OA﹣OP=4﹣2=2,
∵四边形OABC是矩形,
∴∠COA=∠OAB=∠B=90°,
在Rt△COA中,PC=,
在Rt△APQ中,PQ=,
在Rt△CBQ中,CQ=,
∴CQ=PQ,PC2=PQ2+CQ2,
∴△CPQ是等腰直角三角形.
15.(1)证明:连接BD,交AC于点O,如图所示:
∵四边形ABCD是平行四边形,
∴BO=DO,
∵BE=EF,
∴OE是△BDF的中位线,
∴OE∥DF,
即DF∥AC;
(2)证明:如图所示:
由(1)得:DF∥AC,
∴∠DFG=∠CEG,∠GDF=∠GCE,
∵G是CD的中点,
∴DG=CG,
在△DFG和△CEG中,
,
∴△DFG≌△CEG(AAS),
∴FG=EG,
∴四边形CFDE是平行四边形,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵2AB=BF,
∴2CD=BF,
又∵EF=BE,
∴CD=EF,
∴平行四边形CFDE是矩形.
16.证明:∵PQ∥BC,
∴∠DEC=∠BCE,∠DFC=∠GCF,
∵CE平分∠BCA,CF平分∠ACG,
∴∠BCE=∠DCE,∠DCF=∠GCF,
∴∠DEC=∠DCE,∠DFC=∠DCF,
∴DE=DC,DF=DC,
∴DE=DF,
∵点D是边AC的中点,
∴AD=CD,
∴四边形AECF是平行四边形,
∵∠BCA+∠ACG=180°,
∴∠ECF=∠DCE+∠DCF=×180°=90°,
∴平行四边形AECF是矩形.
17.证明:(1)∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形;
(2)如图,连接OP,
∵AD=12,AB=5,
∴BD===13,
∴BO=OD=AO=CO=,
∵S△AOD=S矩形ABCD=×12×5=15,
∴S△AOP+S△POD=15,
∴××FP+××EP=15,
∴PE+PF=.
18.证明:∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,∠BAD=∠CAD.
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN.
∴∠DAE=90°,
∵CE⊥AN,
∴∠AEC=90°.
∴四边形ADCE为矩形.
19.(1)证明:∵CE∥BD,DE∥AC,
∴四边形ODEC是平行四边形.
又∵菱形ABCD,
∴AC⊥BD,∴∠DOC=90°.
∴四边形ODEC是矩形.
(2)解:
20.(1)证明:∵EF垂直平分BD,
∴EB=ED,FB=FD,BO=DO,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠OBF=∠ODE,
∵∠DOE=∠BOF,
∴△EOD≌△FOB(AAS),
∴DE=BF,
∴EB=ED=FB=FD,
∴四边形BEDF是菱形;
(2)解:∵四边形ABCD是矩形,
∴OB=OC,CD=AB=6,
∴∠OBC=∠OCB,
∵∠BOC=120°,
∴∠OBC=∠OCB=30°,
∵四边形EBFD为菱形,
∴FB=FD,
∴∠FBD=∠FDB=30°,
∴∠DFC=60°,
∴∠FDC=30°,
设CF=x,则FD=2x,
根据勾股定理得:(2x)2﹣x2=62,
解得:x=2,
∴FC的长为2.
一.选择题(共8小题,满分40分)
1.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量其中三个角是否都为直角
C.测量对角线是否相等
D.测量两组对边是否分别相等
2.如图,在矩形ABCD中,AB=2,BC=4,对角线AC,BD相交于点O,OE⊥AC交BC于点F,EF⊥BD于点F,则OE+EF的值为( )
A. B.2 C. D.2
3.如图,四边形ABCD是平行四边形,两条对角线交于点O,下列条件中,不能判定平行四边形ABCD为矩形的是( )
A.∠ABC=∠BCD B.∠ABC=∠ADC C.AO=BO D.AO=DO
4.如图,矩形ABCD中,AB=8cm,AD=6cm,EF是对角线BD的垂直平分线,则EF的长为( )
A.cm B.cm C.cm D.8cm
5.如图,已知矩形AOBC的顶点O在坐标原点,点A的坐标是(﹣2,1),点C的纵坐标是4,则B,C两点的坐标分别是( )
A. B.
C. D.
6.如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:
①△ODC是等边三角形;
②BC=2AB;
③S△AOB=S△BOC;
④S△AOE=S△COE,
其中正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
7.如图,在矩形ABCD中,AB=6,BC=8,AC与BD相交于点O,OE⊥AC交AD于点E,则AE的长为( )
A. B. C. D.6
8.如图,在矩形ABCD中,对角线AC、BD相交于点O,AE垂直平分BO,若AE=2,则OD=( )
A.2 B.3 C.4 D.6
二.填空题(共4小题,满分20分)
9.如图,长方形ABCD中,AB=4cm,BC=3cm,点E是CD的中点,动点P从A点出发,以每秒1cm的速度沿A→B→C运动,最终到达点C,点P运动的时间为x秒.若x>4,那么x= 秒时,△APE的面积等于5cm2.
10.如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=6,DF=2FC,则BC= .
11.如图,在矩形ABCD中,AB=3,BC=4,点P是对角线AC上一点,若点P、A、B组成一个等腰三角形时,△PAB的面积为 .
12.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为 .
三.解答题(共8小题,满分60分)
13.如图,在 ABCD中,AE⊥BC于E,点F在BC的延长线上,且CF=BE,连接AC、DF.求证:四边形AEFD是矩形;
14.如图,以矩形OABC的顶点O为坐标原点,边OA所在直线为x轴,OC所在直线为y轴,建立如图所示的直角坐标系,已知A(a,0),C(0,b),其中a,b满足|a﹣4|+(b﹣6)2=0,点P从点O出发沿OA以1cm/s的速度向点A移动,同时点Q从点B出发沿BA方向以1cm/s的速度向点A移动,设运动时间为t秒(0≤t≤4).
(1)a= ,b= .
(2)当t=2时,判断△PCQ的形状,并说明理由.
15.如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G.
(I)求证:DF∥AC;
(2)连接DE、CF,若2AB=BF,G恰好是CD的中点,求证:四边形CFDE是矩形.
16.如图,△ABC中,点D是边AC的中点,过D作直线PQ∥BC,∠BCA的平分线交直线PQ于点E,点G是△ABC的边BC延长线上的点,∠ACG的平分线交直线PQ于点F.求证:四边形AECF是矩形.
17.如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.
(1)如图1,求证:四边形ABCD为矩形;
(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF的值.
18.已知:如图,在△ABC中,AB=AC,AD是∠BAC的平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
求证:四边形ADCE为矩形;
19.如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2时,求EA的长.
20.如图,矩形ABCD中,对角线AC、BD相交于点O,BD的垂直平分线分别交边AD、BC于点E、F,连接BE、DF.
(1)求证:四边形BEDF是菱形;
(2)若∠BOC=120°,AB=6,求FC的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:A、对角线是否相互平分,能判定平行四边形;
B、其中四边形中三个角都为直角,能判定矩形;
C、对角线相等的四边形不一定是矩形,不能判定形状;
D、两组对边是否分别相等,能判定平行四边形.
故选:B.
2.解:∵AB=2,BC=4,
∴矩形ABCD的面积为8,AC===2,
∴BO=CO=AC=,
∵对角线AC,BD交于点O,
∴△BOC的面积为2,
∵EO⊥AO,EF⊥DO,
∴S△BOC=S△BOE+S△COE,
2=CO×EO+BO×EF,
∴2=××EO+×EF,
∴(EO+EF)=4,
∴EO+EF=,
故选:A.
3.解:A、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC=∠BCD,
∴∠ABC=90°,
∴平行四边形ABCD为矩形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∴不能判定平行四边形ABCD为矩形,故选项B符合题意;
C、∵四边形ABCD是平行四边形,
∴AO=CO=AC,BO=DO=BD,
∵AO=BO,
∴AC=BD,
∴平行四边形ABCD为矩形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,
∴AO=CO=AC,BO=DO=BD,
∵AO=DO,
∴AC=BD,
∴平行四边形ABCD为矩形,故选项D不符合题意;
故选:B.
4.解:∵EF是BD的垂直平分线,
∴OB=OD,
∵∠OBF=∠ODE,∠BOF=∠DOE,
∴△BOF≌△DOE,则OE=OF,
∵∠OBF=∠ABD,
∵BD==10cm,
∴BO=5cm,
∴FO=5×cm=cm,
∴EF=2FO=cm.
故选:C.
5.解:如图,过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,延长CA交x轴于点H,
∵四边形AOBC是矩形,
∴AC∥OB,AC=OB,
∴∠CAF=∠BOE=∠CHO,
在△ACF和△OBE中,
,
∴△CAF≌△BOE(AAS),
∴BE=CF=4﹣1=3,
∵∠AOD+∠BOE=∠BOE+∠OBE=90°,
∴∠AOD=∠OBE,
∵∠ADO=∠OEB=90°,
∴OE=,即点B(,3),
∴AF=OE=,
∴点C的横坐标为:﹣(2﹣)=﹣,
∴点C(﹣,4).
故选:A.
6.解:∵四边形ABCD是矩形,
∴AD∥BC,∠BAD=∠ABC=∠ADC=90°,OA=OC,OD=OB,AC=BD,
∴OA=OD=OC=OB,
∵AE平分∠BAD,
∴∠DAE=45°,
∵∠CAE=15°,
∴∠DAC=45°﹣15°=30°,
∴∠ACD=90°﹣∠DAC=90°﹣30°=60°,
∵OD=OC,
∴△ODC是等边三角形,故①正确;
∵AD∥BC,
∴∠ACB=∠DAC=30°,
∵∠ABC=90°,
∴AC=2AB,
而AC>BC,
∴2AB>BC,故②错误;
∵OA=OC,
∴S△AOB=S△BOC、S△AOE=S△COE,故③、④正确;
故选:C.
7.解:如图,连接CE,
∵矩形ABCD中,AB=6,BC=8,
∴AD=BC=8,CD=AB=6,OA=OC,
∵OE⊥AC,
∴OE垂直平分AC,
∴AE=CE,
设AE=CE=x,则DE=8﹣x,
在Rt△CDE中,CD2+DE2=CE2,
即62+(8﹣x)2=x2,
解得x=,
即AE的长为.
故选:B.
8.解:∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵AE垂直平分OB,
∴AB=AO,
∴OA=AB=OB,
∵AE=2,
∴OE=2,
∴OD=OB=2OE=4;
故选:C.
二.填空题(共4小题,满分20分)
9.解:∵x>4,
∴点P在BC上时,
∵△APE的面积等于5cm2,
∴S长方形ABCD﹣S△CPE﹣S△ADE﹣S△ABP=5,
∴3×4﹣(3+4﹣x)×2﹣×2×3﹣×4×(x﹣4)=5,
∴x=5;
∴x=5秒时,△APE的面积等于5cm2.
故答案为:5.
10.解:延长EF和BC,交于点G
∵矩形ABCD中,∠B的角平分线BE与AD交于点E,
∴∠ABE=∠AEB=45°,
∴AB=AE=6,
∴直角三角形ABE中,BE==6,
又∵∠BED的角平分线EF与DC交于点F,
∴∠BEG=∠DEF,
∵AD∥BC,
∴∠G=∠DEF,
∴∠BEG=∠G,
∴BG=BE=6,
∵∠G=∠DEF,∠EFD=∠GFC,
设CG=x,DE=2x,则AD=6+2x=BC,
∵BG=BC+CG,
∴6=6+2x+x
解得x=2﹣2,
∴BC=6+2(2﹣2)=4+2,
故答案为:4+2.
11.解:∵四边形ABCD是矩形,
∴∠ABC=90°,
由勾股定理得:AC===5,
有三种情况:
①当AB=BP=3时,如图1,过B作BM⊥AC于M,
∵S△ABC=,
∴=,
解得:BM=,
∵AB=BP=3,BM⊥AC,
∴AM=PM==,
∴AP=AM+PM=,
∴△PAB的面积S==××=;
②当AB=AP=3时,如图2,
∵BM=,
∴△PAB的面积S=
=
=;
③作AB的垂直平分线NQ,交AB于N,交AC于P,如图3,则AP=BP,BN=AN==,
∵四边形ABCD是矩形,NQ⊥AB,
∴PN∥BC,
∵AN=BN,
∴AP=CP,
∴PN=BC==2,
∴△PAB的面积S=
=2
=3;
即△PAB的面积为或或3,
故答案为:或或3.
12.解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故答案为:10.
三.解答题(共8小题,满分60分)
13.(1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即 EF=BC.
∵在 ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形;14.(1)解:∵|a﹣4|+(b﹣6)2=0,
∵|a﹣4|≥0,(b﹣6)2≥0,
∴a﹣4=0,b﹣6=0,
∴a=4,b=6;
故答案为:4;6;
(2)当t=2时,△PCQ是等腰直角三角形,理由如下:
设运动时间为t秒(0≤t≤4),
∴OP=t,AQ=6﹣t,
当t=2时,OP=2,AQ=6﹣2=4,
∴AP=OA﹣OP=4﹣2=2,
∵四边形OABC是矩形,
∴∠COA=∠OAB=∠B=90°,
在Rt△COA中,PC=,
在Rt△APQ中,PQ=,
在Rt△CBQ中,CQ=,
∴CQ=PQ,PC2=PQ2+CQ2,
∴△CPQ是等腰直角三角形.
15.(1)证明:连接BD,交AC于点O,如图所示:
∵四边形ABCD是平行四边形,
∴BO=DO,
∵BE=EF,
∴OE是△BDF的中位线,
∴OE∥DF,
即DF∥AC;
(2)证明:如图所示:
由(1)得:DF∥AC,
∴∠DFG=∠CEG,∠GDF=∠GCE,
∵G是CD的中点,
∴DG=CG,
在△DFG和△CEG中,
,
∴△DFG≌△CEG(AAS),
∴FG=EG,
∴四边形CFDE是平行四边形,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵2AB=BF,
∴2CD=BF,
又∵EF=BE,
∴CD=EF,
∴平行四边形CFDE是矩形.
16.证明:∵PQ∥BC,
∴∠DEC=∠BCE,∠DFC=∠GCF,
∵CE平分∠BCA,CF平分∠ACG,
∴∠BCE=∠DCE,∠DCF=∠GCF,
∴∠DEC=∠DCE,∠DFC=∠DCF,
∴DE=DC,DF=DC,
∴DE=DF,
∵点D是边AC的中点,
∴AD=CD,
∴四边形AECF是平行四边形,
∵∠BCA+∠ACG=180°,
∴∠ECF=∠DCE+∠DCF=×180°=90°,
∴平行四边形AECF是矩形.
17.证明:(1)∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形;
(2)如图,连接OP,
∵AD=12,AB=5,
∴BD===13,
∴BO=OD=AO=CO=,
∵S△AOD=S矩形ABCD=×12×5=15,
∴S△AOP+S△POD=15,
∴××FP+××EP=15,
∴PE+PF=.
18.证明:∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,∠BAD=∠CAD.
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN.
∴∠DAE=90°,
∵CE⊥AN,
∴∠AEC=90°.
∴四边形ADCE为矩形.
19.(1)证明:∵CE∥BD,DE∥AC,
∴四边形ODEC是平行四边形.
又∵菱形ABCD,
∴AC⊥BD,∴∠DOC=90°.
∴四边形ODEC是矩形.
(2)解:
20.(1)证明:∵EF垂直平分BD,
∴EB=ED,FB=FD,BO=DO,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠OBF=∠ODE,
∵∠DOE=∠BOF,
∴△EOD≌△FOB(AAS),
∴DE=BF,
∴EB=ED=FB=FD,
∴四边形BEDF是菱形;
(2)解:∵四边形ABCD是矩形,
∴OB=OC,CD=AB=6,
∴∠OBC=∠OCB,
∵∠BOC=120°,
∴∠OBC=∠OCB=30°,
∵四边形EBFD为菱形,
∴FB=FD,
∴∠FBD=∠FDB=30°,
∴∠DFC=60°,
∴∠FDC=30°,
设CF=x,则FD=2x,
根据勾股定理得:(2x)2﹣x2=62,
解得:x=2,
∴FC的长为2.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
