2021-2022学年沪科版数学九年级下册24.4直线与圆的位置关系 课后提升(word版 含解析)
文档属性
| 名称 | 2021-2022学年沪科版数学九年级下册24.4直线与圆的位置关系 课后提升(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 10:02:40 | ||
图片预览



文档简介
直线与圆的位置关系
一、单选题
1.在同一平面内,有一半径为6的⊙O和直线m,直线m上有一点P,且OP=4;则直线m与⊙O的位置关系是 ( )
A.相交 B.相离 C.相切 D.不能确定
2.如图,在⊙O中,弦AB=10,PA=6㎝,OP=5㎝,则⊙O的半径R等于( )
A.7㎝ B.㎝ C.49㎝ D.㎝
3.如图,已知⊙C的半径为3,圆外一点O满足OC=5,点P为⊙C上一动点,经过点O的直线l上有两点A、B,且OA=OB,∠APB=90°,l不经过点C,则AB的最小值( )
A.2 B.4 C.5 D.6
4.如图,半径的⊙M在轴上平移,且圆心M在x轴上,当⊙M与直线相切时,圆心M的坐标为( )
A.(0,0) B.(2,0) C.(-6,0) D.(2,0) 或(-6,0)
5.如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,过点C作⊙O的切线,交AB的延长线于点D.设∠A=α,∠D=β,则( )
A.α﹣β=90° B.α+β=90° C.2α+β=90° D.α+2β=90°
6.如图,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一过点C的动圆O与斜边AB相切于动点P,连接CP.随着切点P的位置不同,则圆O的半径最小值为( )
A.2.5 B.2.4 C.2.2 D.1.2
7.如图,PA,PB是的切线,A,B是切点,点C是劣弧上的一个点,若,则的度数是( )
A. B. C. D.
8.如图,AB为⊙O的直径,直线AC与⊙O相切于点A,点E为半圆弧的中点,连接OC交⊙O于点D,连接ED.若∠CAD=20°,则∠EDO的度数为( )
A.20° B.25° C.30° D.35°
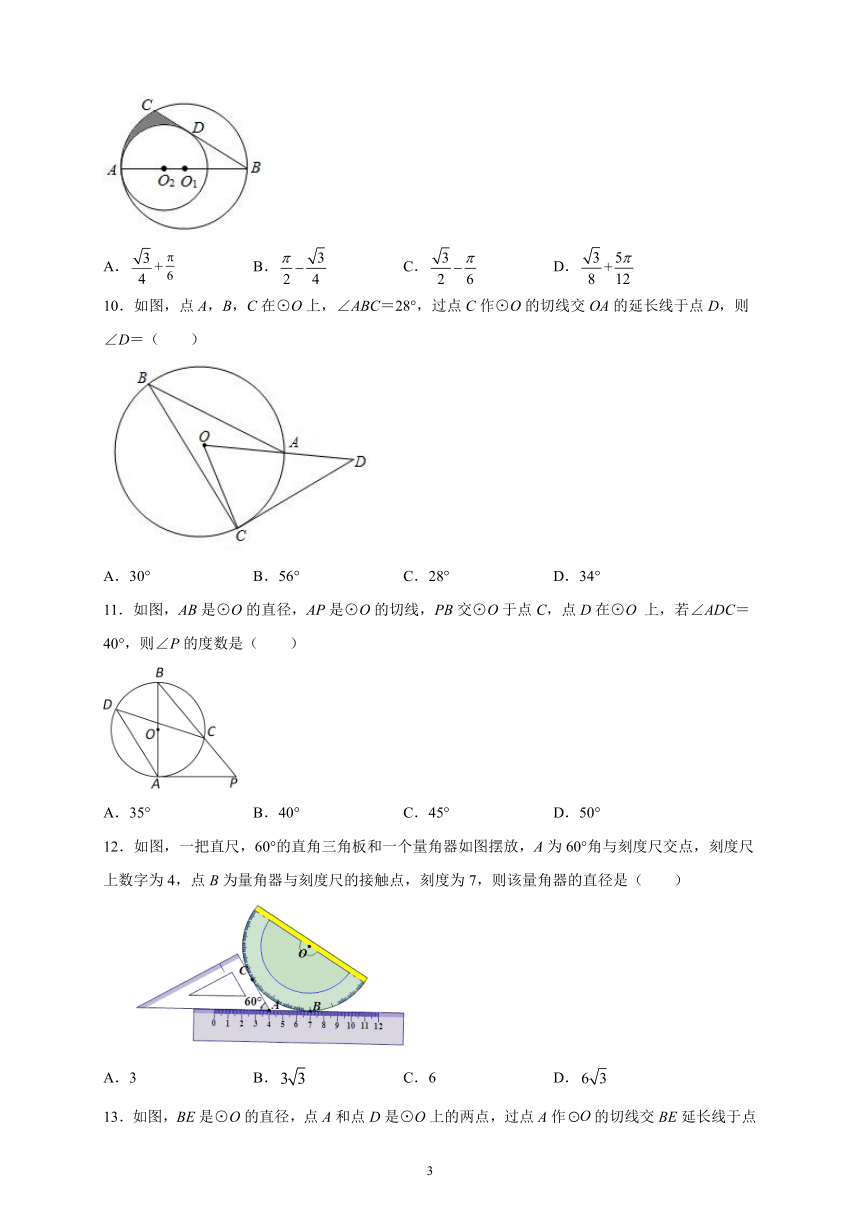
9.如图,AB是⊙O1的直径,点O2在AB上,⊙O2经过点A,⊙O1的弦BC与⊙O2相切于点D,若AB=6,O1O2=1,则由弧AC、弧AD与线段CD围成阴影部分的面积为( )
A.+ B. C. D.
10.如图,点A,B,C在⊙O上,∠ABC=28°,过点C作⊙O的切线交OA的延长线于点D,则∠D=( )
A.30° B.56° C.28° D.34°
11.如图,AB是⊙O的直径,AP是⊙O的切线,PB交⊙O于点C,点D在⊙O 上,若∠ADC=40°,则∠P的度数是( )
A.35° B.40° C.45° D.50°
12.如图,一把直尺,60°的直角三角板和一个量角器如图摆放,A为60°角与刻度尺交点,刻度尺上数字为4,点B为量角器与刻度尺的接触点,刻度为7,则该量角器的直径是( )
A.3 B. C.6 D.
13.如图,BE是⊙O的直径,点A和点D是⊙O上的两点,过点A作的切线交BE延长线于点C,若∠ADE=36°,则∠C的度数是( )
A.18° B.28° C.36° D.45°
14.如图,已知AB是的直径,C是AB延长线上一点,CE是的切线,切点为D,过点A作于点E,交于点F,连接OD、AD、BF.则下列结论不一定正确的是( )
A. B.AD平分 C. D.
15.如图,在中,以AB为直径的圆交AC于点D,的切线DE交BC于点E,若,于点E且,则的半径为( ).
A.4 B. C.2 D.
二、填空题
16.如图,PA,PB分别切于点A,B,,若点C在上,且不与A,B重合,则的度数是______.
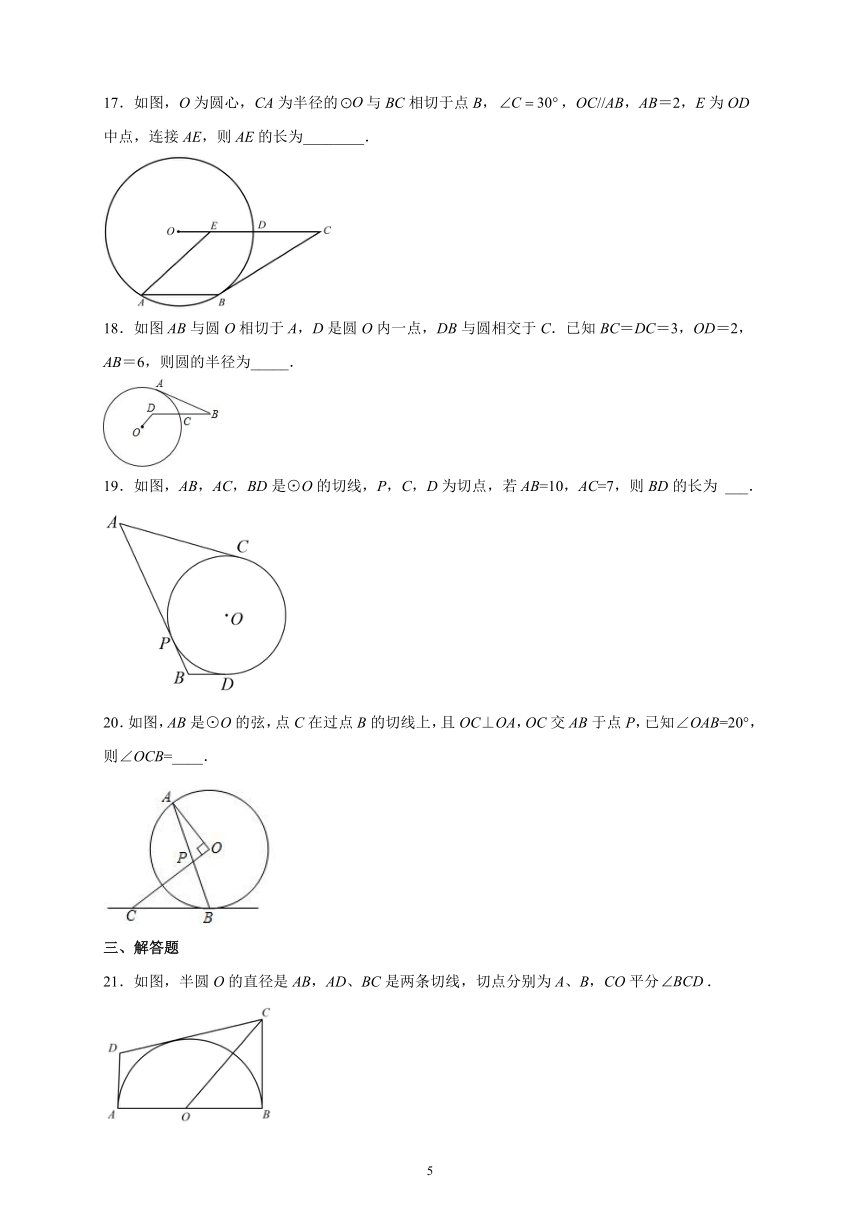
17.如图,O为圆心,CA为半径的与BC相切于点B,,OC//AB,AB=2,E为OD中点,连接AE,则AE的长为________.
18.如图AB与圆O相切于A,D是圆O内一点,DB与圆相交于C.已知BC=DC=3,OD=2,AB=6,则圆的半径为_____.
19.如图,AB,AC,BD是⊙O的切线,P,C,D为切点,若AB=10,AC=7,则BD的长为 ___.
20.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=20°,则∠OCB=____.
三、解答题
21.如图,半圆O的直径是AB,AD、BC是两条切线,切点分别为A、B,CO平分.
(1)求证:CD是半圈O的切线.
(2)若,,求BC和AB的长.
22.如图,AB是⊙O的弦,C为⊙O上一点,过点C作AB的垂线与AB的延长线交于点D,连接BO并延长,与⊙O交于点E,连接EC,.
(1)求证:CD是⊙O的切线;
(2)若,,求AB的长.
23.如图,在△ABC中,以AB为直径的⊙O与AC交于D点,过点D作DF⊥BC交AB的延长线于点E,垂足为F,∠FDB=∠A.
(1)判断DE与⊙O的位置关系并说明理由.
(2)若⊙O半径R=5,,求AC长.
24.如图1,AB是⊙O的直径,C,D为⊙O上两点,BD和过点C的切线互相垂直,垂足为E.
(1)求证:BC平分∠DBA;
(2)如图2,连接AC,当BD=3,AC=时,求⊙O的半径.
25.已知AB是⊙O的直径,弦CD与AB相交于点E,过点C作⊙O的切线,与BA的延长线交于点P,∠BPC=38°.
(1)如图①,连接OD,若D为的中点,求∠ODC的大小;
(2)如图②,连接BD,若DE=DB,求∠PBD的大小.
试卷第1页,共3页
参考答案:
1.A
解:∵⊙O的半径为6,直线m上有一动点P,OP=4,
∴直线与⊙O相交.
故选:A.
2.A
解:将OP向两方延长,
设OC=xcm,则CP=(x+5)cm,PD=(x-5)cm
根据相交弦定理,AP BP=CP DP,即
6×4=(x+5)(x-5)
解得 =49,x=7或x=-7(负值舍去),
则⊙O的半径等于7cm
故选A
3.B
解:连接OP,PC,OC,
∵OP≥OC-PC=2,
∴当点O,P,C三点共线时,OP最小,最小值为2,
∵OA=OB,∠APB=90°,
∴AB=2OP,
当O,P,C三点共线时,AB有最小值为2OP=4,
故选:B.
4.D
解:①当圆位于直线右侧并与直线相切时,连接MA,如下图所示:
∵
∴,,是等腰直角三角形,
∴
∵
∴是等腰直角三角形,
∴⊙M与直线AB相切于点A
∵
∴
∴圆心M的坐标为;
②当圆位于直线左侧并与直线相切时,过点M作于点C,如下图所示:
∵⊙M与直线AB相切,
∴
根据直线AB的解析式:可知
∴是等腰直角三角形
∴
∵
∴圆心M的坐标为,
综上所述:圆心M的坐标为或,
故选:D.
5.C
解:连接OC,如图,
∵⊙O是Rt△ABC的外接圆,∠ACB=90°,
∴AB是直径,
∵∠A=α,
∴∠BOC=2∠A=2α,
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,
∴∠D=90°﹣∠BOC=90°﹣2α=β,
∴2α+β=90°.
故选:C.
6.D
解:如图所示,连接OC,OP,设圆O的半径为r
∴OC=OP,
∵,
∴,
∴当P、O、C三点共线且CP⊥AB时,r有最小值,
∵AC=3,BC=4,∠ACB=90°,
∴,
∵,
∴,
∴r的最小值为1.2,
故选D.
7.B
解:连接OA,OB,
∵ PA,PB是的切线,
∴,
∵,
∴优弧AB所对的圆心角是,
∴,
∴,
故选:B.
8.B
解:连接OE,如图,
∵直线AC与⊙O相切于点A,
∴AB⊥AC,
∴∠BAC=90°,
∵∠BAD=90°﹣∠CAD=90°﹣20°=70°,
∵OA=OD,
∴∠ODA=∠OAD=70°,
∵点E为半圆弧的中点,
∴OE⊥AB,
∴∠AOE=90°,
∴∠ADE∠AOE=45°,
∴∠EDO=∠ODA﹣∠ADE=70°﹣45°=25°.
故选:B.
9.A
解:连接,,,过作于,则,
,
,
,
,
,
,
切于,
,
即,
,
,
在△中,,,
,
由勾股定理得:,,
,过,
,
,,
,
,
阴影部分的面积
,
故选:A.
10.D
解:∵CD与⊙O相切,
∴OC⊥CD,
∴∠OCD=90°,
由圆周角定理可知:∠COD=2∠CBA=56°,
∴∠D=90°-∠OCD=90°-56°=34°,
故选:D.
11.D
解:,
,
为的切线,点为切点,
,
,
故选:D.
12.D
解:如图所示,连接OA,OB,OC,
∵三角板的顶角为60°,
∴∠CAB=120°,
∵AC,AB,与扇形分别交于一点,
∴AC,AB是扇形O所在圆的切线,
∴OC⊥AC,OB⊥AB,
在Rt△AOC与Rt△AOB中,
∴Rt△AOC≌Rt△AOB,
∴∠OAC=∠OAB=60°,
由题可知AB=7-4=3,
∴OB=AB tan60°= ,
∴直径为,
故选:D.
13.A
解:连接OA,DE,如图,
∵AC是的切线,OA是的半径,
∴OAAC
∠OAC=90°
∠ADE=36°
AOE=2∠ADE=72°
∠C=90°-∠AOE=90°-72°=18°
故选:A.
14.D
解:∵AB是的直径,
∴
∵CE是的切线,切点为D,
∴
,故A选项正确,
,
即AD平分,故B选项正确,
设交于点,如图,
∵,
∴四边形是矩形
,
,故C选项正确
若,则
由于点不一定是的中点,故D选项不正确;
故选D
15.C
解:连接OD、BD,
∵∠CAB=30°,OD=OA,
∴∠CAB=∠ODA=30°,
∴∠BOD=∠CAB+∠ODA=60°,
∵OD=OB,
∴△BOD是等边三角形,
∵DE是⊙O的切线,
∴∠ODE=90°,
∴∠BDE=30°,
∵DE⊥BC于点E且BE=1,
∴BD=2BE=2,
∴OB=BD=2,
即⊙O的半径为2,
故选:C.
.
16.55°或125°
解:连接
PA,PB分别切于点A,B,,
当在优弧上时,
点在劣弧上时,四边形是圆内接四边形
则
故答案为:55°或125°
17.
解:如图所示,连接OA,OB,BE,BD,过点O作OH⊥AB于H,
∵BC是圆O的切线,
∴∠OBC=90°,
又∵∠C=30°,
∴∠BOC=60°,
∵OC∥AB,
∴∠OBA=∠BOC=60°,
∵OA=OB,OB=OD,
∴△ABO是等边三角形,△OBD是等边三角形,
∴,OA=AB=2,
∴,
∵E是OD的中点,
∴BE⊥OD,
又∵OH⊥AB,OC∥AB,
∴四边形OHBE是矩形,
∴,∠ABE=90°,
∴,
故答案为:.
18.
解:连接BC并延长,交圆于F,过O作OE⊥BF,连接
∵BA是圆O的切线,切点为A,
在中,
则
又
AB2=BC BF,
∵BC=DC=3,AB=6,
∴BF=12,CF=9,
∴DE=,OD=2,
∴OE===,CE=,
∴OC===.
故答案为:.
19.
解:∵AC与⊙O相切于点C、AB与⊙O相切于点P,
∴AC=AP=7,
∵AB=10,
∴BP=AB-AP=10-7=3,
∵BD与⊙O相切于点D、BP与⊙O相切于点P,
∴BD=BP=3,
∴BD的长为3,
故答案为:3.
20.40°##40度
解:连接OB,
∵OB是的切线,
∴,
∴,
∵,
∴,
∵,,
∴,
∴,
∴,
∴,
故答案为:40°.
21.(1)见解析 (2)
(1)
证明:如图,过点O作于点E.
∵BC是半圆O的切线,
∴.
∵CO平分,
∴,
∴CD是半圆O的切线.
(2)
解:∵AD,CD,BC是半圆O的切线,
∴,.
∵,
∴,
∴.
如图,过点D作于点F,故四边形DABF为矩形,
∴,,
∴.
在中,由勾股定理得,
∴.
22.(1)见解析; (2).
(1)
证明:连接OC,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴CD是⊙O的切线;
(2)
解:连接AC,BC,
∵BE是⊙O的直径,
∴,
∴,
∵,
∴,
∵,
∴,即:,
∵,
∴,
∵,
∴,
∴,
∴.
23.(1)DE与⊙O相切,理由见解析; (2)
(1)
解:DE与⊙O 相切;
理由如下:
如图:连接OD,
,
,
,
,
是⊙O的直径,
,
,
,
与⊙O相切;
(2)
解⊙O的半径,
,
,设DB=3x,则AD=4x,AB=5x,
∴5x=10,x=2,
∴AD=8,DB=6,
,
,
,
又,
,
,即,
.
24.(1)见解析 (2)
(1)
解:证明:如图1,连接,
与相切于点,
,
,
,
,
,
,
,
平分.
(2)
如图2,连接交于点,
,
,
,,
,
,,,
,
设的半径为,则,
,
,,
,
,
解得,(不符合题意,舍去),
的半径为.
25.(1) (2)
(1)
如图1,连接,
图1
∵D为的中点,
∴,
∴,
∵是的切线,为切点,
∴,
∴,
∴,
∵,
∴,
∴
∴;
(2)
如图2,连接,
图2
∵是的切线,为切点,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
答案第1页,共2页
一、单选题
1.在同一平面内,有一半径为6的⊙O和直线m,直线m上有一点P,且OP=4;则直线m与⊙O的位置关系是 ( )
A.相交 B.相离 C.相切 D.不能确定
2.如图,在⊙O中,弦AB=10,PA=6㎝,OP=5㎝,则⊙O的半径R等于( )
A.7㎝ B.㎝ C.49㎝ D.㎝
3.如图,已知⊙C的半径为3,圆外一点O满足OC=5,点P为⊙C上一动点,经过点O的直线l上有两点A、B,且OA=OB,∠APB=90°,l不经过点C,则AB的最小值( )
A.2 B.4 C.5 D.6
4.如图,半径的⊙M在轴上平移,且圆心M在x轴上,当⊙M与直线相切时,圆心M的坐标为( )
A.(0,0) B.(2,0) C.(-6,0) D.(2,0) 或(-6,0)
5.如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,过点C作⊙O的切线,交AB的延长线于点D.设∠A=α,∠D=β,则( )
A.α﹣β=90° B.α+β=90° C.2α+β=90° D.α+2β=90°
6.如图,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一过点C的动圆O与斜边AB相切于动点P,连接CP.随着切点P的位置不同,则圆O的半径最小值为( )
A.2.5 B.2.4 C.2.2 D.1.2
7.如图,PA,PB是的切线,A,B是切点,点C是劣弧上的一个点,若,则的度数是( )
A. B. C. D.
8.如图,AB为⊙O的直径,直线AC与⊙O相切于点A,点E为半圆弧的中点,连接OC交⊙O于点D,连接ED.若∠CAD=20°,则∠EDO的度数为( )
A.20° B.25° C.30° D.35°
9.如图,AB是⊙O1的直径,点O2在AB上,⊙O2经过点A,⊙O1的弦BC与⊙O2相切于点D,若AB=6,O1O2=1,则由弧AC、弧AD与线段CD围成阴影部分的面积为( )
A.+ B. C. D.
10.如图,点A,B,C在⊙O上,∠ABC=28°,过点C作⊙O的切线交OA的延长线于点D,则∠D=( )
A.30° B.56° C.28° D.34°
11.如图,AB是⊙O的直径,AP是⊙O的切线,PB交⊙O于点C,点D在⊙O 上,若∠ADC=40°,则∠P的度数是( )
A.35° B.40° C.45° D.50°
12.如图,一把直尺,60°的直角三角板和一个量角器如图摆放,A为60°角与刻度尺交点,刻度尺上数字为4,点B为量角器与刻度尺的接触点,刻度为7,则该量角器的直径是( )
A.3 B. C.6 D.
13.如图,BE是⊙O的直径,点A和点D是⊙O上的两点,过点A作的切线交BE延长线于点C,若∠ADE=36°,则∠C的度数是( )
A.18° B.28° C.36° D.45°
14.如图,已知AB是的直径,C是AB延长线上一点,CE是的切线,切点为D,过点A作于点E,交于点F,连接OD、AD、BF.则下列结论不一定正确的是( )
A. B.AD平分 C. D.
15.如图,在中,以AB为直径的圆交AC于点D,的切线DE交BC于点E,若,于点E且,则的半径为( ).
A.4 B. C.2 D.
二、填空题
16.如图,PA,PB分别切于点A,B,,若点C在上,且不与A,B重合,则的度数是______.
17.如图,O为圆心,CA为半径的与BC相切于点B,,OC//AB,AB=2,E为OD中点,连接AE,则AE的长为________.
18.如图AB与圆O相切于A,D是圆O内一点,DB与圆相交于C.已知BC=DC=3,OD=2,AB=6,则圆的半径为_____.
19.如图,AB,AC,BD是⊙O的切线,P,C,D为切点,若AB=10,AC=7,则BD的长为 ___.
20.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=20°,则∠OCB=____.
三、解答题
21.如图,半圆O的直径是AB,AD、BC是两条切线,切点分别为A、B,CO平分.
(1)求证:CD是半圈O的切线.
(2)若,,求BC和AB的长.
22.如图,AB是⊙O的弦,C为⊙O上一点,过点C作AB的垂线与AB的延长线交于点D,连接BO并延长,与⊙O交于点E,连接EC,.
(1)求证:CD是⊙O的切线;
(2)若,,求AB的长.
23.如图,在△ABC中,以AB为直径的⊙O与AC交于D点,过点D作DF⊥BC交AB的延长线于点E,垂足为F,∠FDB=∠A.
(1)判断DE与⊙O的位置关系并说明理由.
(2)若⊙O半径R=5,,求AC长.
24.如图1,AB是⊙O的直径,C,D为⊙O上两点,BD和过点C的切线互相垂直,垂足为E.
(1)求证:BC平分∠DBA;
(2)如图2,连接AC,当BD=3,AC=时,求⊙O的半径.
25.已知AB是⊙O的直径,弦CD与AB相交于点E,过点C作⊙O的切线,与BA的延长线交于点P,∠BPC=38°.
(1)如图①,连接OD,若D为的中点,求∠ODC的大小;
(2)如图②,连接BD,若DE=DB,求∠PBD的大小.
试卷第1页,共3页
参考答案:
1.A
解:∵⊙O的半径为6,直线m上有一动点P,OP=4,
∴直线与⊙O相交.
故选:A.
2.A
解:将OP向两方延长,
设OC=xcm,则CP=(x+5)cm,PD=(x-5)cm
根据相交弦定理,AP BP=CP DP,即
6×4=(x+5)(x-5)
解得 =49,x=7或x=-7(负值舍去),
则⊙O的半径等于7cm
故选A
3.B
解:连接OP,PC,OC,
∵OP≥OC-PC=2,
∴当点O,P,C三点共线时,OP最小,最小值为2,
∵OA=OB,∠APB=90°,
∴AB=2OP,
当O,P,C三点共线时,AB有最小值为2OP=4,
故选:B.
4.D
解:①当圆位于直线右侧并与直线相切时,连接MA,如下图所示:
∵
∴,,是等腰直角三角形,
∴
∵
∴是等腰直角三角形,
∴⊙M与直线AB相切于点A
∵
∴
∴圆心M的坐标为;
②当圆位于直线左侧并与直线相切时,过点M作于点C,如下图所示:
∵⊙M与直线AB相切,
∴
根据直线AB的解析式:可知
∴是等腰直角三角形
∴
∵
∴圆心M的坐标为,
综上所述:圆心M的坐标为或,
故选:D.
5.C
解:连接OC,如图,
∵⊙O是Rt△ABC的外接圆,∠ACB=90°,
∴AB是直径,
∵∠A=α,
∴∠BOC=2∠A=2α,
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,
∴∠D=90°﹣∠BOC=90°﹣2α=β,
∴2α+β=90°.
故选:C.
6.D
解:如图所示,连接OC,OP,设圆O的半径为r
∴OC=OP,
∵,
∴,
∴当P、O、C三点共线且CP⊥AB时,r有最小值,
∵AC=3,BC=4,∠ACB=90°,
∴,
∵,
∴,
∴r的最小值为1.2,
故选D.
7.B
解:连接OA,OB,
∵ PA,PB是的切线,
∴,
∵,
∴优弧AB所对的圆心角是,
∴,
∴,
故选:B.
8.B
解:连接OE,如图,
∵直线AC与⊙O相切于点A,
∴AB⊥AC,
∴∠BAC=90°,
∵∠BAD=90°﹣∠CAD=90°﹣20°=70°,
∵OA=OD,
∴∠ODA=∠OAD=70°,
∵点E为半圆弧的中点,
∴OE⊥AB,
∴∠AOE=90°,
∴∠ADE∠AOE=45°,
∴∠EDO=∠ODA﹣∠ADE=70°﹣45°=25°.
故选:B.
9.A
解:连接,,,过作于,则,
,
,
,
,
,
,
切于,
,
即,
,
,
在△中,,,
,
由勾股定理得:,,
,过,
,
,,
,
,
阴影部分的面积
,
故选:A.
10.D
解:∵CD与⊙O相切,
∴OC⊥CD,
∴∠OCD=90°,
由圆周角定理可知:∠COD=2∠CBA=56°,
∴∠D=90°-∠OCD=90°-56°=34°,
故选:D.
11.D
解:,
,
为的切线,点为切点,
,
,
故选:D.
12.D
解:如图所示,连接OA,OB,OC,
∵三角板的顶角为60°,
∴∠CAB=120°,
∵AC,AB,与扇形分别交于一点,
∴AC,AB是扇形O所在圆的切线,
∴OC⊥AC,OB⊥AB,
在Rt△AOC与Rt△AOB中,
∴Rt△AOC≌Rt△AOB,
∴∠OAC=∠OAB=60°,
由题可知AB=7-4=3,
∴OB=AB tan60°= ,
∴直径为,
故选:D.
13.A
解:连接OA,DE,如图,
∵AC是的切线,OA是的半径,
∴OAAC
∠OAC=90°
∠ADE=36°
AOE=2∠ADE=72°
∠C=90°-∠AOE=90°-72°=18°
故选:A.
14.D
解:∵AB是的直径,
∴
∵CE是的切线,切点为D,
∴
,故A选项正确,
,
即AD平分,故B选项正确,
设交于点,如图,
∵,
∴四边形是矩形
,
,故C选项正确
若,则
由于点不一定是的中点,故D选项不正确;
故选D
15.C
解:连接OD、BD,
∵∠CAB=30°,OD=OA,
∴∠CAB=∠ODA=30°,
∴∠BOD=∠CAB+∠ODA=60°,
∵OD=OB,
∴△BOD是等边三角形,
∵DE是⊙O的切线,
∴∠ODE=90°,
∴∠BDE=30°,
∵DE⊥BC于点E且BE=1,
∴BD=2BE=2,
∴OB=BD=2,
即⊙O的半径为2,
故选:C.
.
16.55°或125°
解:连接
PA,PB分别切于点A,B,,
当在优弧上时,
点在劣弧上时,四边形是圆内接四边形
则
故答案为:55°或125°
17.
解:如图所示,连接OA,OB,BE,BD,过点O作OH⊥AB于H,
∵BC是圆O的切线,
∴∠OBC=90°,
又∵∠C=30°,
∴∠BOC=60°,
∵OC∥AB,
∴∠OBA=∠BOC=60°,
∵OA=OB,OB=OD,
∴△ABO是等边三角形,△OBD是等边三角形,
∴,OA=AB=2,
∴,
∵E是OD的中点,
∴BE⊥OD,
又∵OH⊥AB,OC∥AB,
∴四边形OHBE是矩形,
∴,∠ABE=90°,
∴,
故答案为:.
18.
解:连接BC并延长,交圆于F,过O作OE⊥BF,连接
∵BA是圆O的切线,切点为A,
在中,
则
又
AB2=BC BF,
∵BC=DC=3,AB=6,
∴BF=12,CF=9,
∴DE=,OD=2,
∴OE===,CE=,
∴OC===.
故答案为:.
19.
解:∵AC与⊙O相切于点C、AB与⊙O相切于点P,
∴AC=AP=7,
∵AB=10,
∴BP=AB-AP=10-7=3,
∵BD与⊙O相切于点D、BP与⊙O相切于点P,
∴BD=BP=3,
∴BD的长为3,
故答案为:3.
20.40°##40度
解:连接OB,
∵OB是的切线,
∴,
∴,
∵,
∴,
∵,,
∴,
∴,
∴,
∴,
故答案为:40°.
21.(1)见解析 (2)
(1)
证明:如图,过点O作于点E.
∵BC是半圆O的切线,
∴.
∵CO平分,
∴,
∴CD是半圆O的切线.
(2)
解:∵AD,CD,BC是半圆O的切线,
∴,.
∵,
∴,
∴.
如图,过点D作于点F,故四边形DABF为矩形,
∴,,
∴.
在中,由勾股定理得,
∴.
22.(1)见解析; (2).
(1)
证明:连接OC,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴CD是⊙O的切线;
(2)
解:连接AC,BC,
∵BE是⊙O的直径,
∴,
∴,
∵,
∴,
∵,
∴,即:,
∵,
∴,
∵,
∴,
∴,
∴.
23.(1)DE与⊙O相切,理由见解析; (2)
(1)
解:DE与⊙O 相切;
理由如下:
如图:连接OD,
,
,
,
,
是⊙O的直径,
,
,
,
与⊙O相切;
(2)
解⊙O的半径,
,
,设DB=3x,则AD=4x,AB=5x,
∴5x=10,x=2,
∴AD=8,DB=6,
,
,
,
又,
,
,即,
.
24.(1)见解析 (2)
(1)
解:证明:如图1,连接,
与相切于点,
,
,
,
,
,
,
,
平分.
(2)
如图2,连接交于点,
,
,
,,
,
,,,
,
设的半径为,则,
,
,,
,
,
解得,(不符合题意,舍去),
的半径为.
25.(1) (2)
(1)
如图1,连接,
图1
∵D为的中点,
∴,
∴,
∵是的切线,为切点,
∴,
∴,
∴,
∵,
∴,
∴
∴;
(2)
如图2,连接,
图2
∵是的切线,为切点,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
答案第1页,共2页
