2021—2022学年苏科版数学八年级下册9.3平行四边形 基础解答题专题训练(word版 含答案)
文档属性
| 名称 | 2021—2022学年苏科版数学八年级下册9.3平行四边形 基础解答题专题训练(word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 418.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 10:04:33 | ||
图片预览




文档简介
2021-2022学年苏科版八年级数学下册《9-3平行四边形》基础解答题专题训练(附答案)
1.如图,已知 ABCD,E为BC边上的垂直平分线,BC=FC=2AB,且∠ABD=90°.
(1)求证:△ABD≌△CEF;
(2)连接AF,请判断四边形ABDF的形状,并说明理由.
2.如图,在△NMB中,BM=8,点A,C,D分别在边MB,BN,MN上,DA∥NB,DC∥MB,∠NDC=∠MDA.求四边形ABCD的周长.
3.如图,在平行四边形ABCD中,点E、F分别在边BC和AD上,且BE=DF.
求证:AE∥CF.
4.如图,四边形ABCD中,AB∥CD,AB=CD.AD与CB有什么关系?证明你的结论.
5.已知:如图,在 ABCD中,E,F分别为BC和AD上的点,BD和EF相交于点O,且OE=OF.求证:四边形AECF为平行四边形.
6.如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,求BD的长.
7.如图,AB,CD相交于点E且互相平分,F是BD延长线上一点,若∠FAC=2∠BAC,求证:AC+DF=AF.
8.如图,四边形ABCD是平行四边形,E,F是对角线AC的三等分点,连接BE,DF.证明:BE=DF.
9.如图,在平行四边形ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:△BOE≌△COD;
(2)若BC平分∠DBE,请判断并证明四边形BECD的形状.
10.已知:如图,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:(1)△AFD≌△CEB;
(2)四边形AECF是平行四边形.
11.如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,且AD=AF.
(1)判断四边形ABFC的形状并证明;
(2)若AB=3,∠ABC=60°,求EF的长.
12.如图,在平行四边形ABCD中,点F是AD中点,连接CF并延长交BA的延长线于点E.
(1)求证:AB=AE.
(2)若BC=2AE,∠E=31°,求∠DAB的度数.
13.已知: ABCD中,E、F是对角线BD上两点,连接AE、CF,若∠BAE=∠DCF.求证:AE=CF.
14.如图,E、F是 ABCD对角线AC上的两点,AF=CE.求证:BE=DF.
15.如图,将 ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF.求证:四边形AECF是平行四边形.
16.如图,平行四边形ABCD的对角线交于点E,若BC=4,BD=10,AC=6.
(1)求证:∠ACB=90°;
(2)求CD的长.
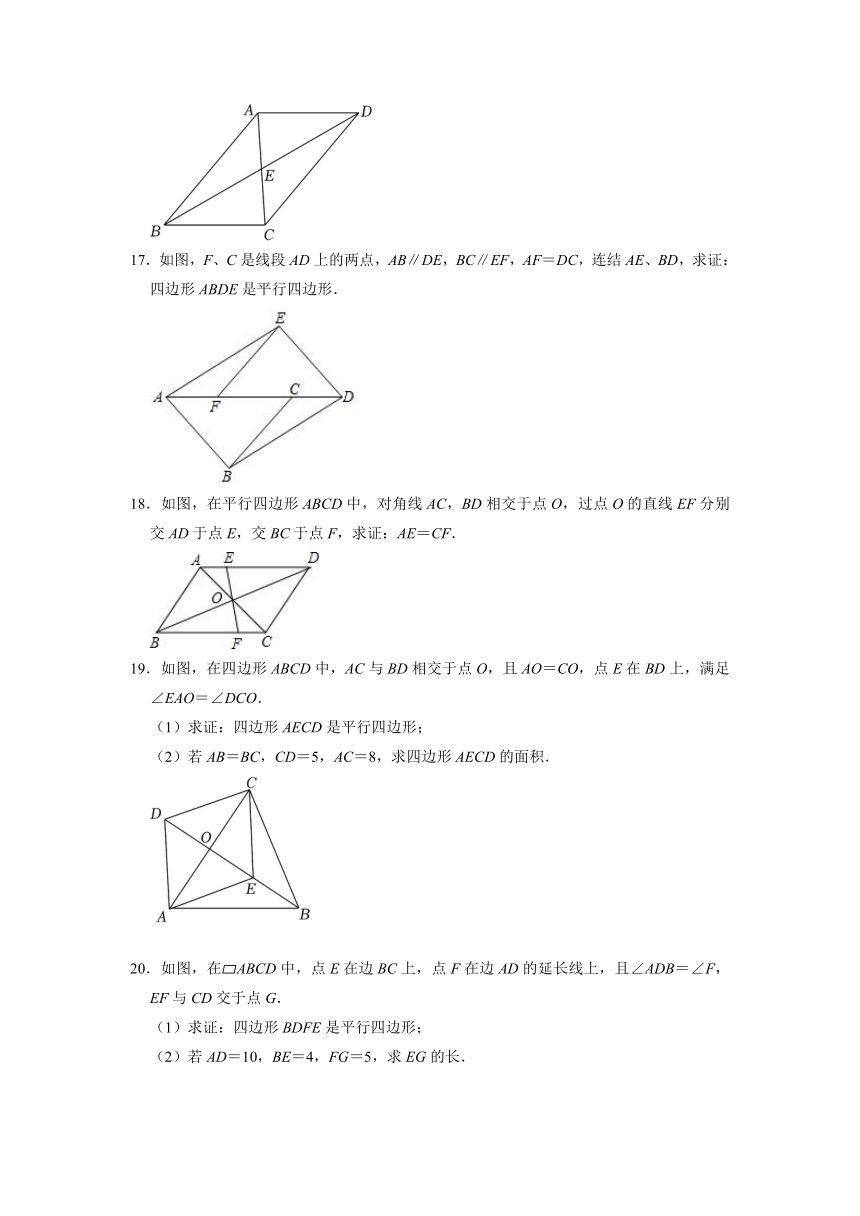
17.如图,F、C是线段AD上的两点,AB∥DE,BC∥EF,AF=DC,连结AE、BD,求证:四边形ABDE是平行四边形.
18.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O的直线EF分别交AD于点E,交BC于点F,求证:AE=CF.
19.如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=5,AC=8,求四边形AECD的面积.
20.如图,在 ABCD中,点E在边BC上,点F在边AD的延长线上,且∠ADB=∠F,EF与CD交于点G.
(1)求证:四边形BDFE是平行四边形;
(2)若AD=10,BE=4,FG=5,求EG的长.
21.已知:如图,点E,F在BD上,且AE=CF,BF=DE,∠AEB=∠CFD.求证:AC与BD互相平分.
22.如图,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,AB∥CD.求证:AC与BD互相平分.
23.如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC.
(1)求证:△ABE≌△FCE;
(2)若AD=AF,判断四边形ABFC是什么特殊四边形,并说明理由.
24.如图,在平行四边形ABCD中,DE,BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.求证:BD、EF互相平分.
25.如图,在 ABCD中,AE平分∠BAD交BD于点E,交BC于点M,CF平分∠BCD交BD于点F.
(1)求证:AE=CF;
(2)若∠ABC=70°,求∠AMB的度数.
26.如图,BD是 ABCD的对角线,∠BAD的平分线交BD于点E,∠BCD的平分线交BD于点F.求证:AE∥CF.
27.如图,点B,E,C,F在一条直线上,AB=DE,AB∥DE,BE=CF.
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形ACFD是平行四边形.
28.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在CA和AC的延长线上,且AE=CF,连接DE,BF.求证:DE=BF.
29.如图,在 ABCD中,E是CD边上的中点,AD,BE的延长线相交于点F.
(1)求证:△BCE≌△FDE.
(2)若DF=3,DE=2,求 ABCD的周长.
30.如图, ABCD对角线AC,BD相交于点O,E,F分别是OA,OC的中点,连接BE、DF.求证:BE=DF.
参考答案
1.(1)证明:∵四边形ABCD是平行四边形,
∴BC=AD,AB=CD,
∵E为BC边上的垂直平分线,
∴BC=2EC=2BE,∠FEC=90°,
∵BC=FC=2AB,
∴EC=AB=CD,BC=BF=FC,
∴△BCF是等边三角形,
∴AD=FC,
∴∠ABD=∠FEC=90°,
在Rt△ABD和Rt△CEF中,
,
∴Rt△ABD≌Rt△CEF(HL);
(2)解:四边形ABDF是矩形,理由如下:
∵△BCF是等边三角形,
∴BC=FC=2AB=2CD,
∴FD=CD=AB,
∵AB∥CD,
∴四边形ABDF是平行四边形,
∵∠ABD=90°,
∴四边形ABDF是矩形.
2.解:∵DA∥NB,DC∥MB,
∴∠NDC=∠M,四边形ABCD为平行四边形,
∴DC=AB,AD=BC,
∵∠NDC=∠MDA.
∴AD=AM,
∴四边形ABCD的周长=AB+BC+CD+AD=2AM+2AB=2BM=2×8=16.
3.证明:四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵BE=DF,
∴AD﹣DF=BC﹣BE,
即AF=CE,
∵AF∥CE,
∴四边形AECF是平行四边形,
∴AE∥CF.
4.解:AD=BC且AD∥BC.
证明:∵AB∥CD,
∴∠ABD=∠CDB.
在△ABD与△CDB中,
,
∴△ABD≌△CDB(SAS).
∴AD=BC,∠ADB=∠CBD.
∴AD∥BC.
5.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ODF=∠OBE,
在△DOF和△BOE中,
,
∴△DOF≌△BOE(AAS),
∴DF=BE,
∴AD﹣DF=BC﹣BE,
即AF=EC,
∴四边形AECF为平行四边形.
6.解:∵ ABCD的对角线AC与BD相交于点O,
∴BO=DO,OA=OC,BC=AD=5,
∵AB⊥AC,AB=3,
∴AC==4,
∴OA=2,
∴BO==,
∴BD=2BO=2.
故BD的长为2.
7.证明:连接AD、BC,
∵AB,CD相交于点E且互相平分,
∴四边形ACBD是平行四边形,
∴AC=BC,AC∥BC,
∴∠BAC=∠ABF,
∵∠FAC=2∠BAC,
∴∠FAB=∠BAC,
∴∠ABF=∠FAB,
∴AF=BF,
∵AC+DF=BD+DF=BF,
∴AC+DF=AF.
8.证明:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∴∠BAC=∠DCA,
∵E,F是对角线AC的三等分点,
∴AE=CF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
9.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,
,
∴△BOE≌△COD(AAS);
(2)解:四边形BECD是菱形;
证明:∵△BOE≌△COD,
∴OE=OD,BO=CO,
∴四边形BECD是平行四边形,
∵AE∥CD,
∴∠BCD=∠CBE,
∵BC平分∠DBE,
∴∠DBC=∠CBE,
∴∠DBC=∠DCB,
∴BD=DC,
∴四边形BECD是菱形.
10.证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D,
又∵E,F分别是AB,CD的中点,
∴AE=BE=AB,CF=DF=CD,
∴BE=DF,AE=CF,
在△AFD和△CEB中,
,
∴△AFD≌△CEB(SAS);
(2)由(1)知AE=CF,△AFD≌△CEB,
∴AF=CE,
∴四边形AECF是平行四边形.
11.解:(1)四边形ABFC是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
∵E为BC的中点,
∴EB=EC,
在△ABE和△FCE中,
,
∴△ABE≌△FCE(AAS),
∴AB=CF.
∵AB∥CF,
∴四边形ABFC是平行四边形,
∵AD=BC,AD=AF,
∴BC=AF,
∴四边形ABFC是矩形.
(2)∵四边形ABFC是矩形,
∴BC=AF,AF=EF,BE=CE,
∴AE=BE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴AB=AE=3,
∴EF=3.
12.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,BC=AD,
∴∠E=∠DCF,
∵点F是AD中点,
∴AF=DF,
∵∠EFA=∠CFD,
∴△AFE≌△DFC(AAS),
∴CD=AE,
∴AB=AE;
(2)解:由(1)可得AF=DF,BC=AD,
∵BC=2AE,
∴AE=AF,
∵∠E=31°,
∴∠AFE=∠E=31°,
∴∠DAB=2∠E=62°.
13.证明∵四边形ABCD为平行四边形
∴AB∥CD,AB=CD
∴∠ABD=∠CDB
∵∠BAE=∠DCF,CD=AB,∠ABD=∠BDC
∴△ABE≌△CDF
∴AE=CF
14.证明:∵AF=CE.
∴AE=CF,
∵在 ABCD中,AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
15.证明:连接AC,设AC与BD交于点O.如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵BE=DF,
∴OE=OF.
∴四边形AECF是平行四边形.
16.(1)证明:∵四边形ABCD是平行四边形,BD=10,AC=6,
∴BE=5,CE=3,
∵32+42=52,
即BE2=CE2+BC2,
∴△BEC是直角三角形,
即∠ACB=90°;
(2)解:∵四边形ABCD是平行四边形,∠ACB=90°,
∴AD∥BC,AD=BC=4,
∴∠CAD=90°,
在Rt△ACD中,由勾股定理得,CD=.
17.证明:∵AF=DC,
∴AF+FC=DC+FC,
∴AC=DF,
∵AB∥DE,
∴∠BAC=∠EDF,
∵BC∥EF,
∴∠ACB=∠EFD,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AB=DE,
又∵AB∥DE,
∴四边形ABDE是平行四边形.
18.证明:∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
∵,
∴△AOE≌△COF(ASA)
∴AE=CF.
19.(1)证明:在△AOE和△COD中,
,
∴△AOE≌△COD(ASA),
∴OD=OE,
又∵AO=CO,
∴四边形AECD是平行四边形;
(2)解:∵AB=BC,AO=CO,
∴OB⊥AC,
∴平行四边形AECD是菱形,
∵AC=8,
∴CO=AC=4,
在Rt△COD中,由勾股定理得:OD===3,
∴DE=2OD=6,
∴菱形AECD的面积=AC×DE=×8×6=24.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠ADB=∠F,
∴BD∥EF,
∴四边形BDFE是平行四边形;
(2)解:由(1)得:四边形BDFE是平行四边形,
∴DF=BE=4,
∵四边形ABCD是平行四边形,
∴BC=AD=10,
∴CE=BC﹣BE=10﹣4=6,AD∥BC,
∴△CEG∽△DFG,
∴=,
即=,
解得:EG=,
即EG的长为.
21.证明:连接BC、AD,如图:
∵BF=DE,
∴BF﹣EF=DE﹣EF
即BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AB=CD,∠ABE=∠CDF,
∴AB∥CD,
∴四边形ABCD是平行四边形,
∴AC与BD互相平分.
22.证明:连接AD、BC,如图所示:
∵AB∥CD,
∴∠BAF=∠DCE,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(ASA),
∴AB=CD,
又∵AB∥CD,
∴四边形ABCD是平行四边形,
∴AC与BD互相平分.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠ABC=∠BCF,
∵E为BC中点,
∴BE=CE,
在△ABE和△FCE中,
,
∴△ABE≌△FCE;
(2)当AD=AF时,四边形ABFC是矩形,
理由:∵AD=AF,四边形ABFC为平行四边形,
∴AE=AF=AD,
∵四边形ABCD是平行四边形,
∴BC=AD,
∵AE=BC,
∴AF=BC,
∴四边形ABFC为矩形(对角线相等的平行四边形是矩形).
24.证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,AD=BC,
∵DE、BF分别是∠ADC和∠ABC的角平分线,
∴∠ADE=∠CDE,∠CBF=∠ABF,
∵CD∥AB,
∴∠AED=∠CDE,∠CFB=∠ABF,
∴∠AED=∠ADE,∠CFB=∠CBF,
∴AE=AD,CF=CB,
∴AE=CF,
∴AB﹣AE=CD﹣CF 即BE=DF,
∵DF∥BE,
∴四边形DEBF是平行四边形.
∴BD、EF互相平分.
25.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠BAD=∠BCD
∴∠ABE=∠CDF,
∵AE平分∠BAD,CF平分∠BCD,
∴∠BAE=∠DCF,
∴△ABE≌△CDF(ASA),
∴AE=CF;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,∠BAD+∠ABC=180°,
∵∠ABC=70°,
∴∠BAD=110°,
∵AM平分∠BAD,AD∥BC,
∴∠AMB=∠DAM=55°.
26.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠BAD=∠BCD.
∴∠ADB=∠CBD.
∵∠BAD、∠BCD的平分线分别交对角线BD于点E、F,
∴∠EAD=∠BAD,∠FCB=∠BCD,
∴∠EAD=∠FCB.
在△AED和△CFB中,
,
∴△AED≌△CFB(ASA),
∴∠AED=∠CFB,
∴AE∥CF.
27.证明:(1)∵AB∥DE,
∴∠B=∠DEF,
∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);
(2)由(1)得:△ABC≌△DEF,
∴AC=DF,∠ACB=∠F,
∴AC∥DF,
∴四边形ACFD是平行四边形.
28.证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA+AE=OC+CF,
即OE=OF,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(SAS),
∴DE=BF.
29.(1)证明∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FDE=∠C,∠F=∠CBE,
∵E是CD边上的中点,
∴DE=CE,
在△BCE和△FDE中,
,
∴△BCE≌△FDE(AAS);
(2)解:由(1)得△BCE≌△FDE,
∴BC=DF=3,
∵E是CD边上的中点,
∴CD=2DE=4,
∴ ABCD的周长为:2(BC+CD)=14.
30.证明:连接BF、DE,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F分别是OA、OC的中点,
∴OE=OA,OF=OC,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴BE=DF.
1.如图,已知 ABCD,E为BC边上的垂直平分线,BC=FC=2AB,且∠ABD=90°.
(1)求证:△ABD≌△CEF;
(2)连接AF,请判断四边形ABDF的形状,并说明理由.
2.如图,在△NMB中,BM=8,点A,C,D分别在边MB,BN,MN上,DA∥NB,DC∥MB,∠NDC=∠MDA.求四边形ABCD的周长.
3.如图,在平行四边形ABCD中,点E、F分别在边BC和AD上,且BE=DF.
求证:AE∥CF.
4.如图,四边形ABCD中,AB∥CD,AB=CD.AD与CB有什么关系?证明你的结论.
5.已知:如图,在 ABCD中,E,F分别为BC和AD上的点,BD和EF相交于点O,且OE=OF.求证:四边形AECF为平行四边形.
6.如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,求BD的长.
7.如图,AB,CD相交于点E且互相平分,F是BD延长线上一点,若∠FAC=2∠BAC,求证:AC+DF=AF.
8.如图,四边形ABCD是平行四边形,E,F是对角线AC的三等分点,连接BE,DF.证明:BE=DF.
9.如图,在平行四边形ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:△BOE≌△COD;
(2)若BC平分∠DBE,请判断并证明四边形BECD的形状.
10.已知:如图,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:(1)△AFD≌△CEB;
(2)四边形AECF是平行四边形.
11.如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,且AD=AF.
(1)判断四边形ABFC的形状并证明;
(2)若AB=3,∠ABC=60°,求EF的长.
12.如图,在平行四边形ABCD中,点F是AD中点,连接CF并延长交BA的延长线于点E.
(1)求证:AB=AE.
(2)若BC=2AE,∠E=31°,求∠DAB的度数.
13.已知: ABCD中,E、F是对角线BD上两点,连接AE、CF,若∠BAE=∠DCF.求证:AE=CF.
14.如图,E、F是 ABCD对角线AC上的两点,AF=CE.求证:BE=DF.
15.如图,将 ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF.求证:四边形AECF是平行四边形.
16.如图,平行四边形ABCD的对角线交于点E,若BC=4,BD=10,AC=6.
(1)求证:∠ACB=90°;
(2)求CD的长.
17.如图,F、C是线段AD上的两点,AB∥DE,BC∥EF,AF=DC,连结AE、BD,求证:四边形ABDE是平行四边形.
18.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O的直线EF分别交AD于点E,交BC于点F,求证:AE=CF.
19.如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=5,AC=8,求四边形AECD的面积.
20.如图,在 ABCD中,点E在边BC上,点F在边AD的延长线上,且∠ADB=∠F,EF与CD交于点G.
(1)求证:四边形BDFE是平行四边形;
(2)若AD=10,BE=4,FG=5,求EG的长.
21.已知:如图,点E,F在BD上,且AE=CF,BF=DE,∠AEB=∠CFD.求证:AC与BD互相平分.
22.如图,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,AB∥CD.求证:AC与BD互相平分.
23.如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC.
(1)求证:△ABE≌△FCE;
(2)若AD=AF,判断四边形ABFC是什么特殊四边形,并说明理由.
24.如图,在平行四边形ABCD中,DE,BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.求证:BD、EF互相平分.
25.如图,在 ABCD中,AE平分∠BAD交BD于点E,交BC于点M,CF平分∠BCD交BD于点F.
(1)求证:AE=CF;
(2)若∠ABC=70°,求∠AMB的度数.
26.如图,BD是 ABCD的对角线,∠BAD的平分线交BD于点E,∠BCD的平分线交BD于点F.求证:AE∥CF.
27.如图,点B,E,C,F在一条直线上,AB=DE,AB∥DE,BE=CF.
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形ACFD是平行四边形.
28.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在CA和AC的延长线上,且AE=CF,连接DE,BF.求证:DE=BF.
29.如图,在 ABCD中,E是CD边上的中点,AD,BE的延长线相交于点F.
(1)求证:△BCE≌△FDE.
(2)若DF=3,DE=2,求 ABCD的周长.
30.如图, ABCD对角线AC,BD相交于点O,E,F分别是OA,OC的中点,连接BE、DF.求证:BE=DF.
参考答案
1.(1)证明:∵四边形ABCD是平行四边形,
∴BC=AD,AB=CD,
∵E为BC边上的垂直平分线,
∴BC=2EC=2BE,∠FEC=90°,
∵BC=FC=2AB,
∴EC=AB=CD,BC=BF=FC,
∴△BCF是等边三角形,
∴AD=FC,
∴∠ABD=∠FEC=90°,
在Rt△ABD和Rt△CEF中,
,
∴Rt△ABD≌Rt△CEF(HL);
(2)解:四边形ABDF是矩形,理由如下:
∵△BCF是等边三角形,
∴BC=FC=2AB=2CD,
∴FD=CD=AB,
∵AB∥CD,
∴四边形ABDF是平行四边形,
∵∠ABD=90°,
∴四边形ABDF是矩形.
2.解:∵DA∥NB,DC∥MB,
∴∠NDC=∠M,四边形ABCD为平行四边形,
∴DC=AB,AD=BC,
∵∠NDC=∠MDA.
∴AD=AM,
∴四边形ABCD的周长=AB+BC+CD+AD=2AM+2AB=2BM=2×8=16.
3.证明:四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵BE=DF,
∴AD﹣DF=BC﹣BE,
即AF=CE,
∵AF∥CE,
∴四边形AECF是平行四边形,
∴AE∥CF.
4.解:AD=BC且AD∥BC.
证明:∵AB∥CD,
∴∠ABD=∠CDB.
在△ABD与△CDB中,
,
∴△ABD≌△CDB(SAS).
∴AD=BC,∠ADB=∠CBD.
∴AD∥BC.
5.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ODF=∠OBE,
在△DOF和△BOE中,
,
∴△DOF≌△BOE(AAS),
∴DF=BE,
∴AD﹣DF=BC﹣BE,
即AF=EC,
∴四边形AECF为平行四边形.
6.解:∵ ABCD的对角线AC与BD相交于点O,
∴BO=DO,OA=OC,BC=AD=5,
∵AB⊥AC,AB=3,
∴AC==4,
∴OA=2,
∴BO==,
∴BD=2BO=2.
故BD的长为2.
7.证明:连接AD、BC,
∵AB,CD相交于点E且互相平分,
∴四边形ACBD是平行四边形,
∴AC=BC,AC∥BC,
∴∠BAC=∠ABF,
∵∠FAC=2∠BAC,
∴∠FAB=∠BAC,
∴∠ABF=∠FAB,
∴AF=BF,
∵AC+DF=BD+DF=BF,
∴AC+DF=AF.
8.证明:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∴∠BAC=∠DCA,
∵E,F是对角线AC的三等分点,
∴AE=CF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
9.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,
,
∴△BOE≌△COD(AAS);
(2)解:四边形BECD是菱形;
证明:∵△BOE≌△COD,
∴OE=OD,BO=CO,
∴四边形BECD是平行四边形,
∵AE∥CD,
∴∠BCD=∠CBE,
∵BC平分∠DBE,
∴∠DBC=∠CBE,
∴∠DBC=∠DCB,
∴BD=DC,
∴四边形BECD是菱形.
10.证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D,
又∵E,F分别是AB,CD的中点,
∴AE=BE=AB,CF=DF=CD,
∴BE=DF,AE=CF,
在△AFD和△CEB中,
,
∴△AFD≌△CEB(SAS);
(2)由(1)知AE=CF,△AFD≌△CEB,
∴AF=CE,
∴四边形AECF是平行四边形.
11.解:(1)四边形ABFC是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
∵E为BC的中点,
∴EB=EC,
在△ABE和△FCE中,
,
∴△ABE≌△FCE(AAS),
∴AB=CF.
∵AB∥CF,
∴四边形ABFC是平行四边形,
∵AD=BC,AD=AF,
∴BC=AF,
∴四边形ABFC是矩形.
(2)∵四边形ABFC是矩形,
∴BC=AF,AF=EF,BE=CE,
∴AE=BE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴AB=AE=3,
∴EF=3.
12.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,BC=AD,
∴∠E=∠DCF,
∵点F是AD中点,
∴AF=DF,
∵∠EFA=∠CFD,
∴△AFE≌△DFC(AAS),
∴CD=AE,
∴AB=AE;
(2)解:由(1)可得AF=DF,BC=AD,
∵BC=2AE,
∴AE=AF,
∵∠E=31°,
∴∠AFE=∠E=31°,
∴∠DAB=2∠E=62°.
13.证明∵四边形ABCD为平行四边形
∴AB∥CD,AB=CD
∴∠ABD=∠CDB
∵∠BAE=∠DCF,CD=AB,∠ABD=∠BDC
∴△ABE≌△CDF
∴AE=CF
14.证明:∵AF=CE.
∴AE=CF,
∵在 ABCD中,AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
15.证明:连接AC,设AC与BD交于点O.如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵BE=DF,
∴OE=OF.
∴四边形AECF是平行四边形.
16.(1)证明:∵四边形ABCD是平行四边形,BD=10,AC=6,
∴BE=5,CE=3,
∵32+42=52,
即BE2=CE2+BC2,
∴△BEC是直角三角形,
即∠ACB=90°;
(2)解:∵四边形ABCD是平行四边形,∠ACB=90°,
∴AD∥BC,AD=BC=4,
∴∠CAD=90°,
在Rt△ACD中,由勾股定理得,CD=.
17.证明:∵AF=DC,
∴AF+FC=DC+FC,
∴AC=DF,
∵AB∥DE,
∴∠BAC=∠EDF,
∵BC∥EF,
∴∠ACB=∠EFD,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AB=DE,
又∵AB∥DE,
∴四边形ABDE是平行四边形.
18.证明:∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
∵,
∴△AOE≌△COF(ASA)
∴AE=CF.
19.(1)证明:在△AOE和△COD中,
,
∴△AOE≌△COD(ASA),
∴OD=OE,
又∵AO=CO,
∴四边形AECD是平行四边形;
(2)解:∵AB=BC,AO=CO,
∴OB⊥AC,
∴平行四边形AECD是菱形,
∵AC=8,
∴CO=AC=4,
在Rt△COD中,由勾股定理得:OD===3,
∴DE=2OD=6,
∴菱形AECD的面积=AC×DE=×8×6=24.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠ADB=∠F,
∴BD∥EF,
∴四边形BDFE是平行四边形;
(2)解:由(1)得:四边形BDFE是平行四边形,
∴DF=BE=4,
∵四边形ABCD是平行四边形,
∴BC=AD=10,
∴CE=BC﹣BE=10﹣4=6,AD∥BC,
∴△CEG∽△DFG,
∴=,
即=,
解得:EG=,
即EG的长为.
21.证明:连接BC、AD,如图:
∵BF=DE,
∴BF﹣EF=DE﹣EF
即BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AB=CD,∠ABE=∠CDF,
∴AB∥CD,
∴四边形ABCD是平行四边形,
∴AC与BD互相平分.
22.证明:连接AD、BC,如图所示:
∵AB∥CD,
∴∠BAF=∠DCE,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(ASA),
∴AB=CD,
又∵AB∥CD,
∴四边形ABCD是平行四边形,
∴AC与BD互相平分.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠ABC=∠BCF,
∵E为BC中点,
∴BE=CE,
在△ABE和△FCE中,
,
∴△ABE≌△FCE;
(2)当AD=AF时,四边形ABFC是矩形,
理由:∵AD=AF,四边形ABFC为平行四边形,
∴AE=AF=AD,
∵四边形ABCD是平行四边形,
∴BC=AD,
∵AE=BC,
∴AF=BC,
∴四边形ABFC为矩形(对角线相等的平行四边形是矩形).
24.证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,AD=BC,
∵DE、BF分别是∠ADC和∠ABC的角平分线,
∴∠ADE=∠CDE,∠CBF=∠ABF,
∵CD∥AB,
∴∠AED=∠CDE,∠CFB=∠ABF,
∴∠AED=∠ADE,∠CFB=∠CBF,
∴AE=AD,CF=CB,
∴AE=CF,
∴AB﹣AE=CD﹣CF 即BE=DF,
∵DF∥BE,
∴四边形DEBF是平行四边形.
∴BD、EF互相平分.
25.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠BAD=∠BCD
∴∠ABE=∠CDF,
∵AE平分∠BAD,CF平分∠BCD,
∴∠BAE=∠DCF,
∴△ABE≌△CDF(ASA),
∴AE=CF;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,∠BAD+∠ABC=180°,
∵∠ABC=70°,
∴∠BAD=110°,
∵AM平分∠BAD,AD∥BC,
∴∠AMB=∠DAM=55°.
26.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠BAD=∠BCD.
∴∠ADB=∠CBD.
∵∠BAD、∠BCD的平分线分别交对角线BD于点E、F,
∴∠EAD=∠BAD,∠FCB=∠BCD,
∴∠EAD=∠FCB.
在△AED和△CFB中,
,
∴△AED≌△CFB(ASA),
∴∠AED=∠CFB,
∴AE∥CF.
27.证明:(1)∵AB∥DE,
∴∠B=∠DEF,
∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);
(2)由(1)得:△ABC≌△DEF,
∴AC=DF,∠ACB=∠F,
∴AC∥DF,
∴四边形ACFD是平行四边形.
28.证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA+AE=OC+CF,
即OE=OF,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(SAS),
∴DE=BF.
29.(1)证明∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FDE=∠C,∠F=∠CBE,
∵E是CD边上的中点,
∴DE=CE,
在△BCE和△FDE中,
,
∴△BCE≌△FDE(AAS);
(2)解:由(1)得△BCE≌△FDE,
∴BC=DF=3,
∵E是CD边上的中点,
∴CD=2DE=4,
∴ ABCD的周长为:2(BC+CD)=14.
30.证明:连接BF、DE,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F分别是OA、OC的中点,
∴OE=OA,OF=OC,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴BE=DF.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
