人教版七年级数学下册 7.2.2用坐标表示平移 同步练习题(word版、含答案)
文档属性
| 名称 | 人教版七年级数学下册 7.2.2用坐标表示平移 同步练习题(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 209.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 00:00:00 | ||
图片预览

文档简介
用坐标表示平移
一、单选题
在平面直角坐标系中,将点 A(﹣1, ﹣2)向右平移 3 个单位长度得到点 B,则点 B 关于 x 轴的对称点 B′的坐标为( )
A.(﹣3,﹣2) B.(2,2) C.(﹣2,2) D.(2,﹣2)
在平面直角坐标系中,将点 A(1,﹣2)向上平移 3 个单位长度,再向左平移 2 个单位长度,得到点 A′,则点 A′的坐标是( )
A.(﹣1,1) B.(﹣1,﹣2) C.(﹣1,2) D.(1,2)
已知点 A的坐标为(1,3),点 B的坐标为(2,1).将线段 AB沿某一方向平移后,点A的对应点的坐标为(–2,1),则点 B的对应点的坐标为
A.(5,3) B.(–1,–2)
C.(–1,–1) D.(0,–1)
已知三角形的三个顶点坐标分别为(-2,1),(2,3),(-3,-1),把这个三角形运动 到一个确定位置,在下列各点的坐标中,是经过平移得到的是( ) A.(0,3),(0,1),(-1,-1) B.(-3,2),(3,2),(-4,0)
C.(1,-2),(3,2),(-1,-3) D.(-1,3),(3,5),(-2,1) 5.将某图形中所有点的横坐标都减去 2,纵坐标不变,则该图形( ) A.向上平移 2 个单位 B.向下平移 2 个单位
C.向右平移 2 个单位 D.向左平移 2 个单位
如图,已知点 , 的坐标分别为(3,0),(0,4),将线段 平移到 ,若点 的对应点 的坐标为(4,2),则 的对应点 的坐标为( ).
A.(1,6) B.(2,5) C.(6,1) D.(4,6)
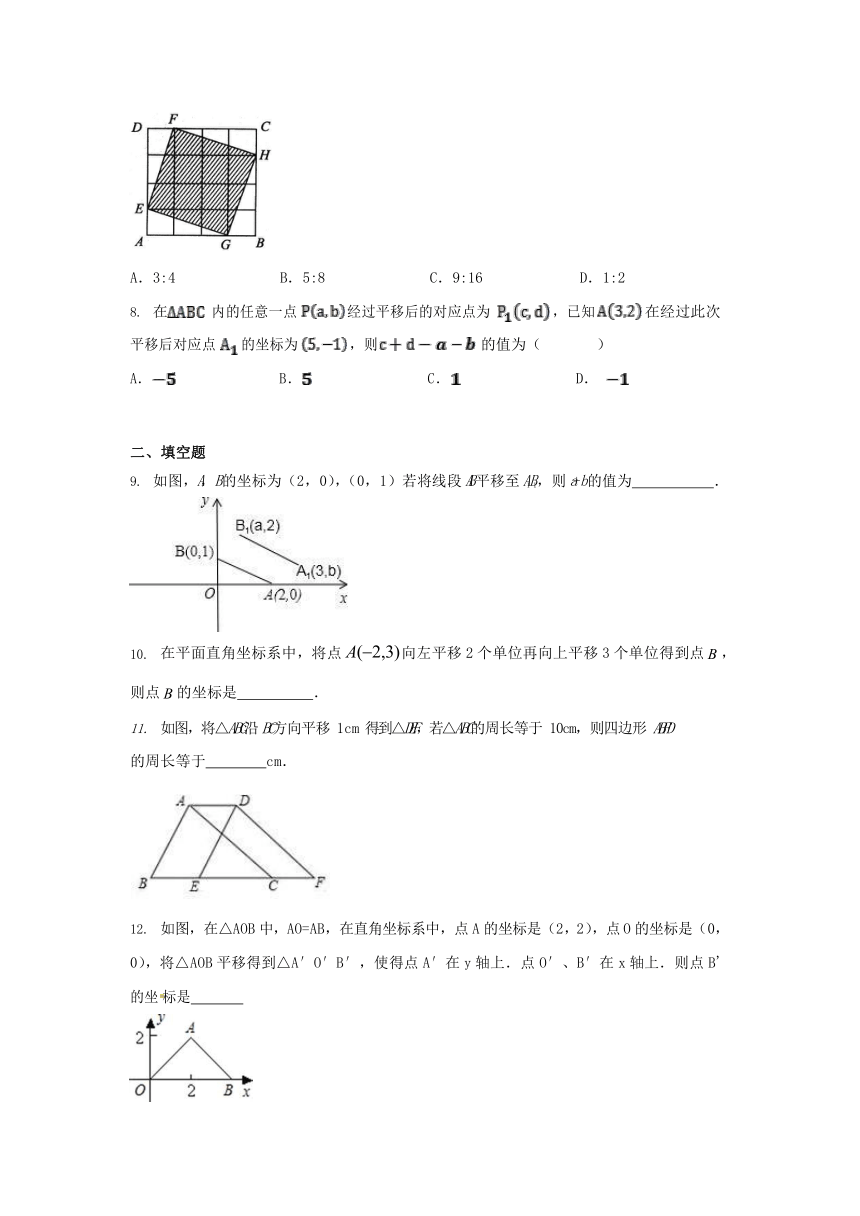
如图所示,在一个由 4×4 个小正方形组成的正方形网格中,把线段 EF 向右平移 3 个单位,向下平移 1 个单位得到线段 GH,则阴影部分面积与正方形 ABCD 的面积比是( )
A.3:4 B.5:8 C.9:16 D.1:2
在 内的任意一点 经过平移后的对应点为 ,已知 在经过此次平移后对应点 的坐标为 ,则 的值为( )
A. B. C. D.
二、填空题
如图,A,B的坐标为(2,0),(0,1)若将线段 AB平移至 A1B1,则 a+b的值为 .
在平面直角坐标系中,将点 A( 2,3) 向左平移 2 个单位再向上平移 3 个单位得到点 B , 则点 B 的坐标是 .
如图,将△ABC沿 BC方向平移 1cm 得到△DEF,若△ABC的周长等于 10cm,则四边形 ABFD
的周长等于 cm.
如图,在△AOB 中,AO=AB,在直角坐标系中,点 A 的坐标是(2,2),点 O 的坐标是(0,
0),将△AOB 平移得到△A′O′B′,使得点 A′在 y 轴上.点 O′、B′在 x 轴上.则点 B'的坐标是
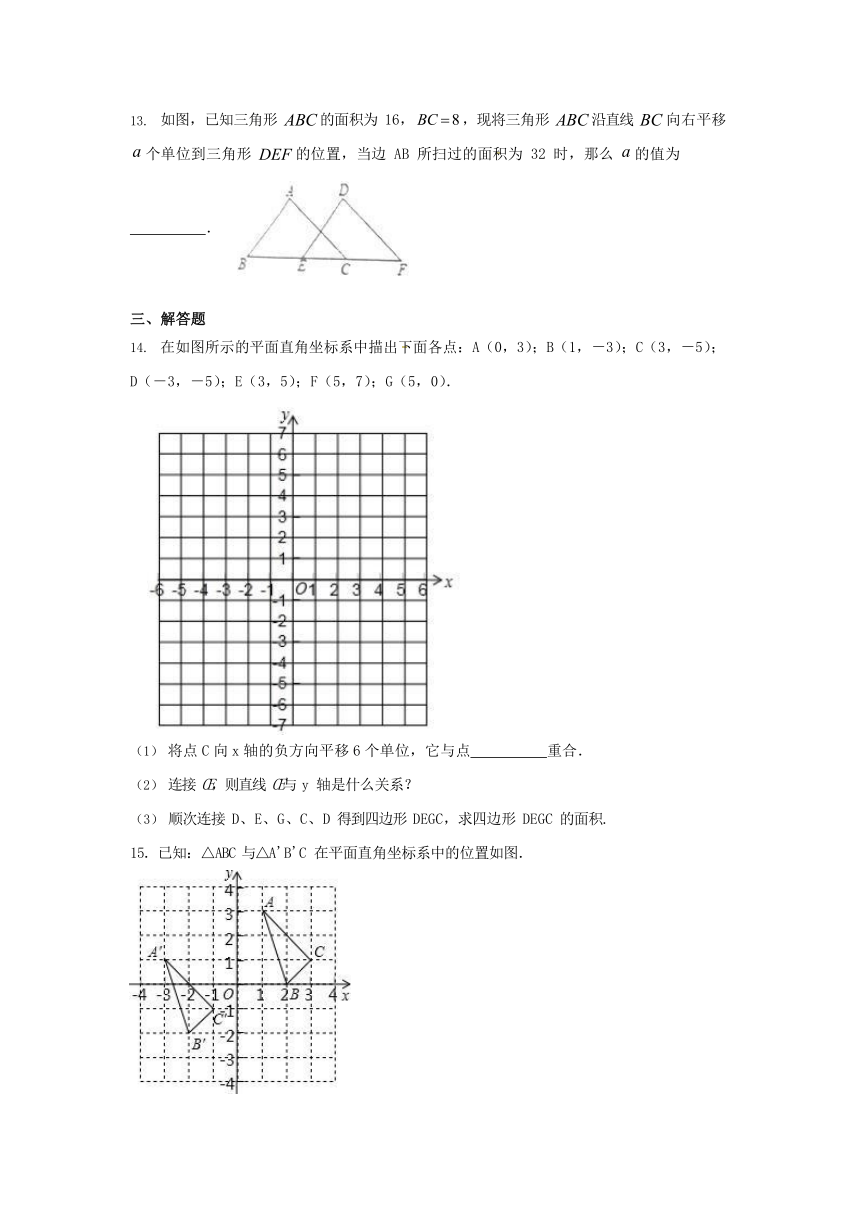
如图,已知三角形 ABC 的面积为 16, BC 8 ,现将三角形 ABC 沿直线 BC 向右平移
a 个单位到三角形 DEF 的位置,当边 AB 所扫过的面积为 32 时,那么 a 的值为
.
三、解答题
在如图所示的平面直角坐标系中描出下面各点:A(0,3);B(1,-3);C(3,-5); D(-3,-5);E(3,5);F(5,7);G(5,0).
将点 C 向 x 轴的负方向平移 6 个单位,它与点 重合.
连接 CE,则直线 CE与 y 轴是什么关系?
顺次连接 D、E、G、C、D 得到四边形 DEGC,求四边形 DEGC 的面积. 15.已知:△ABC 与△A'B'C 在平面直角坐标系中的位置如图.
分别写出 B、B'的坐标:B ;B′ ;
若点 P(a,b)是△ABC 内部一点,则平移后△A'B'C 内的对应点 P′的坐标为 ;
求△ABC 的面积.
如图,方格纸中每个小格子的边长均为1个单位长度, ABC 的三个顶点和点 P 都在方格纸的格点上,
若将 ABC 平移,使点 P 恰好落在平移后得到的 A B C 的内部,则符合要求的三角形能画出 个,请在方格纸中画出符合要求的一个三角形;
在(1)的条件下,若连接对应点 BB 、CC ,则这两条线段的位置关系是 ;
画一条直线l ,将 ABC 分成两个面积相等的三角形.
如图,长方形 OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐 标为(0,6),点 B在第一象限内,点 P从原点 O出发,以每秒 2 个单位长度的速度沿着 O
﹣A﹣B﹣C﹣O的路线移动(即沿长方形移动一周).
写出 B点的坐标;
当点 P移动 3 秒时,求三角形 OAP的面积;
在移动过程中,当点 P到 x轴距离为 4 个单位长度时,求点 P移动的时间
答案1.B
2.A
3.C
4.D
5.D
6.A
7.B
8.D
9.2
10. ( 4, 6)
11.12
12.(2,0)
13.8
14.(1) 易知 C 向 x 负半轴移动 6 个单位,即往左边移动 6 个单位,与 D 重叠.
连接 CE,因为两点坐标 x 值相等,故 CE 垂直于 x 轴交于 H 点,平行于 y 轴
四边形 DEGC 面积=S△EDC+S△
GEC= 1 DC EC 1 EC GH 1 6 10 1 10 2 =40
2 2 2 2
15.解:(1)由图知点 B′的坐标为(2,0)、点 B 坐标为(-2,-2),故答案为:(2,0)、(-2,-2);
由图知△ABC 向左平移 4 个单位,再向下平移 2 个单位可得到△A'B'C′, 则平移后△A'B'C 内的对应点 P′的坐标为(a-4,b-2),
故答案为:(a-4,b-2);
1
△ABC 的面积为 2×3-
2
1
×1×3-
2
1
×1×1-
2
×2×2=2.
解:(1)∵△ABC 内部有 10 个格点,
∴使点 P 恰好落在平移后得到的△A'B'C'的内部,则符合要求的格点三角形能画出 10 个, 如图所示,△A'B'C'即为所求(答案不唯一);
故答案为:10;
连接对应点 BB'、CC',则这两条线段的位置关系是平行或在同一条直线上; 故答案为:平行或在同一条直线上;
如图所示,直线 l 即为所求(答案不唯一).
解:(1)根据长方形的性质,可得 AB与 y轴平行,BC与 x轴平行; 故 B的坐标为(4,6);
(2)∵A(4,0)、C(0,6),
∴OA=4,OC=6.
∵3×2=6>4,
∴点 P在线段 AB上.
∴PA=2.
1
∴S△OAP=
2
1
OA×PA=
2
×4×2=4.
(3)∵OC=AB=6>4,∴点 P在 AB上或 OC上.
当点 P在 AB上时,PA=4,
1
此时点 P移动路程为 4+4=8,时间为
2
当点 P在 OC上时,OP=4,
×8=4.
1
此时点 P移动路程为 2(4+6)﹣4=16,时间为
2
∴点 P移动的时间为 4 秒或 8 秒
×16=8.
一、单选题
在平面直角坐标系中,将点 A(﹣1, ﹣2)向右平移 3 个单位长度得到点 B,则点 B 关于 x 轴的对称点 B′的坐标为( )
A.(﹣3,﹣2) B.(2,2) C.(﹣2,2) D.(2,﹣2)
在平面直角坐标系中,将点 A(1,﹣2)向上平移 3 个单位长度,再向左平移 2 个单位长度,得到点 A′,则点 A′的坐标是( )
A.(﹣1,1) B.(﹣1,﹣2) C.(﹣1,2) D.(1,2)
已知点 A的坐标为(1,3),点 B的坐标为(2,1).将线段 AB沿某一方向平移后,点A的对应点的坐标为(–2,1),则点 B的对应点的坐标为
A.(5,3) B.(–1,–2)
C.(–1,–1) D.(0,–1)
已知三角形的三个顶点坐标分别为(-2,1),(2,3),(-3,-1),把这个三角形运动 到一个确定位置,在下列各点的坐标中,是经过平移得到的是( ) A.(0,3),(0,1),(-1,-1) B.(-3,2),(3,2),(-4,0)
C.(1,-2),(3,2),(-1,-3) D.(-1,3),(3,5),(-2,1) 5.将某图形中所有点的横坐标都减去 2,纵坐标不变,则该图形( ) A.向上平移 2 个单位 B.向下平移 2 个单位
C.向右平移 2 个单位 D.向左平移 2 个单位
如图,已知点 , 的坐标分别为(3,0),(0,4),将线段 平移到 ,若点 的对应点 的坐标为(4,2),则 的对应点 的坐标为( ).
A.(1,6) B.(2,5) C.(6,1) D.(4,6)
如图所示,在一个由 4×4 个小正方形组成的正方形网格中,把线段 EF 向右平移 3 个单位,向下平移 1 个单位得到线段 GH,则阴影部分面积与正方形 ABCD 的面积比是( )
A.3:4 B.5:8 C.9:16 D.1:2
在 内的任意一点 经过平移后的对应点为 ,已知 在经过此次平移后对应点 的坐标为 ,则 的值为( )
A. B. C. D.
二、填空题
如图,A,B的坐标为(2,0),(0,1)若将线段 AB平移至 A1B1,则 a+b的值为 .
在平面直角坐标系中,将点 A( 2,3) 向左平移 2 个单位再向上平移 3 个单位得到点 B , 则点 B 的坐标是 .
如图,将△ABC沿 BC方向平移 1cm 得到△DEF,若△ABC的周长等于 10cm,则四边形 ABFD
的周长等于 cm.
如图,在△AOB 中,AO=AB,在直角坐标系中,点 A 的坐标是(2,2),点 O 的坐标是(0,
0),将△AOB 平移得到△A′O′B′,使得点 A′在 y 轴上.点 O′、B′在 x 轴上.则点 B'的坐标是
如图,已知三角形 ABC 的面积为 16, BC 8 ,现将三角形 ABC 沿直线 BC 向右平移
a 个单位到三角形 DEF 的位置,当边 AB 所扫过的面积为 32 时,那么 a 的值为
.
三、解答题
在如图所示的平面直角坐标系中描出下面各点:A(0,3);B(1,-3);C(3,-5); D(-3,-5);E(3,5);F(5,7);G(5,0).
将点 C 向 x 轴的负方向平移 6 个单位,它与点 重合.
连接 CE,则直线 CE与 y 轴是什么关系?
顺次连接 D、E、G、C、D 得到四边形 DEGC,求四边形 DEGC 的面积. 15.已知:△ABC 与△A'B'C 在平面直角坐标系中的位置如图.
分别写出 B、B'的坐标:B ;B′ ;
若点 P(a,b)是△ABC 内部一点,则平移后△A'B'C 内的对应点 P′的坐标为 ;
求△ABC 的面积.
如图,方格纸中每个小格子的边长均为1个单位长度, ABC 的三个顶点和点 P 都在方格纸的格点上,
若将 ABC 平移,使点 P 恰好落在平移后得到的 A B C 的内部,则符合要求的三角形能画出 个,请在方格纸中画出符合要求的一个三角形;
在(1)的条件下,若连接对应点 BB 、CC ,则这两条线段的位置关系是 ;
画一条直线l ,将 ABC 分成两个面积相等的三角形.
如图,长方形 OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐 标为(0,6),点 B在第一象限内,点 P从原点 O出发,以每秒 2 个单位长度的速度沿着 O
﹣A﹣B﹣C﹣O的路线移动(即沿长方形移动一周).
写出 B点的坐标;
当点 P移动 3 秒时,求三角形 OAP的面积;
在移动过程中,当点 P到 x轴距离为 4 个单位长度时,求点 P移动的时间
答案1.B
2.A
3.C
4.D
5.D
6.A
7.B
8.D
9.2
10. ( 4, 6)
11.12
12.(2,0)
13.8
14.(1) 易知 C 向 x 负半轴移动 6 个单位,即往左边移动 6 个单位,与 D 重叠.
连接 CE,因为两点坐标 x 值相等,故 CE 垂直于 x 轴交于 H 点,平行于 y 轴
四边形 DEGC 面积=S△EDC+S△
GEC= 1 DC EC 1 EC GH 1 6 10 1 10 2 =40
2 2 2 2
15.解:(1)由图知点 B′的坐标为(2,0)、点 B 坐标为(-2,-2),故答案为:(2,0)、(-2,-2);
由图知△ABC 向左平移 4 个单位,再向下平移 2 个单位可得到△A'B'C′, 则平移后△A'B'C 内的对应点 P′的坐标为(a-4,b-2),
故答案为:(a-4,b-2);
1
△ABC 的面积为 2×3-
2
1
×1×3-
2
1
×1×1-
2
×2×2=2.
解:(1)∵△ABC 内部有 10 个格点,
∴使点 P 恰好落在平移后得到的△A'B'C'的内部,则符合要求的格点三角形能画出 10 个, 如图所示,△A'B'C'即为所求(答案不唯一);
故答案为:10;
连接对应点 BB'、CC',则这两条线段的位置关系是平行或在同一条直线上; 故答案为:平行或在同一条直线上;
如图所示,直线 l 即为所求(答案不唯一).
解:(1)根据长方形的性质,可得 AB与 y轴平行,BC与 x轴平行; 故 B的坐标为(4,6);
(2)∵A(4,0)、C(0,6),
∴OA=4,OC=6.
∵3×2=6>4,
∴点 P在线段 AB上.
∴PA=2.
1
∴S△OAP=
2
1
OA×PA=
2
×4×2=4.
(3)∵OC=AB=6>4,∴点 P在 AB上或 OC上.
当点 P在 AB上时,PA=4,
1
此时点 P移动路程为 4+4=8,时间为
2
当点 P在 OC上时,OP=4,
×8=4.
1
此时点 P移动路程为 2(4+6)﹣4=16,时间为
2
∴点 P移动的时间为 4 秒或 8 秒
×16=8.
