2021-2022学年苏科版八年级数学下册9.3.2平行四边形的判定 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学下册9.3.2平行四边形的判定 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 311.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
9.3平行四边形(二)
复习提问:
1.什么平行四边形?
2.平行四边形的性质:
两组对边分别平行的四边形是平行四边形
①
②
③
④
对边相等
对角相等
对角线互相平分
是中心对称图形
自主预习
类比平行线的性质和判定的关系,
你能猜想出平行四边形的判定方法吗?
什么样的四边形是平行四边形
边组合 角组合 ;
两条对角线 .
你会论证吗?
目标定向
1.探索并掌握平行四边形的判定条件;
2.经历平行四边形判定条件的探索过程,发展学生合情的说理能力,感受“性质”与“判定”之间的内在联系;
3.在丰富的活动中,发展学生有条理的思考,培养学生的探索意识和创新能力.
操作:在方格纸上画两条互相平行且相等的线段
AD、BC,连接AB、CD.检验线段AB与CD是否
互相平行.
思考:你能说明所画四边形ABCD是平行四边形吗?
合作探究1
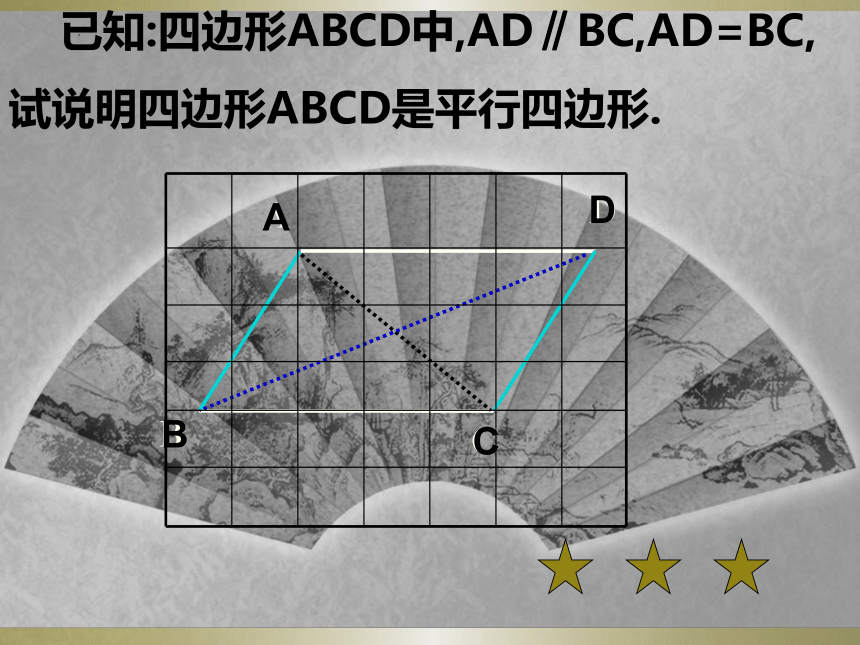
已知:四边形ABCD中,AD∥BC,AD=BC,
试说明四边形ABCD是平行四边形.
B
C
A
D
A
D
B
C
A
B
C
D
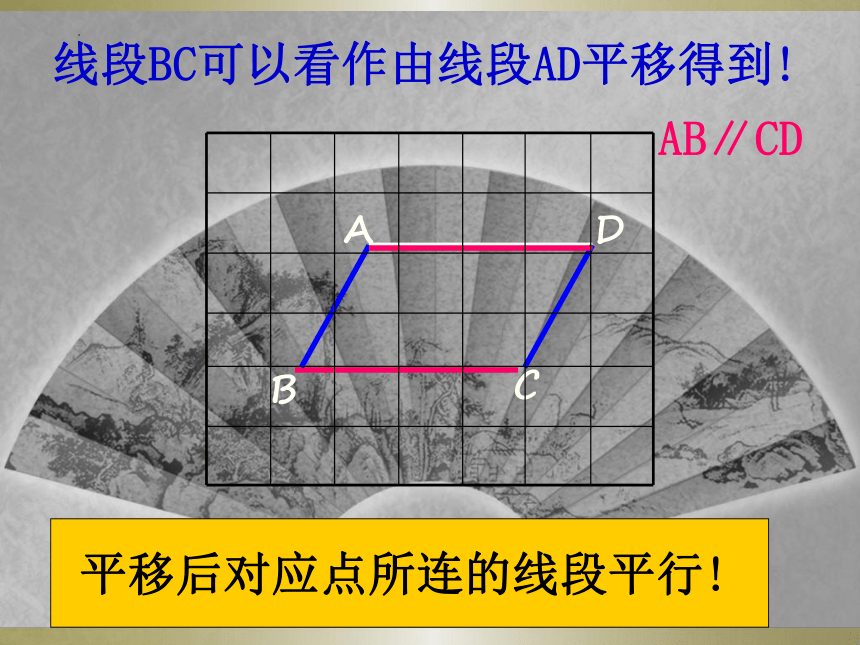
线段BC可以看作由线段AD平移得到!
AB∥CD
平移后对应点所连的线段平行!
A
D
C
B
结论
∵AD∥BC且AD=BC
∴四边形ABCD是平行四边形.
(一组对边平行且相等的四边形是平行四边形).
一组对边平行且相等的四边形是平行四边形.
几何语言
例1:如图 ,在平行四边形ABCD中,E,F分别是
AD,BC的中点.
求证:四边形EBFD是平行四边形.
灵活运用:
变式:如图 ,在平行四边形ABCD中,E,F分别是
AD,BC上的一点,且AE=CF。
求证:四边形EBFD是平行四边形.
例1:如图 ,在平行四边形ABCD中,E,F分别是
AD,BC的中点.
求证:四边形EBFD是平行四边形.
灵活运用:
变式:如图 ,在平行四边形ABCD中,E,F分别是
AD,BC上的一点,且AE=CF。
求证:四边形EBFD是平行四边形.
在四边形ABCD中,AB=CD,AD=BC.
四边形ABCD是平行四边形吗?证明你的结论.
A
D
C
B
合作探究2
A
D
C
B
两组对边分别相等的四边形是平行四边形.
∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
结论
几何语言
(两组对边分别相等的四边形是平行四边形)
如图,□ABCD中,AF=CH,DE=BG,
求证: EG和HF互相平分.
灵活运用:
通过本节课的学习和探索,你有哪些收获
小结与思考
一组对边平行且相等
两组对边分别平行
两组对边分别相等
的四边形是平行四边形.
2、平行四边形的判别方法:
1、从平移、中心对称、说理等不同角度探索了平行四边形的判别方法.
判断
(1)一组对边平行且另一组对边相等的四边形是
平行四边形; ( )
(2)两组对角都相等的四边形是平行四边形 ( )
(3)一组对边平行且一组对角相等的四边形是平行
边形; ( )
(4)一组对边平行,一组邻角互补的四边形是平行
四边形; ( )
(5)两组邻角互补的四边形是平行四边形. ( )
×
√
√
×
×
检测反馈
1.如图,在□ABCD中,AE⊥BD,CF⊥BD,垂足分别是E、F,求证:四边形AECF是平行四边形.
整合提升
2.如图,在□ABCD中,点E、F分别在AD、BC上,且AE=CF,AE、BE相交于点G,CE、DF相交于点H.
求证:EF与GH互相平分。
9.3平行四边形(二)
复习提问:
1.什么平行四边形?
2.平行四边形的性质:
两组对边分别平行的四边形是平行四边形
①
②
③
④
对边相等
对角相等
对角线互相平分
是中心对称图形
自主预习
类比平行线的性质和判定的关系,
你能猜想出平行四边形的判定方法吗?
什么样的四边形是平行四边形
边组合 角组合 ;
两条对角线 .
你会论证吗?
目标定向
1.探索并掌握平行四边形的判定条件;
2.经历平行四边形判定条件的探索过程,发展学生合情的说理能力,感受“性质”与“判定”之间的内在联系;
3.在丰富的活动中,发展学生有条理的思考,培养学生的探索意识和创新能力.
操作:在方格纸上画两条互相平行且相等的线段
AD、BC,连接AB、CD.检验线段AB与CD是否
互相平行.
思考:你能说明所画四边形ABCD是平行四边形吗?
合作探究1
已知:四边形ABCD中,AD∥BC,AD=BC,
试说明四边形ABCD是平行四边形.
B
C
A
D
A
D
B
C
A
B
C
D
线段BC可以看作由线段AD平移得到!
AB∥CD
平移后对应点所连的线段平行!
A
D
C
B
结论
∵AD∥BC且AD=BC
∴四边形ABCD是平行四边形.
(一组对边平行且相等的四边形是平行四边形).
一组对边平行且相等的四边形是平行四边形.
几何语言
例1:如图 ,在平行四边形ABCD中,E,F分别是
AD,BC的中点.
求证:四边形EBFD是平行四边形.
灵活运用:
变式:如图 ,在平行四边形ABCD中,E,F分别是
AD,BC上的一点,且AE=CF。
求证:四边形EBFD是平行四边形.
例1:如图 ,在平行四边形ABCD中,E,F分别是
AD,BC的中点.
求证:四边形EBFD是平行四边形.
灵活运用:
变式:如图 ,在平行四边形ABCD中,E,F分别是
AD,BC上的一点,且AE=CF。
求证:四边形EBFD是平行四边形.
在四边形ABCD中,AB=CD,AD=BC.
四边形ABCD是平行四边形吗?证明你的结论.
A
D
C
B
合作探究2
A
D
C
B
两组对边分别相等的四边形是平行四边形.
∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
结论
几何语言
(两组对边分别相等的四边形是平行四边形)
如图,□ABCD中,AF=CH,DE=BG,
求证: EG和HF互相平分.
灵活运用:
通过本节课的学习和探索,你有哪些收获
小结与思考
一组对边平行且相等
两组对边分别平行
两组对边分别相等
的四边形是平行四边形.
2、平行四边形的判别方法:
1、从平移、中心对称、说理等不同角度探索了平行四边形的判别方法.
判断
(1)一组对边平行且另一组对边相等的四边形是
平行四边形; ( )
(2)两组对角都相等的四边形是平行四边形 ( )
(3)一组对边平行且一组对角相等的四边形是平行
边形; ( )
(4)一组对边平行,一组邻角互补的四边形是平行
四边形; ( )
(5)两组邻角互补的四边形是平行四边形. ( )
×
√
√
×
×
检测反馈
1.如图,在□ABCD中,AE⊥BD,CF⊥BD,垂足分别是E、F,求证:四边形AECF是平行四边形.
整合提升
2.如图,在□ABCD中,点E、F分别在AD、BC上,且AE=CF,AE、BE相交于点G,CE、DF相交于点H.
求证:EF与GH互相平分。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
