2021—2022学年苏科版数学八年级下册9.3.1平行四边形 课件(共15张PPT)
文档属性
| 名称 | 2021—2022学年苏科版数学八年级下册9.3.1平行四边形 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 319.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
9.3.1 平行四边形(1)
学习目标:
1.理解平行四边形的定义;
2.掌握平行四边形的性质;
3.几何题型的解答;
思考:下面的图片中,有你熟悉的图形吗?
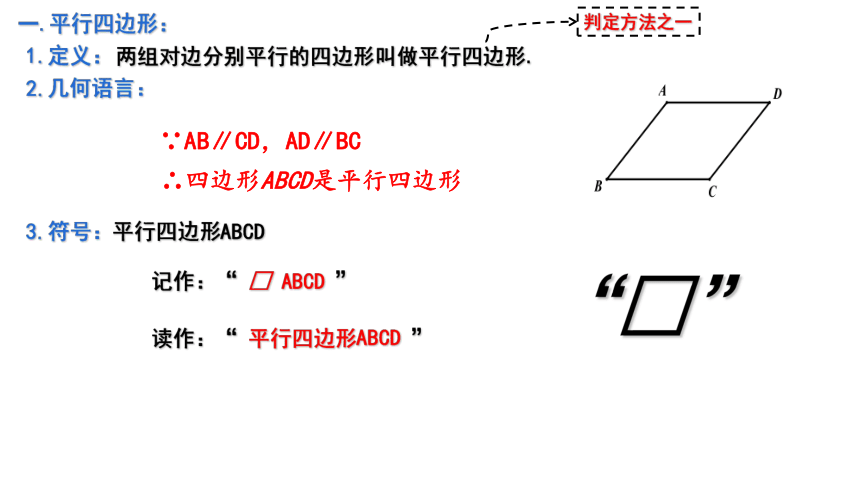
一.平行四边形:
1.定义:
两组对边分别平行的四边形叫做平行四边形.
2.几何语言:
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
判定方法之一
3.符号:平行四边形ABCD
记作:“ □ ABCD ”
读作:“ 平行四边形ABCD ”
“□”
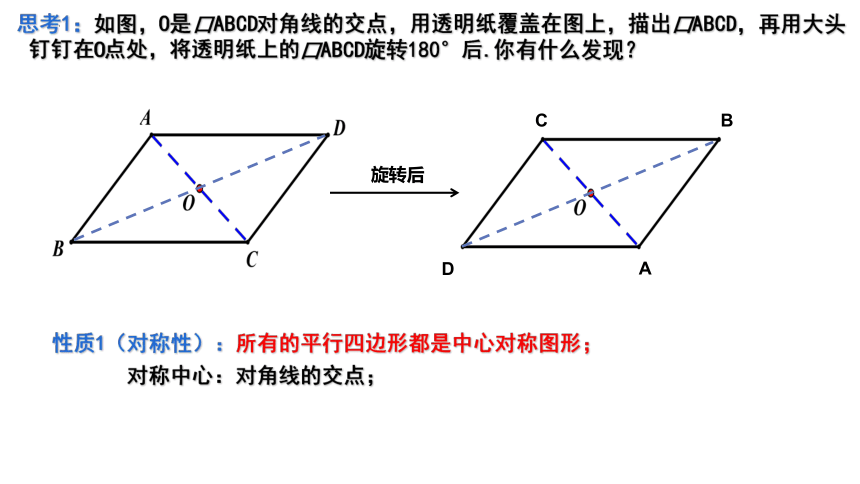
思考1:如图,O是口ABCD对角线的交点,用透明纸覆盖在图上,描出口ABCD,再用大头钉钉在O点处,将透明纸上的口ABCD旋转180°后.你有什么发现?
A
D
C
B
旋转后
性质1(对称性):所有的平行四边形都是中心对称图形;
对称中心:对角线的交点;
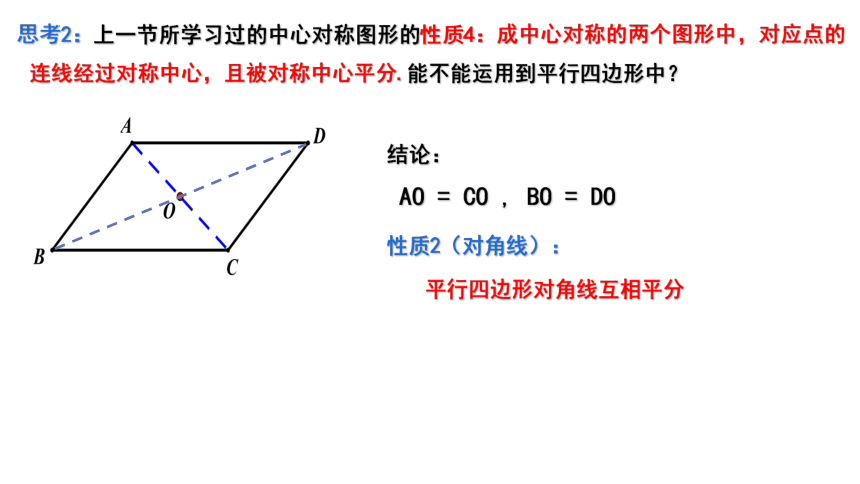
思考2:上一节所学习过的中心对称图形的性质4:成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.能不能运用到平行四边形中?
结论:
AO = CO , BO = DO
性质2(对角线):
平行四边形对角线互相平分
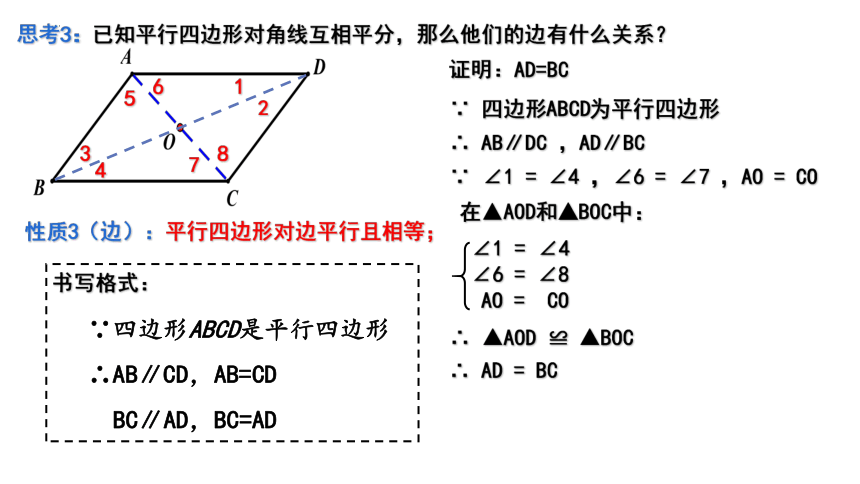
思考3:已知平行四边形对角线互相平分,那么他们的边有什么关系?
1
2
3
4
5
6
7
8
证明:AD=BC
∵ 四边形ABCD为平行四边形
∴ AB∥DC ,AD∥BC
∵ ∠1 = ∠4 ,∠6 = ∠7 ,AO = CO
在▲AOD和▲BOC中:
∠1 = ∠4
∠6 = ∠8
AO = CO
∴ ▲AOD ≌ ▲BOC
∴ AD = BC
性质3(边):平行四边形对边平行且相等;
书写格式:
∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD
BC∥AD,BC=AD
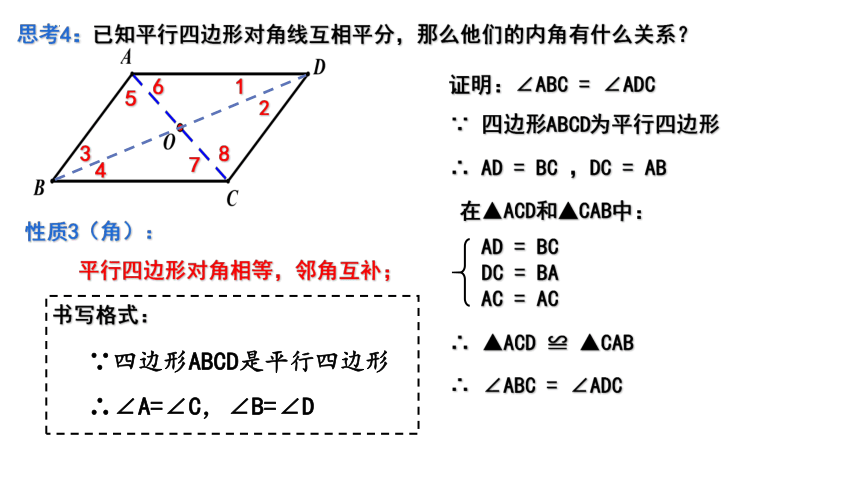
思考4:已知平行四边形对角线互相平分,那么他们的内角有什么关系?
1
2
3
4
5
6
7
8
证明:∠ABC = ∠ADC
∵ 四边形ABCD为平行四边形
∴ AD = BC ,DC = AB
在▲ACD和▲CAB中:
AD = BC
DC = BA
AC = AC
∴ ▲ACD ≌ ▲CAB
∴ ∠ABC = ∠ADC
性质3(角):
平行四边形对角相等,邻角互补;
书写格式:
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
例:如图,在平行四边形ABCD中,对角线AC、BD相交于
点O,且AB=25,BC=30,AC=28,BD=48.
(1)求AD、CD的长度;
(2)若∠ABC=60°,求∠ADC和∠BCD的度数;
(3)求△COD的周长.
变式训练:
(1)变式1:∠ABC+∠ADC =140°,则∠ABC=______,∠BAD=_______;
(2)变式2:∠ABC:∠BAD =1:3 ,则∠BCD=______, ∠ADC=_______;
(3)变式3: AC=28,BD=48,AB=m,则m的取值范围是_____________.
题型1:平行四边形+角平分线——一定产生等腰(边)三角形(突破口)
例:如图所示,在口ABCD中,BC=9,CD=5,若BE平分∠ABC,则ED=_______.
A
B
D
C
E
变式训练:若∠ABC的平分线BE将AD分成2cm和3cm的两部分,则平行四边形的周长为?
《课》 P42 - 1
题型2:平行四边形+翻折:
例:如图,口ABCD中,点E在AD上,以BE为折痕,将△ABE翻折,点A正好落在CD上的点F,△FDE的周长为8,△FCB的周长为22,求 FC的长.
《课》 P43 - 12
题型3:多个平行四边形中的传递性——等量代换
例:如图,点A、B、C分别在△DEF的各边上,且AB∥DE,BC∥EF,AC∥FD .
(1)求证:A、B、C分别是△DEF各边的中点.
(2)△ABC与△DEF的内角分别相等吗?为什么?
题型4:平行四边形的多解问题:
例1:学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里呢
D1
D2
A
B
C
D3
题型4:平行四边形的多解问题:
例2:在平面直角坐标系中, ABCD的顶点A、B、C的坐标分别是(0,1)、(-2,-2)、
(2,-2),则顶点D的坐标是______________________.
——坐标系中的多解问题
题型4:平行四边形的多解问题:
例3:在平面直角坐标系中,平行四边形的顶点A、B、C的坐标分别是(0,1)、(-2,-2)、
(2,-2),则顶点D的坐标是______________________.
——坐标系中的多解问题
(1)性质2(对角线):平行四边形对角线互相平分(且交与一点)
——对角线的交点就是中点
(2)中点坐标公式:A(x1 , y1)和B(x2 , y2)的中点为:
9.3.1 平行四边形(1)
学习目标:
1.理解平行四边形的定义;
2.掌握平行四边形的性质;
3.几何题型的解答;
思考:下面的图片中,有你熟悉的图形吗?
一.平行四边形:
1.定义:
两组对边分别平行的四边形叫做平行四边形.
2.几何语言:
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
判定方法之一
3.符号:平行四边形ABCD
记作:“ □ ABCD ”
读作:“ 平行四边形ABCD ”
“□”
思考1:如图,O是口ABCD对角线的交点,用透明纸覆盖在图上,描出口ABCD,再用大头钉钉在O点处,将透明纸上的口ABCD旋转180°后.你有什么发现?
A
D
C
B
旋转后
性质1(对称性):所有的平行四边形都是中心对称图形;
对称中心:对角线的交点;
思考2:上一节所学习过的中心对称图形的性质4:成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.能不能运用到平行四边形中?
结论:
AO = CO , BO = DO
性质2(对角线):
平行四边形对角线互相平分
思考3:已知平行四边形对角线互相平分,那么他们的边有什么关系?
1
2
3
4
5
6
7
8
证明:AD=BC
∵ 四边形ABCD为平行四边形
∴ AB∥DC ,AD∥BC
∵ ∠1 = ∠4 ,∠6 = ∠7 ,AO = CO
在▲AOD和▲BOC中:
∠1 = ∠4
∠6 = ∠8
AO = CO
∴ ▲AOD ≌ ▲BOC
∴ AD = BC
性质3(边):平行四边形对边平行且相等;
书写格式:
∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD
BC∥AD,BC=AD
思考4:已知平行四边形对角线互相平分,那么他们的内角有什么关系?
1
2
3
4
5
6
7
8
证明:∠ABC = ∠ADC
∵ 四边形ABCD为平行四边形
∴ AD = BC ,DC = AB
在▲ACD和▲CAB中:
AD = BC
DC = BA
AC = AC
∴ ▲ACD ≌ ▲CAB
∴ ∠ABC = ∠ADC
性质3(角):
平行四边形对角相等,邻角互补;
书写格式:
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
例:如图,在平行四边形ABCD中,对角线AC、BD相交于
点O,且AB=25,BC=30,AC=28,BD=48.
(1)求AD、CD的长度;
(2)若∠ABC=60°,求∠ADC和∠BCD的度数;
(3)求△COD的周长.
变式训练:
(1)变式1:∠ABC+∠ADC =140°,则∠ABC=______,∠BAD=_______;
(2)变式2:∠ABC:∠BAD =1:3 ,则∠BCD=______, ∠ADC=_______;
(3)变式3: AC=28,BD=48,AB=m,则m的取值范围是_____________.
题型1:平行四边形+角平分线——一定产生等腰(边)三角形(突破口)
例:如图所示,在口ABCD中,BC=9,CD=5,若BE平分∠ABC,则ED=_______.
A
B
D
C
E
变式训练:若∠ABC的平分线BE将AD分成2cm和3cm的两部分,则平行四边形的周长为?
《课》 P42 - 1
题型2:平行四边形+翻折:
例:如图,口ABCD中,点E在AD上,以BE为折痕,将△ABE翻折,点A正好落在CD上的点F,△FDE的周长为8,△FCB的周长为22,求 FC的长.
《课》 P43 - 12
题型3:多个平行四边形中的传递性——等量代换
例:如图,点A、B、C分别在△DEF的各边上,且AB∥DE,BC∥EF,AC∥FD .
(1)求证:A、B、C分别是△DEF各边的中点.
(2)△ABC与△DEF的内角分别相等吗?为什么?
题型4:平行四边形的多解问题:
例1:学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里呢
D1
D2
A
B
C
D3
题型4:平行四边形的多解问题:
例2:在平面直角坐标系中, ABCD的顶点A、B、C的坐标分别是(0,1)、(-2,-2)、
(2,-2),则顶点D的坐标是______________________.
——坐标系中的多解问题
题型4:平行四边形的多解问题:
例3:在平面直角坐标系中,平行四边形的顶点A、B、C的坐标分别是(0,1)、(-2,-2)、
(2,-2),则顶点D的坐标是______________________.
——坐标系中的多解问题
(1)性质2(对角线):平行四边形对角线互相平分(且交与一点)
——对角线的交点就是中点
(2)中点坐标公式:A(x1 , y1)和B(x2 , y2)的中点为:
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
