2021--2022学年苏科版八年级数学下册9.5三角形的中位线 课件(共25张PPT)
文档属性
| 名称 | 2021--2022学年苏科版八年级数学下册9.5三角形的中位线 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 498.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 19:49:38 | ||
图片预览





文档简介
(共25张PPT)
2022
9.5 三角形的中位线
八年级下册
学习目标
1.理解三角形中位线的概念。
2.会运用中位线定理计算证明。
3.能利用三角形中位线定理解决实际问题。
重点
理解三角形中位线的概念。
难点
能利用三角形中位线定理解决实际问题。
情景创设
1
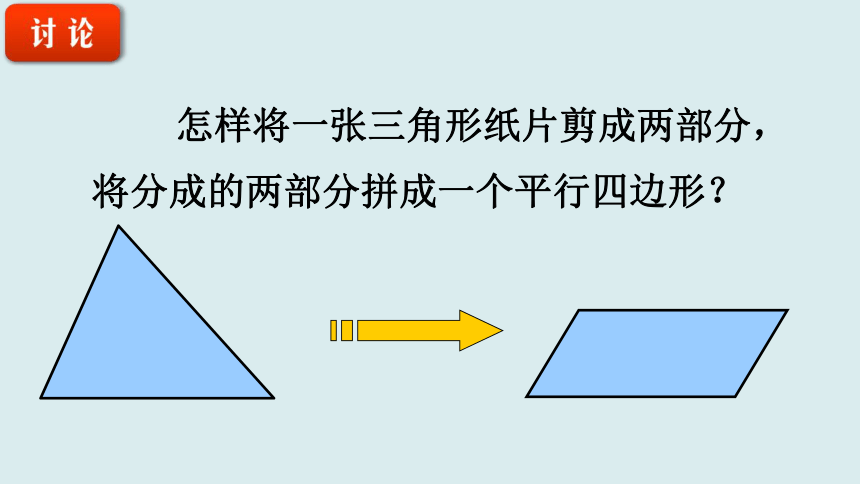
怎样将一张三角形纸片剪成两部分,将分成的两部分拼成一个平行四边形?
议题引领
2
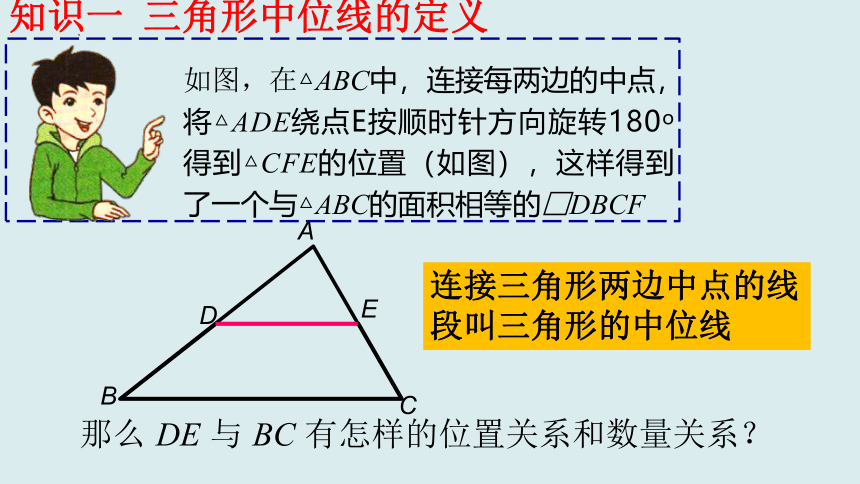
如图,在△ABC中,连接每两边的中点,将△ADE绕点E按顺时针方向旋转180o得到△CFE的位置(如图),这样得到了一个与△ABC的面积相等的□DBCF
A
B
C
D
E
A
D
E
F
你能解释这么做
的原因吗?
如图,在△ABC中,连接每两边的中点,将△ADE绕点E按顺时针方向旋转180o得到△CFE的位置(如图),这样得到了一个与△ABC的面积相等的□DBCF
那么 DE 与 BC 有怎样的位置关系和数量关系?
A
B
C
D
E
知识一 三角形中位线的定义
连接三角形两边中点的线段叫三角形的中位线
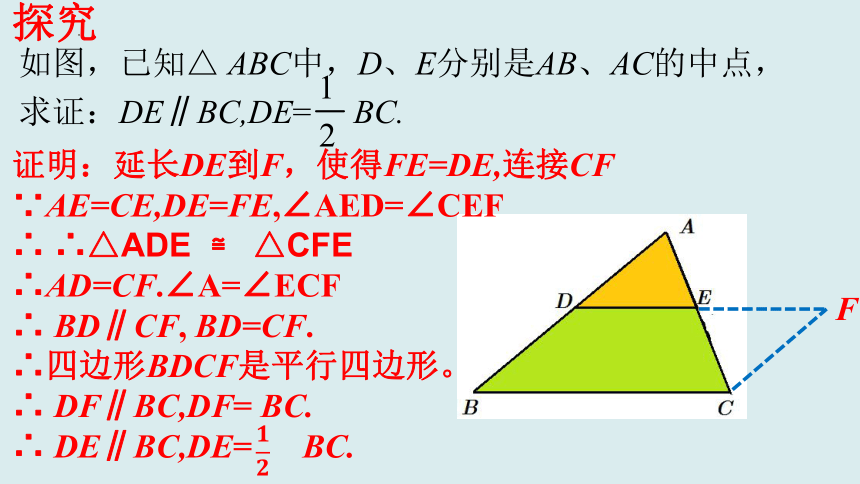
如图,已知△ ABC中,D、E分别是AB、AC的中点,求证:DE∥BC,DE= BC.
F
证明:延长DE到F,使得FE=DE,连接CF
∵AE=CE,DE=FE,∠AED=∠CEF
∴ ∴△ADE ≌ △CFE
∴AD=CF.∠A=∠ECF
∴ BD∥CF, BD=CF.
∴四边形BDCF是平行四边形。
∴ DF∥BC,DF= BC.
∴ DE∥BC,DE= BC.
探究
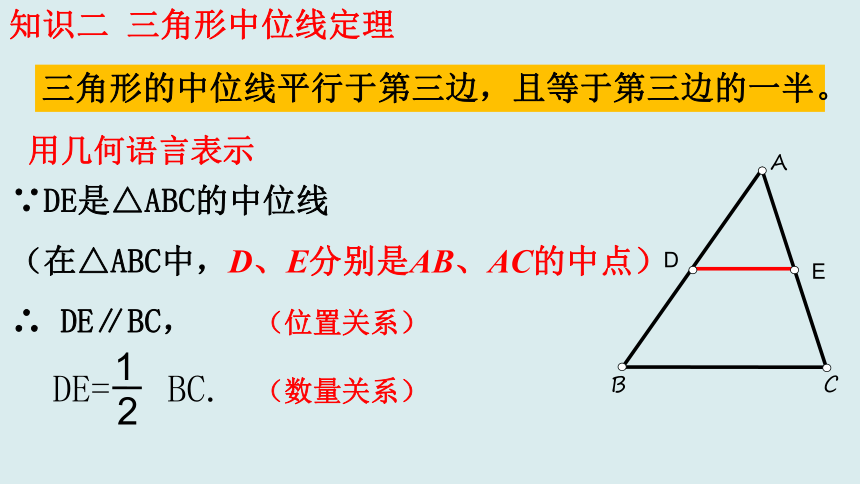
知识二 三角形中位线定理
三角形的中位线平行于第三边,且等于第三边的一半。
C
A
B
D
E
用几何语言表示
∵DE是△ABC的中位线
(在△ABC中,D、E分别是AB、AC的中点)
∴ DE∥BC,
DE= BC.
2
1
(数量关系)
(位置关系)
1.如图:在△ABC中,DE是中位线。
(1)若∠ADE=60°,则∠B= ;
(2)若BC=8cm,则DE= cm.
(3)DE +BC=12cm,则BC=
60°
4
8cm
6cm
2.若等腰△ABC的周长40cm,AB=AC=14cm,则中位线DE=
E
A
B
C
D
随堂练习
3.如图,在 ABCD中,AD=6,点E,F分别是BD,CD的中点,则EF等于( )
A.2 B.3 C.4 D.5
B
4.如图,在直角三角形ABC中,∠C=90°,AB=10,AC=8,点E,F分别为AC和AB的中点,则 EF=( )
A.3 B.4 C.5 D.6
A
随堂练习
5.如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,连接EF、EG、FG,则△EFG是什么三角形?为什么?
图1
解:△EFG是等腰三角形
∵E,F,G分别是AB,
CD,AC的中点.
∴GF= AD,GE= BC.
又∵AD=BC,
∴GF=GE,
即△EFG是等腰三角形
随堂练习
B
A
C
D
E
36
6.如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连结AC和 BC,分别取AC和BC的中点D、E.
①如果DE=36m,那么A、B两点间的距离是多少?为什么?
解:(1)∵ D、E是AC、BC的中点
∴ DE是△ABC的中位线
∴ DE= AB
∵ DE=36米
∴ AB=2DE=72米
随堂练习
B
A
C
D
E
36
②如果D、E两点之间还有阻隔,你有什么解决办法?
6.如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连结AC和 BC,分别取AC和BC的中点D、E.
解
(2)当DE间还有建筑物时,可以分别取CD、CE的中点F、G,
测得FG的长,就可以求得A、B两点间的距离.
随堂练习
合作学习
3
(1)相同点:都和边的中点有关;
(2)不同点:
三角形中位线的两个端点都是边的中点;
三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。
C
B
A
E
D
概念对比
C
B
A
D
中线DC
中位线DE
三角形的中位线与中线有什么相同点和不同点?
A
B
C
E
D
F
如图:三角形ABC中,点D、E、F分别是AB、BC、AC的中点.
(2)三角形的中线有______________
(1)三角形的中位线有____________
AE、BF、CD
DE、DF、EF
练一练
(2)顺次连接对角线互相垂直的任意四边形的各边中
点所得的四边形是_________;
(3)顺次连接对角线相等的任意四边形的各边中点
所得的四边形是_________;
(4)顺次连接对角线互相垂直且相等的四边形的各边
中点所得的四边形是_________.
(1)顺次连接任意四边形的各边中点所得的四边形是_________;
平行四边形
菱 形
矩 形
正方形
判断中点四边形的形状
原四边形两条对角线 连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否为特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
总结
例已知:如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是菱形.
证明:在△BAC中,
∵BE = EA,BF = FC,
∴ (三角形的中位线等于第三边的一半)
同理
∵AC = BD,
∴ EF = FG = GH = HE.
四边形EFGH是菱形(四边相等的四边形是菱形)
成果展示
4
成果展示:
1、定义:
连接三角形两边中点的线段叫做三角形的中位线.
2、三角形的中位线定理:
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
数量关系:
位置关系:
DE∥BC
DE= BC.
C
A
B
D
E
检测反馈
5
1.如图,在△ABC中,D,E分别是边AB,AC的中点.若BC=6,∠B=70°,则DE= ,∠ADE= °.
3
70
2.如图,在△ABC中,D,E,F分别是BC,AB,AC的中点.如果△ABC的周长为20,那么△DEF的周长为( )
A.5 B.10 C.15 D.20
B
检测反馈
3.在Rt△ABC中,D为斜边AB的中点,E是AC的中点,且AC=6,
CD=5,则线段ED的长是 .
4
4.如图,D,E,F分别是△ABC的边AB,BC,AC的中点,连接DF,EF.求证:四边形BDFE是平行四边形.
证明:∵D,F分别是AB,AC的中点,
∴DF是△ABC的中位线,
∴DF∥BC.同理,EF∥AB,
∴四边形BDFE是平行四边形.
检测反馈
2022
9.5 三角形的中位线
八年级下册
学习目标
1.理解三角形中位线的概念。
2.会运用中位线定理计算证明。
3.能利用三角形中位线定理解决实际问题。
重点
理解三角形中位线的概念。
难点
能利用三角形中位线定理解决实际问题。
情景创设
1
怎样将一张三角形纸片剪成两部分,将分成的两部分拼成一个平行四边形?
议题引领
2
如图,在△ABC中,连接每两边的中点,将△ADE绕点E按顺时针方向旋转180o得到△CFE的位置(如图),这样得到了一个与△ABC的面积相等的□DBCF
A
B
C
D
E
A
D
E
F
你能解释这么做
的原因吗?
如图,在△ABC中,连接每两边的中点,将△ADE绕点E按顺时针方向旋转180o得到△CFE的位置(如图),这样得到了一个与△ABC的面积相等的□DBCF
那么 DE 与 BC 有怎样的位置关系和数量关系?
A
B
C
D
E
知识一 三角形中位线的定义
连接三角形两边中点的线段叫三角形的中位线
如图,已知△ ABC中,D、E分别是AB、AC的中点,求证:DE∥BC,DE= BC.
F
证明:延长DE到F,使得FE=DE,连接CF
∵AE=CE,DE=FE,∠AED=∠CEF
∴ ∴△ADE ≌ △CFE
∴AD=CF.∠A=∠ECF
∴ BD∥CF, BD=CF.
∴四边形BDCF是平行四边形。
∴ DF∥BC,DF= BC.
∴ DE∥BC,DE= BC.
探究
知识二 三角形中位线定理
三角形的中位线平行于第三边,且等于第三边的一半。
C
A
B
D
E
用几何语言表示
∵DE是△ABC的中位线
(在△ABC中,D、E分别是AB、AC的中点)
∴ DE∥BC,
DE= BC.
2
1
(数量关系)
(位置关系)
1.如图:在△ABC中,DE是中位线。
(1)若∠ADE=60°,则∠B= ;
(2)若BC=8cm,则DE= cm.
(3)DE +BC=12cm,则BC=
60°
4
8cm
6cm
2.若等腰△ABC的周长40cm,AB=AC=14cm,则中位线DE=
E
A
B
C
D
随堂练习
3.如图,在 ABCD中,AD=6,点E,F分别是BD,CD的中点,则EF等于( )
A.2 B.3 C.4 D.5
B
4.如图,在直角三角形ABC中,∠C=90°,AB=10,AC=8,点E,F分别为AC和AB的中点,则 EF=( )
A.3 B.4 C.5 D.6
A
随堂练习
5.如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,连接EF、EG、FG,则△EFG是什么三角形?为什么?
图1
解:△EFG是等腰三角形
∵E,F,G分别是AB,
CD,AC的中点.
∴GF= AD,GE= BC.
又∵AD=BC,
∴GF=GE,
即△EFG是等腰三角形
随堂练习
B
A
C
D
E
36
6.如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连结AC和 BC,分别取AC和BC的中点D、E.
①如果DE=36m,那么A、B两点间的距离是多少?为什么?
解:(1)∵ D、E是AC、BC的中点
∴ DE是△ABC的中位线
∴ DE= AB
∵ DE=36米
∴ AB=2DE=72米
随堂练习
B
A
C
D
E
36
②如果D、E两点之间还有阻隔,你有什么解决办法?
6.如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连结AC和 BC,分别取AC和BC的中点D、E.
解
(2)当DE间还有建筑物时,可以分别取CD、CE的中点F、G,
测得FG的长,就可以求得A、B两点间的距离.
随堂练习
合作学习
3
(1)相同点:都和边的中点有关;
(2)不同点:
三角形中位线的两个端点都是边的中点;
三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。
C
B
A
E
D
概念对比
C
B
A
D
中线DC
中位线DE
三角形的中位线与中线有什么相同点和不同点?
A
B
C
E
D
F
如图:三角形ABC中,点D、E、F分别是AB、BC、AC的中点.
(2)三角形的中线有______________
(1)三角形的中位线有____________
AE、BF、CD
DE、DF、EF
练一练
(2)顺次连接对角线互相垂直的任意四边形的各边中
点所得的四边形是_________;
(3)顺次连接对角线相等的任意四边形的各边中点
所得的四边形是_________;
(4)顺次连接对角线互相垂直且相等的四边形的各边
中点所得的四边形是_________.
(1)顺次连接任意四边形的各边中点所得的四边形是_________;
平行四边形
菱 形
矩 形
正方形
判断中点四边形的形状
原四边形两条对角线 连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否为特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
总结
例已知:如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是菱形.
证明:在△BAC中,
∵BE = EA,BF = FC,
∴ (三角形的中位线等于第三边的一半)
同理
∵AC = BD,
∴ EF = FG = GH = HE.
四边形EFGH是菱形(四边相等的四边形是菱形)
成果展示
4
成果展示:
1、定义:
连接三角形两边中点的线段叫做三角形的中位线.
2、三角形的中位线定理:
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
数量关系:
位置关系:
DE∥BC
DE= BC.
C
A
B
D
E
检测反馈
5
1.如图,在△ABC中,D,E分别是边AB,AC的中点.若BC=6,∠B=70°,则DE= ,∠ADE= °.
3
70
2.如图,在△ABC中,D,E,F分别是BC,AB,AC的中点.如果△ABC的周长为20,那么△DEF的周长为( )
A.5 B.10 C.15 D.20
B
检测反馈
3.在Rt△ABC中,D为斜边AB的中点,E是AC的中点,且AC=6,
CD=5,则线段ED的长是 .
4
4.如图,D,E,F分别是△ABC的边AB,BC,AC的中点,连接DF,EF.求证:四边形BDFE是平行四边形.
证明:∵D,F分别是AB,AC的中点,
∴DF是△ABC的中位线,
∴DF∥BC.同理,EF∥AB,
∴四边形BDFE是平行四边形.
检测反馈
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
