苏科版八年级数学下册 9.5 三角形的中位线 教案(表格式)
文档属性
| 名称 | 苏科版八年级数学下册 9.5 三角形的中位线 教案(表格式) | 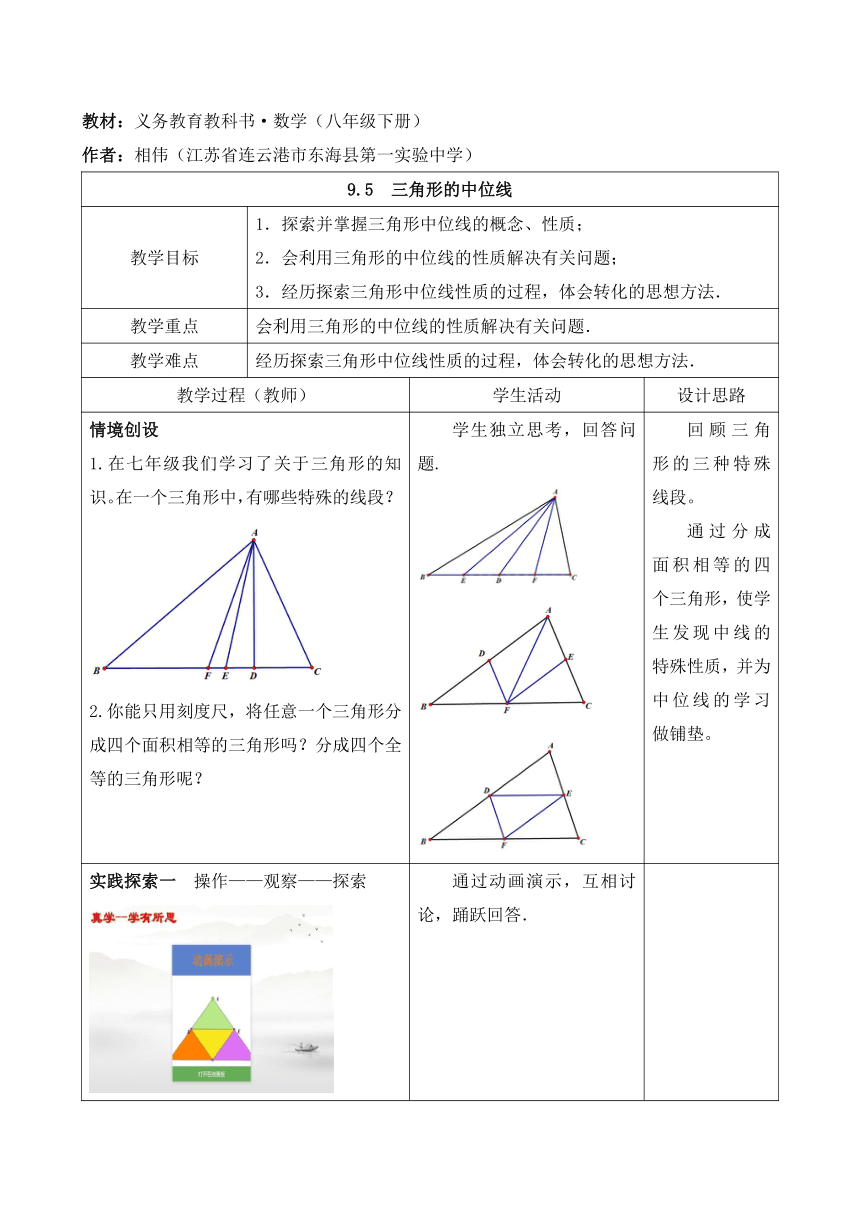 | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 19:43:00 | ||
图片预览


文档简介
教材:义务教育教科书·数学(八年级下册)
作者:相伟(江苏省连云港市东海县第一实验中学)
9.5 三角形的中位线
教学目标 1.探索并掌握三角形中位线的概念、性质; 2.会利用三角形的中位线的性质解决有关问题; 3.经历探索三角形中位线性质的过程,体会转化的思想方法.
教学重点 会利用三角形的中位线的性质解决有关问题.
教学难点 经历探索三角形中位线性质的过程,体会转化的思想方法.
教学过程(教师) 学生活动 设计思路
情境创设 1.在七年级我们学习了关于三角形的知识。在一个三角形中,有哪些特殊的线段? 2.你能只用刻度尺,将任意一个三角形分成四个面积相等的三角形吗?分成四个全等的三角形呢? 学生独立思考,回答问题. 回顾三角形的三种特殊线段。 通过分成面积相等的四个三角形,使学生发现中线的特殊性质,并为中位线的学习做铺垫。
实践探索一 操作——观察——探索 3.在刚才的动画演示中,DE、EF、DF三条线段的端点各是什么点? 4.引入三角形中位线的概念. 5.一个三角形有几条中位线? 6.中点三角形:顺次连接三角形各边中点所组成的三角形。 7.三角形的中位线和三角形的中线一样吗?有何异同点? 通过动画演示,互相讨论,踊跃回答. 通过问题串,引出三角形中位线定义,并发现其与中线的异同点。
实践探索二 探索三角形中位线的性质. 8.通过度量,你能发现三角形的一条中位线和它所对边的关系是什么吗? 三角形的中位线平行于第三边,并且等于第三边的一半. 9.通过推理,你能证明三角形中位线性质吗? 首先,在实践探索一的基础上,通过独立思考和合作交流,得出三角形中位线的性质;接着,观看微课,学习证明过程。 小组选取队员参加希沃白板5中的游戏化课堂活动。 三角形中位线的性质是三角形的一个重要性质,通过学生相互讨论,归纳这个性质的特点:在同一条件下,有2个结论,一个表示位置关系,另一个表示数量关系,提醒学生在应用该性质时,要根据需要,选用结论.
展示交流一 例.已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。 求证:四边形EFGH是平行四边形。 小组内讨论交流.小组推荐代表发言,其他小组可作补充. 教师引导,梳理思路, 最后在黑板上写出详细的过程. 能运用三角形中位线的性质进行推理. 教师的板书很重要,有着关键的示范作用,能培养学生有条理的说理能力.
展示交流二 变式1.已知:如左图,在矩形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是菱形。 变式2.已知:如右图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,AC=BD。求证:四边形EFGH是菱形。 变式3.已知:如左图,在菱形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是矩形。 变式4.已知:如右图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,AC⊥BD。求证:四边形EFGH是矩形。 根据题意,画出图形; 小组内讨论交流; 小组推荐代表阐述思路; 通过希沃白板5中的希沃授课助手,将两名学生详细证明过程投影到交互式电子屏上; 师生共同纠错; 教师及时评价(表扬激励为主),找出学生的闪光点. 在上一题的基础上,放手让学生自己完成过程,有助于知识的进一步强化. 在课堂上要充分调动学生的学习积极性,积极融入课堂,积极思考,踊跃发言,锻炼思维能力,这对学好数学非常有帮助.
问:通过例题和四个变式题,你有什么发现? 小组合作讨论; 教师到学生中间,聆听他们的想法,发现有不正确的及时指出,给予充足的时间,让学生动脑思考; 小组选取队员参加希沃白板5中的游戏化课堂活动,从而得出完整的答案。 引导学生体会由特殊到一般的思想,掌握中点四边形的形状判断。
小结: 1.三角形中位线定义 2.三角形中位线性质 3.中点三角形的定义及性质 4.中点四边形的形状判断 学生在小组内总结,强化知识巩固. 师生互动,锻炼学生的口头表达能力,培养学生勇于发表自己看法的能力.
课堂检测: 利用希沃白板5中的题库进行课堂检测。教师适时以小组为整体进行激励性评价,强调集体的力量,培养学生的团队合作意识,对学生今后的人生发展很有帮助. 通过课堂检测,利用小组竞答的形式,使学生掌握本节课所学知识,并激发学生学习数学的信心和荣誉感。
作者:相伟(江苏省连云港市东海县第一实验中学)
9.5 三角形的中位线
教学目标 1.探索并掌握三角形中位线的概念、性质; 2.会利用三角形的中位线的性质解决有关问题; 3.经历探索三角形中位线性质的过程,体会转化的思想方法.
教学重点 会利用三角形的中位线的性质解决有关问题.
教学难点 经历探索三角形中位线性质的过程,体会转化的思想方法.
教学过程(教师) 学生活动 设计思路
情境创设 1.在七年级我们学习了关于三角形的知识。在一个三角形中,有哪些特殊的线段? 2.你能只用刻度尺,将任意一个三角形分成四个面积相等的三角形吗?分成四个全等的三角形呢? 学生独立思考,回答问题. 回顾三角形的三种特殊线段。 通过分成面积相等的四个三角形,使学生发现中线的特殊性质,并为中位线的学习做铺垫。
实践探索一 操作——观察——探索 3.在刚才的动画演示中,DE、EF、DF三条线段的端点各是什么点? 4.引入三角形中位线的概念. 5.一个三角形有几条中位线? 6.中点三角形:顺次连接三角形各边中点所组成的三角形。 7.三角形的中位线和三角形的中线一样吗?有何异同点? 通过动画演示,互相讨论,踊跃回答. 通过问题串,引出三角形中位线定义,并发现其与中线的异同点。
实践探索二 探索三角形中位线的性质. 8.通过度量,你能发现三角形的一条中位线和它所对边的关系是什么吗? 三角形的中位线平行于第三边,并且等于第三边的一半. 9.通过推理,你能证明三角形中位线性质吗? 首先,在实践探索一的基础上,通过独立思考和合作交流,得出三角形中位线的性质;接着,观看微课,学习证明过程。 小组选取队员参加希沃白板5中的游戏化课堂活动。 三角形中位线的性质是三角形的一个重要性质,通过学生相互讨论,归纳这个性质的特点:在同一条件下,有2个结论,一个表示位置关系,另一个表示数量关系,提醒学生在应用该性质时,要根据需要,选用结论.
展示交流一 例.已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。 求证:四边形EFGH是平行四边形。 小组内讨论交流.小组推荐代表发言,其他小组可作补充. 教师引导,梳理思路, 最后在黑板上写出详细的过程. 能运用三角形中位线的性质进行推理. 教师的板书很重要,有着关键的示范作用,能培养学生有条理的说理能力.
展示交流二 变式1.已知:如左图,在矩形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是菱形。 变式2.已知:如右图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,AC=BD。求证:四边形EFGH是菱形。 变式3.已知:如左图,在菱形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是矩形。 变式4.已知:如右图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,AC⊥BD。求证:四边形EFGH是矩形。 根据题意,画出图形; 小组内讨论交流; 小组推荐代表阐述思路; 通过希沃白板5中的希沃授课助手,将两名学生详细证明过程投影到交互式电子屏上; 师生共同纠错; 教师及时评价(表扬激励为主),找出学生的闪光点. 在上一题的基础上,放手让学生自己完成过程,有助于知识的进一步强化. 在课堂上要充分调动学生的学习积极性,积极融入课堂,积极思考,踊跃发言,锻炼思维能力,这对学好数学非常有帮助.
问:通过例题和四个变式题,你有什么发现? 小组合作讨论; 教师到学生中间,聆听他们的想法,发现有不正确的及时指出,给予充足的时间,让学生动脑思考; 小组选取队员参加希沃白板5中的游戏化课堂活动,从而得出完整的答案。 引导学生体会由特殊到一般的思想,掌握中点四边形的形状判断。
小结: 1.三角形中位线定义 2.三角形中位线性质 3.中点三角形的定义及性质 4.中点四边形的形状判断 学生在小组内总结,强化知识巩固. 师生互动,锻炼学生的口头表达能力,培养学生勇于发表自己看法的能力.
课堂检测: 利用希沃白板5中的题库进行课堂检测。教师适时以小组为整体进行激励性评价,强调集体的力量,培养学生的团队合作意识,对学生今后的人生发展很有帮助. 通过课堂检测,利用小组竞答的形式,使学生掌握本节课所学知识,并激发学生学习数学的信心和荣誉感。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
