苏科版八年级数学下册 第9章 中心对称图形——平行四边形 复习 课件(共20张PPT)
文档属性
| 名称 | 苏科版八年级数学下册 第9章 中心对称图形——平行四边形 复习 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 369.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 07:35:54 | ||
图片预览




文档简介
(共20张PPT)
第9章 中心对称图形——平行四边形 复习课件
A'
B'
B
O
A
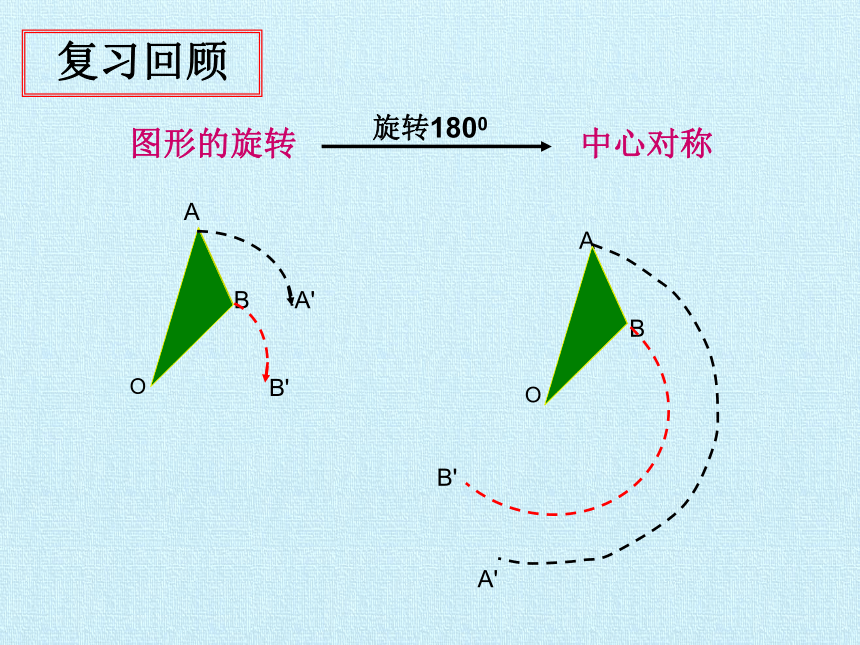
图形的旋转
中心对称
旋转1800
A'
B'
B
O
A
复习回顾
A
B
C
O
D
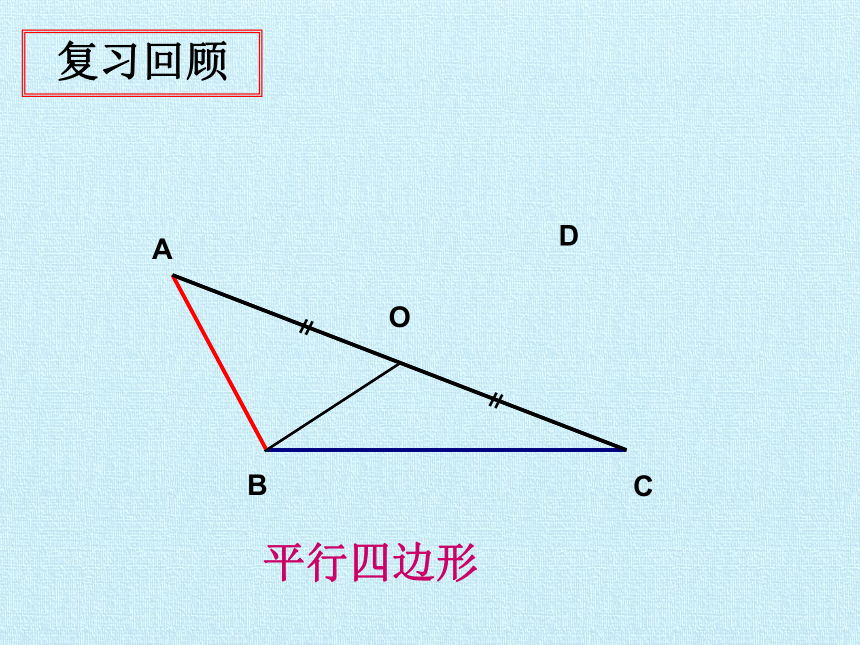
平行四边形
复习回顾
A
B
C
O
D
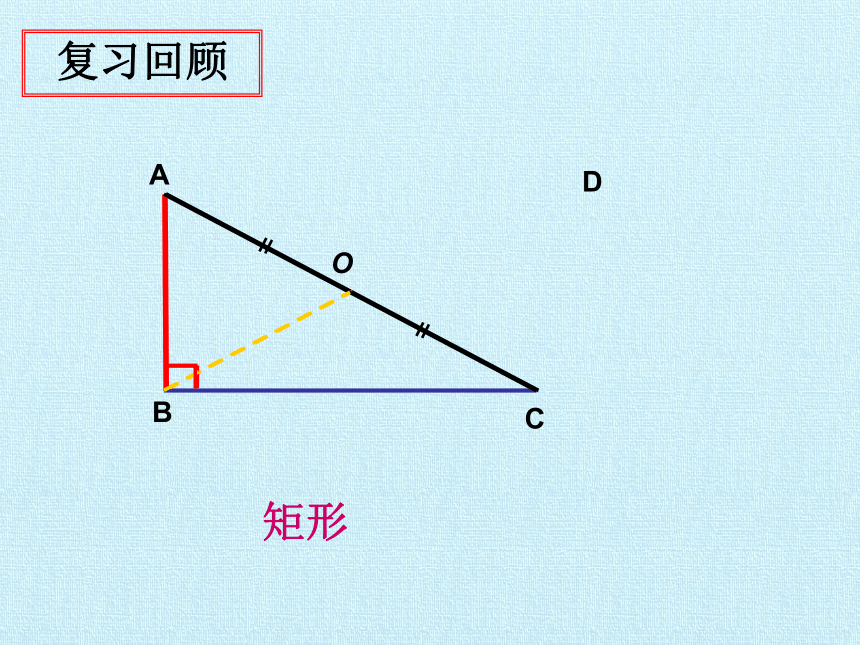
矩形
复习回顾
A
B
C
D
O
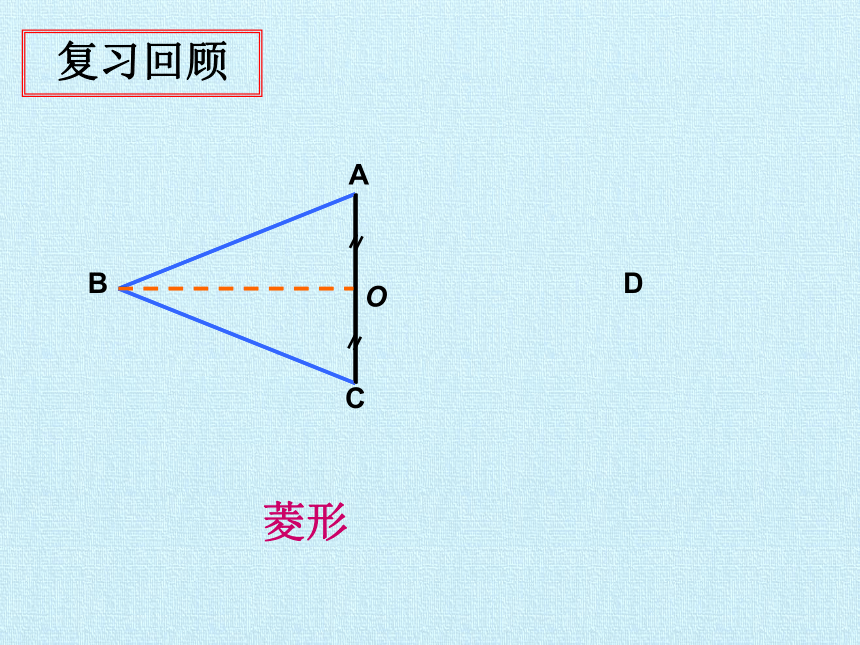
菱形
复习回顾
A
B
C
O
D
正方形
复习回顾
①平行四边形的对边平行;
②平行四边形的对边相等;
③平行四边形的对角相等;
④平行四边形的对角线互相平分。
①2组对边分别平行的四边形是平行四边形;
②2组对边分别相等的四边形是平行四边形;
③一组对边平行且相等的四边形是平行四边形;
④对角线互相平分的四边形是平行四边形。
性质
判定方法
性质
①矩形是特殊的平行四边形,它具有平行四边形的一切性质;
②矩形的四个角都是直角;
③矩形的对角线相等。
判定方法
①有一个角是直角的平行四边形是矩形;
②有3个角是直角的四边形是矩形;
③对角线相等的平行四边形是矩形。
①菱形是特殊的平行四边形,它具有平行四边形的一切性质;
②菱形的四条边相等;
③菱形的对角线互相垂直,并且每一条对角线平分一组对角。
性质
判定方法
①有一组邻边相等的平行四边形是菱形;
②四边都相等的四边形是菱形;
③对角线互相垂直的平行四边形是菱形。
性质
判定方法
正方形具有矩形的性质,同时又具有菱形的性质。
①有一组邻边相等并且有一个角是直角的平行
四边形是正方形;
②有一组邻边相等的矩形是正方形;
③有一个角是直角的菱形是正方形。
平行四边形、矩形、菱形、正方形之间的关系
1.矩形的两条对角线的夹角为600,较短的边长为12cm,则对角线长为 cm。
2.菱形的周长为20,一条对角线长为6,则另一条对角线长为 ,菱形的面积为_____。
3.如图,□ABCD的对角线AC、BD相交于点O,过点O的直线OM⊥AC;已知ΔCDM的周长是22㎝;则□ABCD的周长是 ㎝。
4.如图,正方形ABCD绕点A旋转后得到正方AB′C′D′
① 旋转角是 度。
② 若AB=1,则C′ D=_____。
基础练习
24
45
44
24
8
例1:如图,平行四边形 ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F,试说明四边形AFCE是菱形。
解:
在□ABCD中,AD//BC
∴∠EAO=∠OCF,∠AEO=∠OFC
∵AO=CO
∴ΔAOE≌ΔCOF
∴OE=OF
∴四边形AFCE是平行四边形
∵EF⊥AC
∴四边形AFCE是菱形
例题分析
例2:如图,在梯形ABCD中,AD//BC,AB//DE,AF//DC,E,F两点在边BC上,且四边形AEFD是平行四边形。
(1)AD与BC有何等量关系?请说明理由;
(2)当AB=DC时,试说明□AEFD是矩形。
A
D
C
F
E
B
解:
理由如下:
∴四边形ABED和四边形AFCD都是平行四边形。
∵AD//BC,AB//DE,AF//DC。
∴AD=BE,AD=CF
∵四边形AEFD是平行四边形
∴AD=EF
∴AD=BE=EF=FC
∴BC=3AD
(1)BC=3AD
(2)∵四边形ABED和四边形AFCD都是平行四边形
∴AB=DE,AF=DC
∴DE=AF
∵AB=DC
又∵四边形AEFD是平行四边形
∴四边形AEFD是矩形
例3:如图,矩形ABCD中,AE平分∠BAD,交BC于E,对角线AC、BD交于O,若∠OAE=15°。(1)试说明:OB=BE;(2)求∠BOE的度数
O
D
C
B
A
E
解:
(1)在矩形ABCD中,AE平分∠BAD
∴∠BAE=45°
∴∠BAO=60°
∵∠OAE=15°
∵矩形ABCD中,OA=OB
∴△OAB是等边三角形
∴AB=OB
∴AB=BE
∴OB=BE
(2)∵△OAB是等边三角形
∴∠ABO=60°
∴∠OBC=30°
∴∠BOE=75°
∵ OB=BE
例4:如图,正方形ABCD,AC、BD相交于点O,点E在AC上,连接BE,作AG⊥BE,垂足为G,且交直线BD于F。
(1)试说明:OE=OF;
(2)若点E在AC的延长线上,其余条件不变,(1)的结论还成立吗?画出图形,并说明理由。
E
F
O
G
D
C
B
A
解:
(1)在正方形ABCD中,AO=BO,∠AOF=∠BOE=90°
∵ AG⊥BE
∴∠AGB=90°
∵∠AFO=∠BFG
∴∠OAF=∠OBE
∴△AOF≌△BOE
∴OE=OF
A
B
C
D
O
E
F
G
(2)在正方形ABCD中,AO=BO,∠AOF=∠BOE=90 °
∵AG⊥BE
∴∠FGB=90°
∵∠OBE=∠GBF
∴∠AFO=∠BEO
∴△AOF≌△BOE
∴OE=OF
例4:如图,正方形ABCD,AC、BD相交于点O,点E在AC上,连接BE,作AG⊥BE,垂足为G,且交直线BD于F。
(1)试说明:OE=OF;
(2)若点E在AC的延长线上,其余条件不变,(1)的结论还成立吗?画出图形,并说明理由。
解:
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
A.1 B.2 C.3 D.不能确定
E
A
D
C
B
F
G
A
通过本堂课的学习,
说说你的收获和体会
谢 谢
第9章 中心对称图形——平行四边形 复习课件
A'
B'
B
O
A
图形的旋转
中心对称
旋转1800
A'
B'
B
O
A
复习回顾
A
B
C
O
D
平行四边形
复习回顾
A
B
C
O
D
矩形
复习回顾
A
B
C
D
O
菱形
复习回顾
A
B
C
O
D
正方形
复习回顾
①平行四边形的对边平行;
②平行四边形的对边相等;
③平行四边形的对角相等;
④平行四边形的对角线互相平分。
①2组对边分别平行的四边形是平行四边形;
②2组对边分别相等的四边形是平行四边形;
③一组对边平行且相等的四边形是平行四边形;
④对角线互相平分的四边形是平行四边形。
性质
判定方法
性质
①矩形是特殊的平行四边形,它具有平行四边形的一切性质;
②矩形的四个角都是直角;
③矩形的对角线相等。
判定方法
①有一个角是直角的平行四边形是矩形;
②有3个角是直角的四边形是矩形;
③对角线相等的平行四边形是矩形。
①菱形是特殊的平行四边形,它具有平行四边形的一切性质;
②菱形的四条边相等;
③菱形的对角线互相垂直,并且每一条对角线平分一组对角。
性质
判定方法
①有一组邻边相等的平行四边形是菱形;
②四边都相等的四边形是菱形;
③对角线互相垂直的平行四边形是菱形。
性质
判定方法
正方形具有矩形的性质,同时又具有菱形的性质。
①有一组邻边相等并且有一个角是直角的平行
四边形是正方形;
②有一组邻边相等的矩形是正方形;
③有一个角是直角的菱形是正方形。
平行四边形、矩形、菱形、正方形之间的关系
1.矩形的两条对角线的夹角为600,较短的边长为12cm,则对角线长为 cm。
2.菱形的周长为20,一条对角线长为6,则另一条对角线长为 ,菱形的面积为_____。
3.如图,□ABCD的对角线AC、BD相交于点O,过点O的直线OM⊥AC;已知ΔCDM的周长是22㎝;则□ABCD的周长是 ㎝。
4.如图,正方形ABCD绕点A旋转后得到正方AB′C′D′
① 旋转角是 度。
② 若AB=1,则C′ D=_____。
基础练习
24
45
44
24
8
例1:如图,平行四边形 ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F,试说明四边形AFCE是菱形。
解:
在□ABCD中,AD//BC
∴∠EAO=∠OCF,∠AEO=∠OFC
∵AO=CO
∴ΔAOE≌ΔCOF
∴OE=OF
∴四边形AFCE是平行四边形
∵EF⊥AC
∴四边形AFCE是菱形
例题分析
例2:如图,在梯形ABCD中,AD//BC,AB//DE,AF//DC,E,F两点在边BC上,且四边形AEFD是平行四边形。
(1)AD与BC有何等量关系?请说明理由;
(2)当AB=DC时,试说明□AEFD是矩形。
A
D
C
F
E
B
解:
理由如下:
∴四边形ABED和四边形AFCD都是平行四边形。
∵AD//BC,AB//DE,AF//DC。
∴AD=BE,AD=CF
∵四边形AEFD是平行四边形
∴AD=EF
∴AD=BE=EF=FC
∴BC=3AD
(1)BC=3AD
(2)∵四边形ABED和四边形AFCD都是平行四边形
∴AB=DE,AF=DC
∴DE=AF
∵AB=DC
又∵四边形AEFD是平行四边形
∴四边形AEFD是矩形
例3:如图,矩形ABCD中,AE平分∠BAD,交BC于E,对角线AC、BD交于O,若∠OAE=15°。(1)试说明:OB=BE;(2)求∠BOE的度数
O
D
C
B
A
E
解:
(1)在矩形ABCD中,AE平分∠BAD
∴∠BAE=45°
∴∠BAO=60°
∵∠OAE=15°
∵矩形ABCD中,OA=OB
∴△OAB是等边三角形
∴AB=OB
∴AB=BE
∴OB=BE
(2)∵△OAB是等边三角形
∴∠ABO=60°
∴∠OBC=30°
∴∠BOE=75°
∵ OB=BE
例4:如图,正方形ABCD,AC、BD相交于点O,点E在AC上,连接BE,作AG⊥BE,垂足为G,且交直线BD于F。
(1)试说明:OE=OF;
(2)若点E在AC的延长线上,其余条件不变,(1)的结论还成立吗?画出图形,并说明理由。
E
F
O
G
D
C
B
A
解:
(1)在正方形ABCD中,AO=BO,∠AOF=∠BOE=90°
∵ AG⊥BE
∴∠AGB=90°
∵∠AFO=∠BFG
∴∠OAF=∠OBE
∴△AOF≌△BOE
∴OE=OF
A
B
C
D
O
E
F
G
(2)在正方形ABCD中,AO=BO,∠AOF=∠BOE=90 °
∵AG⊥BE
∴∠FGB=90°
∵∠OBE=∠GBF
∴∠AFO=∠BEO
∴△AOF≌△BOE
∴OE=OF
例4:如图,正方形ABCD,AC、BD相交于点O,点E在AC上,连接BE,作AG⊥BE,垂足为G,且交直线BD于F。
(1)试说明:OE=OF;
(2)若点E在AC的延长线上,其余条件不变,(1)的结论还成立吗?画出图形,并说明理由。
解:
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
A.1 B.2 C.3 D.不能确定
E
A
D
C
B
F
G
A
通过本堂课的学习,
说说你的收获和体会
谢 谢
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
