青岛版八年级数学上册4.4数据的离散程度 课件(共13张PPT)
文档属性
| 名称 | 青岛版八年级数学上册4.4数据的离散程度 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
温故知新
1.平均数
2.众数
3.中位数
在一组数据中,出现次数最多的数据叫做这组数据的众数.
把一组数据从小到大排列,最中间的一个数(或最中间两个数的平均数)叫这组数据的中位数.
(
)
n
x
x
x
x
n
x
+
+
+
+
=
L
3
2
1
1
某农场分别在8块管理条件和自然条件相同、面积相等的实验田中,对加以两种小麦新品种进行对比试验,产量如下(单位:千克):
甲种小麦:804 984 989 817 919 840 912 1001 乙种小麦:856 932 930 855 872 901 897 918
哪个品种的小麦产量比较稳定?
序数
成绩/秒
甲的成绩统计图
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
成绩 /秒
乙的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
序数 1 2 3 4 5 6 7 8
甲的成绩/秒 12.0 12.2 13.0 12.6 13.1 12.5 12.4 12.2
乙的成绩/秒 12.2 12.4 12.7 12.5 12.9 12.2 12.8 12.3
交流与发现
时代中学田径队的甲乙两名运动员在8次百米跑训练中,成绩如下表:
你能用折线统计图表示上述数据吗?
成绩/秒
甲的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
成绩 /秒
乙的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
(1)在这8次训练中,甲、乙两名运动员的百米跑成绩的平均数、众数、中位数分别是多少?
(2)小亮说:“甲、乙两名运动员的百米跑成绩的平均数、众数中位数对应相同,因此他们的成绩一样”,你认为这种说法合适吗?
甲、乙两名运动员百米跑的平均成绩都是12.5秒,成绩的众数都是12.45秒、成绩的中位数都是12.2秒.
不合适.
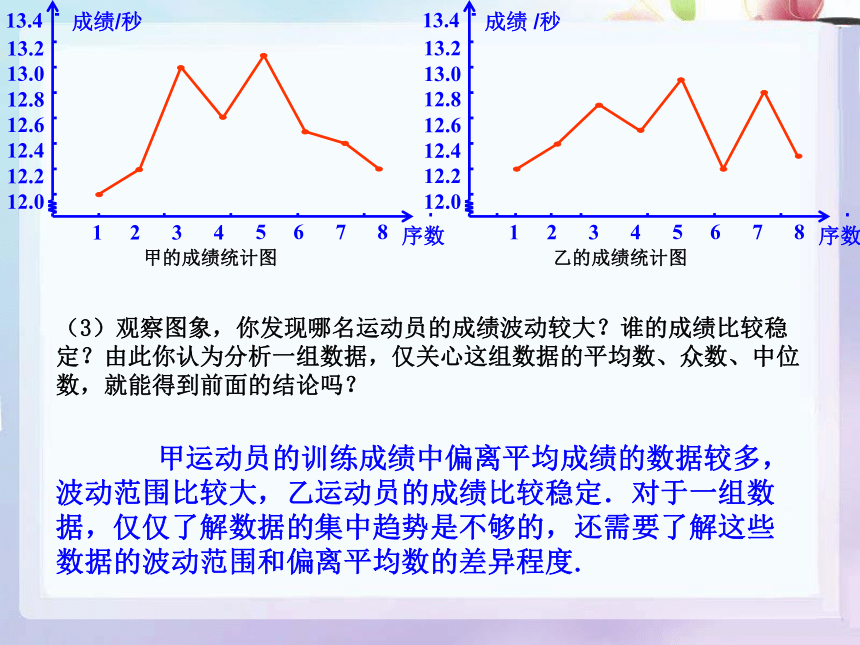
(3)观察图象,你发现哪名运动员的成绩波动较大?谁的成绩比较稳定?由此你认为分析一组数据,仅关心这组数据的平均数、众数、中位数,就能得到前面的结论吗?
成绩/秒
甲的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
成绩 /秒
乙的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
甲运动员的训练成绩中偏离平均成绩的数据较多,波动范围比较大,乙运动员的成绩比较稳定.对于一组数据,仅仅了解数据的集中趋势是不够的,还需要了解这些数据的波动范围和偏离平均数的差异程度.
我们通常用数据的离散程度来描述一组数据的波动范围和偏离平均数的差异程度。
数据的离散程度越大,表示数据分布的范围越广,越不稳定,平均数的代表性也就越小;
在实际生活和生产中,我们除了关心数据的集中趋势(平均数、中位数、众数)外,还要关注数据的离散程度,即一组数据的波动范围。
数据的离散程度越小,表示数据分布的越集中,变动范围越小,平均数的代表性就越大。
你能举出类似的例子吗?
两名同学在本学期数学成绩变化情况,两块
实验田里小麦高度情况等。
1.某砖厂从生产的甲、乙两种水泥砖中,各随机抽取了10 块,分别测出了它们的抗断强度.数据如下(单位:千克/平方厘米): 甲种砖:32.50 29.66 31.64 30.00 31.77 31.01 30.76 31.24 31.87 31.05 乙种砖:31.00 29.56 32.02 33.00 29.32 30.37 29.98 31.35 32.86 32.04 (1)甲种砖的平均抗断强度是多少? (2)乙种砖的平均抗断强度是多少? (3)作出统计图,你发现哪种砖的抗断强度波动较大?
311.5
311.5
乙种砖的抗断强度波动较大
练习
1.对于一组数据,仅仅了解数据的集中趋势是不够的,还需要了解这些数据的波动范围和偏离平均数的差异程度。
2.我们通常用数据的离散程度来描述一组数据的波动范围和偏离平均数的差异程度。
数据的离散程度越大,表示数据分布的范围越广,越不稳定,平均数的代表性也就越小;
数据的离散程度越小,表示数据分布的越集中,变动范围越小,平均数的代表性就越大。
在上面所提出的甲、乙两名运动员百米跑训练成绩的问题中, (l)甲运动员的最好成绩是多少? 最差成绩是多少? (2)乙运动员的最好成绩是多少? 最差成绩是多少?
拓展了解
成绩/秒
甲的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
成绩/秒
乙的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
因此,乙运动员的成绩比较稳定.
(3)你能根据问题(l)和(2)说明哪名运动员的成绩比较稳定吗?
一组数据中的最大数据与最小数据的差称为极差即
极差=最大数据一最小数据.
甲运动员百米跑的成绩的极差为:13.1-12.0 = 1.l (秒);
乙运动员百米跑的成绩的极差为:12.9-12.2 = 0.7 (秒),
12.0秒.
13.1秒.
12.2秒.
12.9秒.
号称“天下第一泉”的济南趵突泉,2003年9月6日在停喷548天后再次复涌.下表是小莹从因特网上收集的趵突泉复涌前后部分日最高地下水位的资料:
日期 06-11 06-20 07-05 07-13 08-23 09-05 09-06 09-21 10-06 10-22 11-14 12-05
日最高地下水位/米 22.99 21.99 21.61 22.76 25.33 26.84 27.01 27.50 28.01 28.99 28.49 28.64
在这组数据中,趵突泉日最高地下水位的极差是多少?
趵突泉日最高地下水位的级差=28.99-21.61=7.38(米)
练习
1.一组数据中的最大数据与最小数据的差称为极差,即
极差=最大数据一最小数据.
2.极差反映一组数据的波动范围,用极差描述这组数据的离散程度简单明了.极差越大,数据的离散程度越大。
3.由于极差忽视了一组数据中所有数据之间的差异,仅仅由其中的最大值和最小值所确定,个别远离群体的极端值在很大程度上会影响极差,因而极差往往不能充分反映一组数据的实际离散程度。
作业
习题4.4 复习与巩固 第1、2、3题
温故知新
1.平均数
2.众数
3.中位数
在一组数据中,出现次数最多的数据叫做这组数据的众数.
把一组数据从小到大排列,最中间的一个数(或最中间两个数的平均数)叫这组数据的中位数.
(
)
n
x
x
x
x
n
x
+
+
+
+
=
L
3
2
1
1
某农场分别在8块管理条件和自然条件相同、面积相等的实验田中,对加以两种小麦新品种进行对比试验,产量如下(单位:千克):
甲种小麦:804 984 989 817 919 840 912 1001 乙种小麦:856 932 930 855 872 901 897 918
哪个品种的小麦产量比较稳定?
序数
成绩/秒
甲的成绩统计图
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
成绩 /秒
乙的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
序数 1 2 3 4 5 6 7 8
甲的成绩/秒 12.0 12.2 13.0 12.6 13.1 12.5 12.4 12.2
乙的成绩/秒 12.2 12.4 12.7 12.5 12.9 12.2 12.8 12.3
交流与发现
时代中学田径队的甲乙两名运动员在8次百米跑训练中,成绩如下表:
你能用折线统计图表示上述数据吗?
成绩/秒
甲的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
成绩 /秒
乙的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
(1)在这8次训练中,甲、乙两名运动员的百米跑成绩的平均数、众数、中位数分别是多少?
(2)小亮说:“甲、乙两名运动员的百米跑成绩的平均数、众数中位数对应相同,因此他们的成绩一样”,你认为这种说法合适吗?
甲、乙两名运动员百米跑的平均成绩都是12.5秒,成绩的众数都是12.45秒、成绩的中位数都是12.2秒.
不合适.
(3)观察图象,你发现哪名运动员的成绩波动较大?谁的成绩比较稳定?由此你认为分析一组数据,仅关心这组数据的平均数、众数、中位数,就能得到前面的结论吗?
成绩/秒
甲的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
成绩 /秒
乙的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
甲运动员的训练成绩中偏离平均成绩的数据较多,波动范围比较大,乙运动员的成绩比较稳定.对于一组数据,仅仅了解数据的集中趋势是不够的,还需要了解这些数据的波动范围和偏离平均数的差异程度.
我们通常用数据的离散程度来描述一组数据的波动范围和偏离平均数的差异程度。
数据的离散程度越大,表示数据分布的范围越广,越不稳定,平均数的代表性也就越小;
在实际生活和生产中,我们除了关心数据的集中趋势(平均数、中位数、众数)外,还要关注数据的离散程度,即一组数据的波动范围。
数据的离散程度越小,表示数据分布的越集中,变动范围越小,平均数的代表性就越大。
你能举出类似的例子吗?
两名同学在本学期数学成绩变化情况,两块
实验田里小麦高度情况等。
1.某砖厂从生产的甲、乙两种水泥砖中,各随机抽取了10 块,分别测出了它们的抗断强度.数据如下(单位:千克/平方厘米): 甲种砖:32.50 29.66 31.64 30.00 31.77 31.01 30.76 31.24 31.87 31.05 乙种砖:31.00 29.56 32.02 33.00 29.32 30.37 29.98 31.35 32.86 32.04 (1)甲种砖的平均抗断强度是多少? (2)乙种砖的平均抗断强度是多少? (3)作出统计图,你发现哪种砖的抗断强度波动较大?
311.5
311.5
乙种砖的抗断强度波动较大
练习
1.对于一组数据,仅仅了解数据的集中趋势是不够的,还需要了解这些数据的波动范围和偏离平均数的差异程度。
2.我们通常用数据的离散程度来描述一组数据的波动范围和偏离平均数的差异程度。
数据的离散程度越大,表示数据分布的范围越广,越不稳定,平均数的代表性也就越小;
数据的离散程度越小,表示数据分布的越集中,变动范围越小,平均数的代表性就越大。
在上面所提出的甲、乙两名运动员百米跑训练成绩的问题中, (l)甲运动员的最好成绩是多少? 最差成绩是多少? (2)乙运动员的最好成绩是多少? 最差成绩是多少?
拓展了解
成绩/秒
甲的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
成绩/秒
乙的成绩统计图
序数
1
2
3
4
5
6
7
8
12.2
12.0
12.4
12.6
12.8
13.0
13.2
13.4
因此,乙运动员的成绩比较稳定.
(3)你能根据问题(l)和(2)说明哪名运动员的成绩比较稳定吗?
一组数据中的最大数据与最小数据的差称为极差即
极差=最大数据一最小数据.
甲运动员百米跑的成绩的极差为:13.1-12.0 = 1.l (秒);
乙运动员百米跑的成绩的极差为:12.9-12.2 = 0.7 (秒),
12.0秒.
13.1秒.
12.2秒.
12.9秒.
号称“天下第一泉”的济南趵突泉,2003年9月6日在停喷548天后再次复涌.下表是小莹从因特网上收集的趵突泉复涌前后部分日最高地下水位的资料:
日期 06-11 06-20 07-05 07-13 08-23 09-05 09-06 09-21 10-06 10-22 11-14 12-05
日最高地下水位/米 22.99 21.99 21.61 22.76 25.33 26.84 27.01 27.50 28.01 28.99 28.49 28.64
在这组数据中,趵突泉日最高地下水位的极差是多少?
趵突泉日最高地下水位的级差=28.99-21.61=7.38(米)
练习
1.一组数据中的最大数据与最小数据的差称为极差,即
极差=最大数据一最小数据.
2.极差反映一组数据的波动范围,用极差描述这组数据的离散程度简单明了.极差越大,数据的离散程度越大。
3.由于极差忽视了一组数据中所有数据之间的差异,仅仅由其中的最大值和最小值所确定,个别远离群体的极端值在很大程度上会影响极差,因而极差往往不能充分反映一组数据的实际离散程度。
作业
习题4.4 复习与巩固 第1、2、3题
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
