3.2.2 圆的对称性
图片预览



文档简介
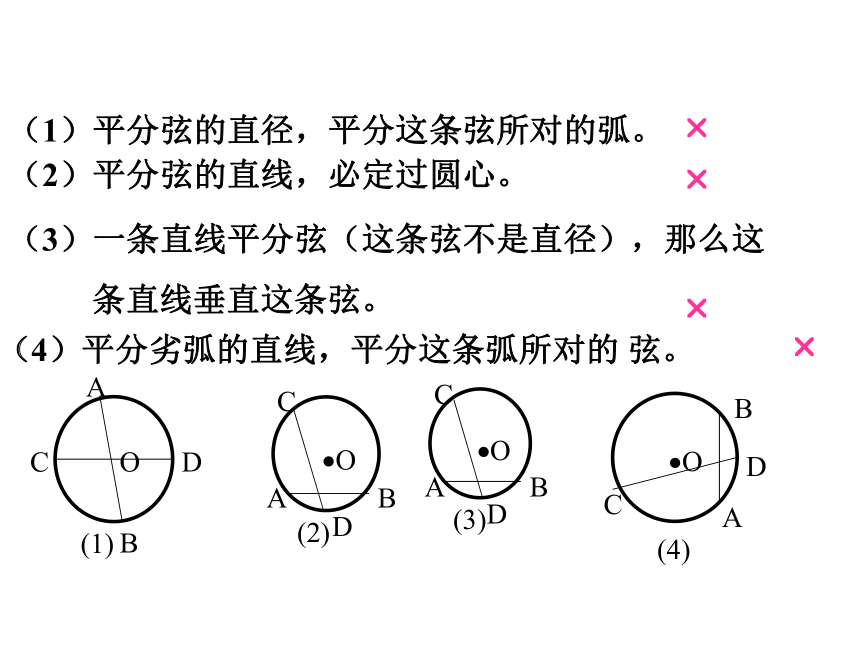
课件28张PPT。(1)平分弦的直径,平分这条弦所对的弧。(2)平分弦的直线,必定过圆心。(3)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。???(4)平分劣弧的直线,平分这条弧所对的 弦。?变式训练:1.下列说法中,不成立的是 ( )
A.弦的垂直平分线必过圆心。
B.弦(不是直径)的中点与圆心的连线垂直平分这条弦。
C.垂直于弦的直线经过圆心,且平分这条弦所对的弧。
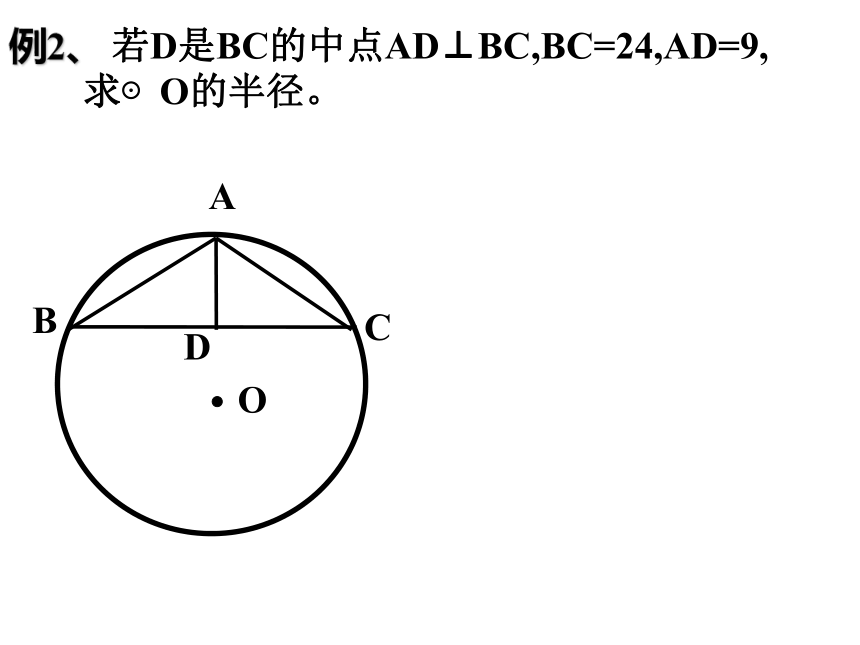
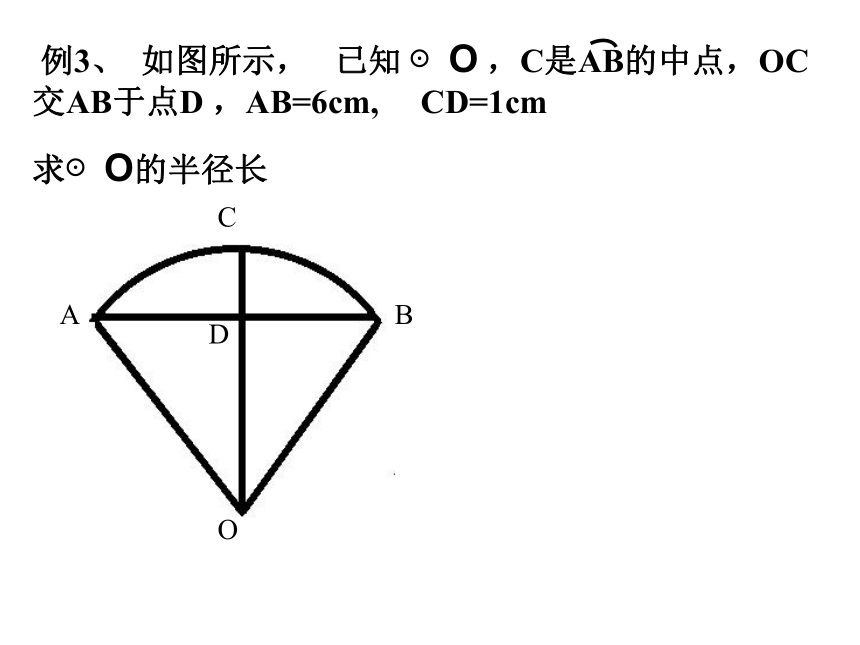
D.垂直于弦的直径平分这条弦。例2、 若D是BC的中点AD⊥BC,BC=24,AD=9, 求⊙O的半径。OABCD 例3、 如图所示, 已知 ⊙O ,C是AB的中点,OC交AB于点D ,AB=6cm, CD=1cm
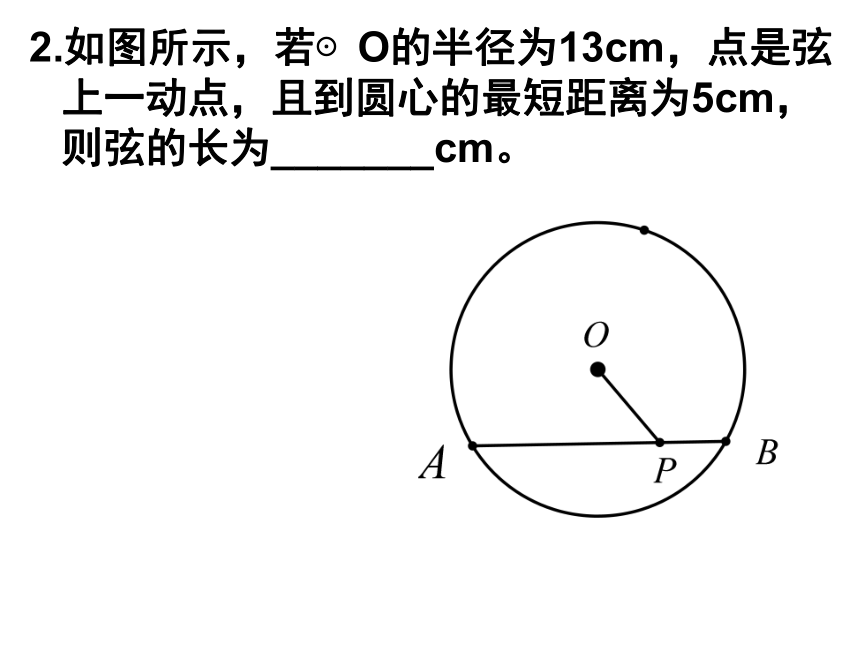
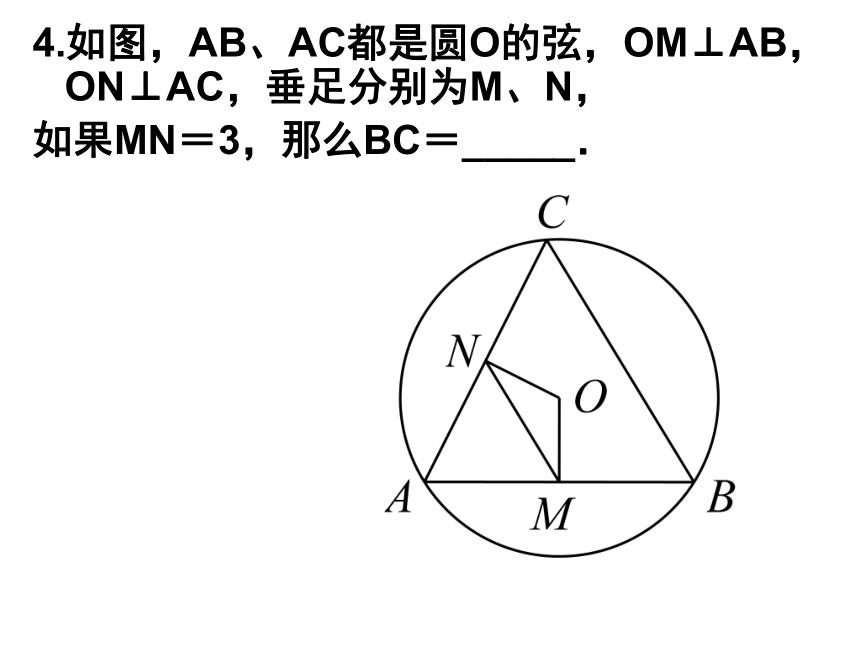
求⊙O的半径长2.如图所示,若⊙O的半径为13cm,点是弦上一动点,且到圆心的最短距离为5cm,则弦的长为_______cm。4.如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,
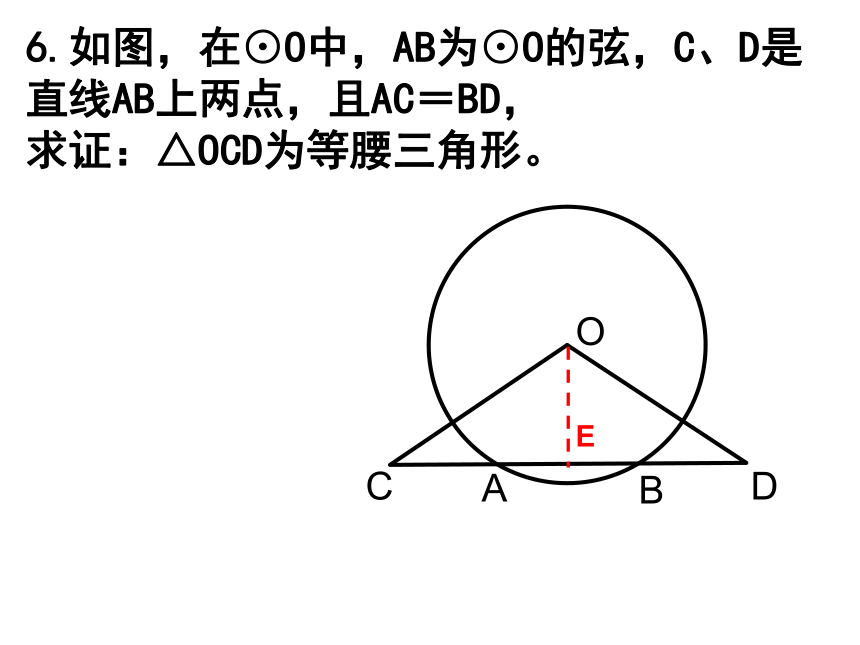
如果MN=3,那么BC=_____.6.如图,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD,
求证:△OCD为等腰三角形。 §3.2.2 圆的对称性学习目标:(1分钟)1.理解圆心角、弧、弦、弦心距之间的概念;
2.理解圆的对称性及相关性质。自学指导1:(4分钟)认真阅读P102-103的内容,注意理解:
1.圆的旋转不变性;
2.圆心角、弦、及弧之间相等关系的定理。2.圆是中心对称图形对称中心为圆心。 1.圆是轴对称图形,对称轴是任意一条过圆心的直线 点拨:3.圆心角:顶点在圆心,且与圆相交所形成的角,叫做圆心角。4.弦心距:OC圆心角、弧、弦、弦心距之间的关系在等圆中1.这两个相等的圆心角所对的弦分别是哪两条?它们相等吗?2.这两个相等的圆心角所对的弧分别是哪两条?它们相等吗?如果两个圆心角相等3.这两个相等的圆心角所对的弦心距相等吗?圆心角、弧、弦、弦心距之间的关系在同圆中,情况一样吗?圆心角、弧、弦、弦心距之间的关系在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,前提条件所对的弦心距相等。AB=CD ?在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。所对的弦心距相等。思考:在同圆内作两条长度相同的弦,它们所对的圆心角相等吗?所对的弧相等吗?圆心角、弧、弦、弦心距之间的关系在同圆或等圆中,如果两个圆心角、两条弧、两条弦、中有一组量相等,那么它们所对应的其余各组量都分别相等。两条弦心距1.如果两条弦相等,那么( )
A.这两条弦所对的弧相等
B.这两条弦所对的圆心角相等
C.这两条弦的弦心距相等
D.以上答案都不对自学检测1:(3分钟)2.完成P107的数学理解-2T;3. (2012陕西)如图,在半径为5的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为 .自学指导2:(4分钟)1.阅读P104-105的例2,注意:解题方法解题格式。2.仿例题,完成P107的知识技能-1T;??自学检测2:(5分钟)1.完成P107的数学理解-3T;2.如图:已知AB.CD是⊙O两条直径,弦CE∥AB,弧EC的度数为40°,则∠BOC=______ABCDEO3.如图, ⊙O中弦AB⊥AC,D,E分别是AB,AC的中点.若AB=AC,则四边形OEAD是 形。变式:完成P106的随堂练习-3T当堂训练:(8分钟)1.⊙O中,弦AB的长恰等于半径,则弦AB所对圆心角是 度.3.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的直径的长为 。 2.在半径为2cm的⊙O中有长为2 cm的弦AB,则弦AB所对的圆心角的度数为 . 4.(2012内蒙古)如图,AB是⊙O的直径,点C、D在⊙O上 ,∠BOD=110°,AC∥OD,则∠AOC的度数( )
A. 70° B. 60° C. 50° D. 40°5.如图,A是半径为5的⊙O内一点,且OA=3,过点A且长小于8的弦有( )
A.0条 B.1条 C.2条 D.4条变式:过点A且长小于10的整数弦的条数为 条。 6.如图,有一座石拱桥的桥拱是以为圆心,为半径的一段圆弧.若 ,OA=4m,请求出石拱桥的高度.
条直线垂直这条弦。???(4)平分劣弧的直线,平分这条弧所对的 弦。?变式训练:1.下列说法中,不成立的是 ( )
A.弦的垂直平分线必过圆心。
B.弦(不是直径)的中点与圆心的连线垂直平分这条弦。
C.垂直于弦的直线经过圆心,且平分这条弦所对的弧。
D.垂直于弦的直径平分这条弦。例2、 若D是BC的中点AD⊥BC,BC=24,AD=9, 求⊙O的半径。OABCD 例3、 如图所示, 已知 ⊙O ,C是AB的中点,OC交AB于点D ,AB=6cm, CD=1cm
求⊙O的半径长2.如图所示,若⊙O的半径为13cm,点是弦上一动点,且到圆心的最短距离为5cm,则弦的长为_______cm。4.如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,
如果MN=3,那么BC=_____.6.如图,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD,
求证:△OCD为等腰三角形。 §3.2.2 圆的对称性学习目标:(1分钟)1.理解圆心角、弧、弦、弦心距之间的概念;
2.理解圆的对称性及相关性质。自学指导1:(4分钟)认真阅读P102-103的内容,注意理解:
1.圆的旋转不变性;
2.圆心角、弦、及弧之间相等关系的定理。2.圆是中心对称图形对称中心为圆心。 1.圆是轴对称图形,对称轴是任意一条过圆心的直线 点拨:3.圆心角:顶点在圆心,且与圆相交所形成的角,叫做圆心角。4.弦心距:OC圆心角、弧、弦、弦心距之间的关系在等圆中1.这两个相等的圆心角所对的弦分别是哪两条?它们相等吗?2.这两个相等的圆心角所对的弧分别是哪两条?它们相等吗?如果两个圆心角相等3.这两个相等的圆心角所对的弦心距相等吗?圆心角、弧、弦、弦心距之间的关系在同圆中,情况一样吗?圆心角、弧、弦、弦心距之间的关系在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,前提条件所对的弦心距相等。AB=CD ?在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。所对的弦心距相等。思考:在同圆内作两条长度相同的弦,它们所对的圆心角相等吗?所对的弧相等吗?圆心角、弧、弦、弦心距之间的关系在同圆或等圆中,如果两个圆心角、两条弧、两条弦、中有一组量相等,那么它们所对应的其余各组量都分别相等。两条弦心距1.如果两条弦相等,那么( )
A.这两条弦所对的弧相等
B.这两条弦所对的圆心角相等
C.这两条弦的弦心距相等
D.以上答案都不对自学检测1:(3分钟)2.完成P107的数学理解-2T;3. (2012陕西)如图,在半径为5的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为 .自学指导2:(4分钟)1.阅读P104-105的例2,注意:解题方法解题格式。2.仿例题,完成P107的知识技能-1T;??自学检测2:(5分钟)1.完成P107的数学理解-3T;2.如图:已知AB.CD是⊙O两条直径,弦CE∥AB,弧EC的度数为40°,则∠BOC=______ABCDEO3.如图, ⊙O中弦AB⊥AC,D,E分别是AB,AC的中点.若AB=AC,则四边形OEAD是 形。变式:完成P106的随堂练习-3T当堂训练:(8分钟)1.⊙O中,弦AB的长恰等于半径,则弦AB所对圆心角是 度.3.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的直径的长为 。 2.在半径为2cm的⊙O中有长为2 cm的弦AB,则弦AB所对的圆心角的度数为 . 4.(2012内蒙古)如图,AB是⊙O的直径,点C、D在⊙O上 ,∠BOD=110°,AC∥OD,则∠AOC的度数( )
A. 70° B. 60° C. 50° D. 40°5.如图,A是半径为5的⊙O内一点,且OA=3,过点A且长小于8的弦有( )
A.0条 B.1条 C.2条 D.4条变式:过点A且长小于10的整数弦的条数为 条。 6.如图,有一座石拱桥的桥拱是以为圆心,为半径的一段圆弧.若 ,OA=4m,请求出石拱桥的高度.
