九年级数学第一学期期末测试题
图片预览

文档简介
九年级数学第一学期期末测试题
一、选择题(本大题共l2小题,每小题3分,共36分。)。
1.下列图形中既是轴对称图形又是中心对称图形的是( )
2.下列命题中,真命题是( )
A、有两边相等的平行四边形是菱形
B、对角线垂直的四边形是菱形
C、一组对边平行,另一组对边相等的四边形是平行四边形
D、两条对角线相等的平行四边形是矩形
3.方程的根是( )
A、; B、,; C、,; D、,.
4.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线
交对角线AC于点F,E为垂足,连接DF.则∠CDF等于( )。
A.80° B.70° C.65° D.60°
5.如图,在矩形ABCD中,AB=3,AD=4,P为AD上
的一点,PE⊥OA ,PF⊥OD,垂足为E、F.,则
PE+PF的值为( )
A、 B、 C、 D、
6.你玩过万花筒吗?它是由三块等宽等长的玻璃片围成的。下图是看到的万花筒的一个图形,图中所有的小三角形均是全等的等边三角形,其中的
菱形AEFG可以看成是把菱形ABCD以A为中心( )。
A、顺时针旋转60°得到 B、顺时针旋转120°得到
C、逆时针旋转60°得到 D、逆时针旋转120°得到
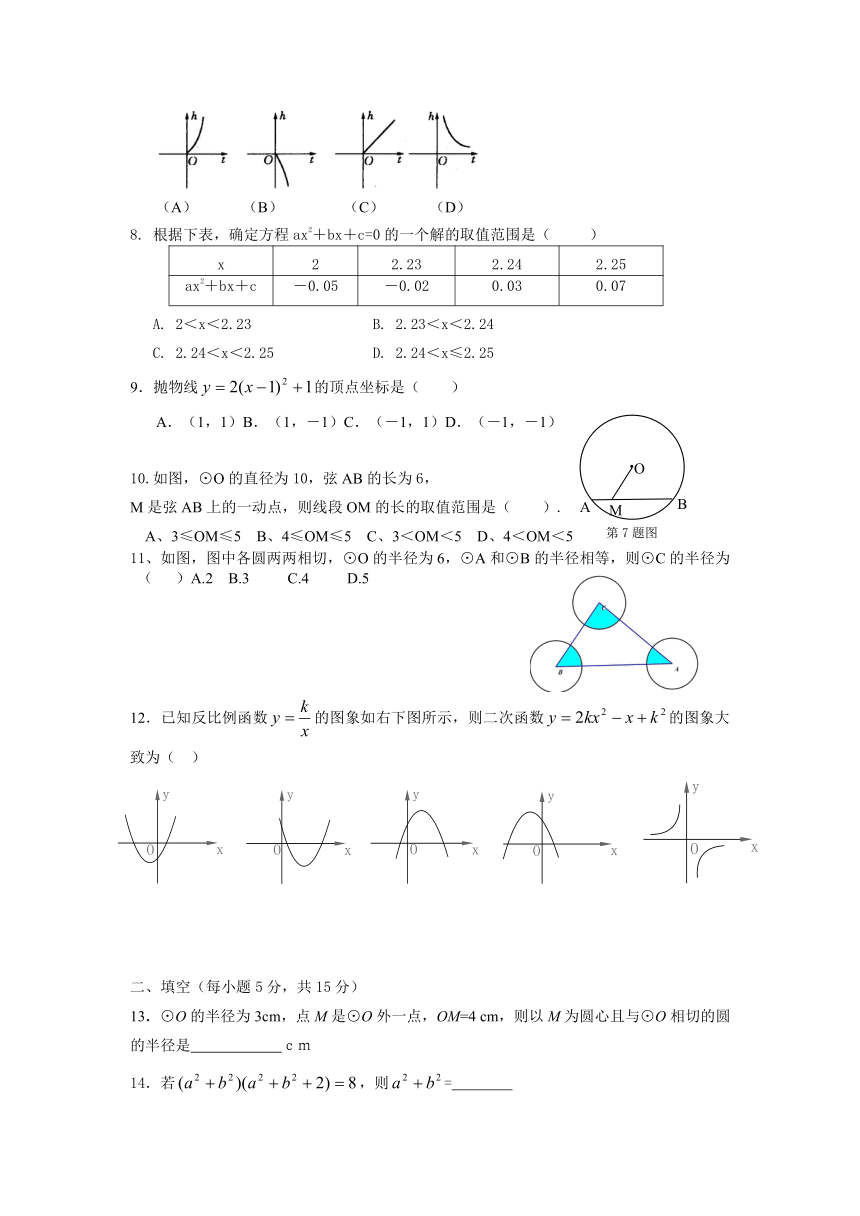
7.已知h关于t的函数关系式为,(g为正常数,t为时间),则函数图象为( ) (A) (B) (C) (D)
8. 根据下表,确定方程ax2+bx+c=0的一个解的取值范围是( )
x
2
2.23
2.24
2.25
ax2+bx+c
-0.05
-0.02
0.03
0.07
A. 2<x<2.23 B. 2.23<x<2.24
C. 2.24<x<2.25 D. 2.24<x≤2.25
9.抛物线的顶点坐标是( ) A.(1,1)B.(1,-1)C.(-1,1)D.(-1,-1)
10.如图,⊙O的直径为10,弦AB的长为6,
M是弦AB上的一动点,则线段OM的长的取值范围是( ).
A、3≤OM≤5 B、4≤OM≤5 C、3<OM<5 D、4<OM<5
11、如图,图中各圆两两相切,⊙O的半径为6,⊙A和⊙B的半径相等,则⊙C的半径为( )A.2 B.3 C.4 D.5
12.已知反比例函数的图象如右下图所示,则二次函数的图象大致为( )
二、填空(每小题5分,共15分)
13.⊙O的半径为3cm,点M是⊙O外一点,OM=4 cm,则以M为圆心且与⊙O相切的圆的半径是 cm
14.若,则=
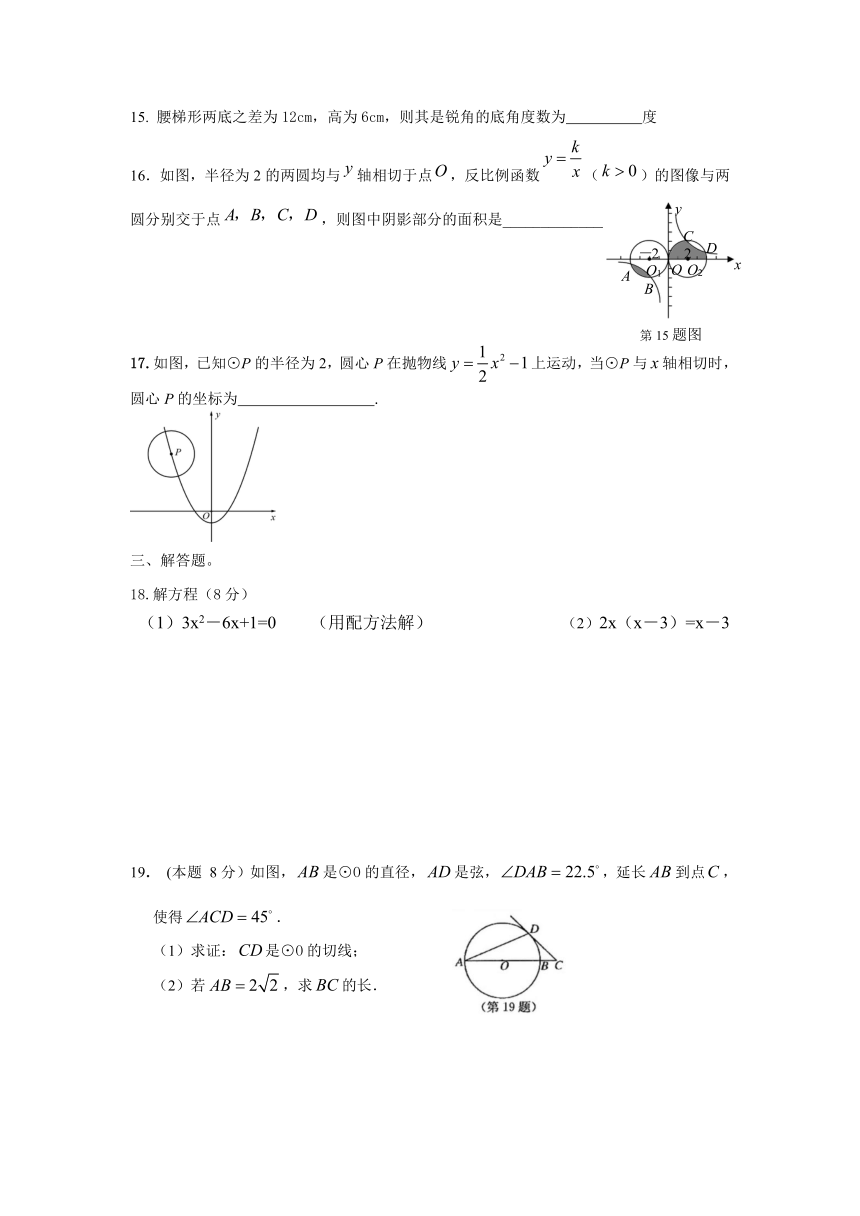
15. 腰梯形两底之差为12cm,高为6cm,则其是锐角的底角度数为 度
16.如图,半径为2的两圆均与轴相切于点,反比例函数()的图像与两圆分别交于点,则图中阴影部分的面积是________________。
17.如图,已知⊙P的半径为2,圆心P在抛物线上运动,当⊙P与轴相切时,圆心P的坐标为 .
三、解答题。
18.解方程(8分)
(1)3x2-6x+1=0 (用配方法解) (2)2x(x-3)=x-3
19. (本题 8分)如图,是⊙O的直径,是弦,,延长到点,使得.
(1)求证:是⊙O的切线;
(2)若,求的长.
20. (本题 8分)如图,在矩形ABCD中,AB=6,BC=8.,若将矩形折叠,使B点与D点重合,求折痕EF的长。
21.(本题 11分)如图21,一次函数的图象与反比例函数的图象交于A(-4,2)、B(2,n)两点,且与x轴交于点C。
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)根据图象写出一次函数的值小于反比例函数的值x的取值范围。
22.(本题 10分)已知:如图,在△ABC中,AB=AC,ADBC,垂足为D,AN
是△ABC外角CAM的平分线,CEAN,垂足为E,连接DE交AC于F。
(1)求证:四边形ADCE为矩形
(2)求证:DF∥AB,DF=AB
(3)当△ABC满足什么条件时,四边形ADCE是一个正方形?简述你的理由。
(第24题)
23.(本题 9分)如图,在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧BC上一点,连接BD,AD,OC,∠ADB=30°。
(1)求∠AOC的度数;(2)若弦BC=6cm,求图中阴影部分的面积。
24.(本题 12)某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
A型利润
B型利润
甲店
200
170
乙店
160
150
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的AB型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
一、选择题(本大题共l2小题,每小题3分,共36分。)。
1.下列图形中既是轴对称图形又是中心对称图形的是( )
2.下列命题中,真命题是( )
A、有两边相等的平行四边形是菱形
B、对角线垂直的四边形是菱形
C、一组对边平行,另一组对边相等的四边形是平行四边形
D、两条对角线相等的平行四边形是矩形
3.方程的根是( )
A、; B、,; C、,; D、,.
4.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线
交对角线AC于点F,E为垂足,连接DF.则∠CDF等于( )。
A.80° B.70° C.65° D.60°
5.如图,在矩形ABCD中,AB=3,AD=4,P为AD上
的一点,PE⊥OA ,PF⊥OD,垂足为E、F.,则
PE+PF的值为( )
A、 B、 C、 D、
6.你玩过万花筒吗?它是由三块等宽等长的玻璃片围成的。下图是看到的万花筒的一个图形,图中所有的小三角形均是全等的等边三角形,其中的
菱形AEFG可以看成是把菱形ABCD以A为中心( )。
A、顺时针旋转60°得到 B、顺时针旋转120°得到
C、逆时针旋转60°得到 D、逆时针旋转120°得到
7.已知h关于t的函数关系式为,(g为正常数,t为时间),则函数图象为( ) (A) (B) (C) (D)
8. 根据下表,确定方程ax2+bx+c=0的一个解的取值范围是( )
x
2
2.23
2.24
2.25
ax2+bx+c
-0.05
-0.02
0.03
0.07
A. 2<x<2.23 B. 2.23<x<2.24
C. 2.24<x<2.25 D. 2.24<x≤2.25
9.抛物线的顶点坐标是( ) A.(1,1)B.(1,-1)C.(-1,1)D.(-1,-1)
10.如图,⊙O的直径为10,弦AB的长为6,
M是弦AB上的一动点,则线段OM的长的取值范围是( ).
A、3≤OM≤5 B、4≤OM≤5 C、3<OM<5 D、4<OM<5
11、如图,图中各圆两两相切,⊙O的半径为6,⊙A和⊙B的半径相等,则⊙C的半径为( )A.2 B.3 C.4 D.5
12.已知反比例函数的图象如右下图所示,则二次函数的图象大致为( )
二、填空(每小题5分,共15分)
13.⊙O的半径为3cm,点M是⊙O外一点,OM=4 cm,则以M为圆心且与⊙O相切的圆的半径是 cm
14.若,则=
15. 腰梯形两底之差为12cm,高为6cm,则其是锐角的底角度数为 度
16.如图,半径为2的两圆均与轴相切于点,反比例函数()的图像与两圆分别交于点,则图中阴影部分的面积是________________。
17.如图,已知⊙P的半径为2,圆心P在抛物线上运动,当⊙P与轴相切时,圆心P的坐标为 .
三、解答题。
18.解方程(8分)
(1)3x2-6x+1=0 (用配方法解) (2)2x(x-3)=x-3
19. (本题 8分)如图,是⊙O的直径,是弦,,延长到点,使得.
(1)求证:是⊙O的切线;
(2)若,求的长.
20. (本题 8分)如图,在矩形ABCD中,AB=6,BC=8.,若将矩形折叠,使B点与D点重合,求折痕EF的长。
21.(本题 11分)如图21,一次函数的图象与反比例函数的图象交于A(-4,2)、B(2,n)两点,且与x轴交于点C。
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)根据图象写出一次函数的值小于反比例函数的值x的取值范围。
22.(本题 10分)已知:如图,在△ABC中,AB=AC,ADBC,垂足为D,AN
是△ABC外角CAM的平分线,CEAN,垂足为E,连接DE交AC于F。
(1)求证:四边形ADCE为矩形
(2)求证:DF∥AB,DF=AB
(3)当△ABC满足什么条件时,四边形ADCE是一个正方形?简述你的理由。
(第24题)
23.(本题 9分)如图,在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧BC上一点,连接BD,AD,OC,∠ADB=30°。
(1)求∠AOC的度数;(2)若弦BC=6cm,求图中阴影部分的面积。
24.(本题 12)某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
A型利润
B型利润
甲店
200
170
乙店
160
150
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的AB型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
同课章节目录
