第十章 全等三角形的性质与判定的综合应用 专题训练(含答案)
文档属性
| 名称 | 第十章 全等三角形的性质与判定的综合应用 专题训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题训练
全等三角形的性质与判定的综合应用
类型一 求角的度数
1.如图,BC∥EF,BC=BE,AB=FB,∠1=∠2.若∠1=55°,则∠C的度数为( )
A.25° B.55° C.45° D.35°
第1题图 第2题图
2.如图,以△ABC的顶点A为圆心,BC长为半径作弧;再以顶点C为圆心,AB长为半径作弧,两弧交于点D.连接AD,CD.若∠B=55°,则∠ADC的度数为___________.
3.如图,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
类型二 求线段的长度
4.如图,在△ABC中,∠CAD=∠EAD,∠ADC=∠ADE.若CB=5cm,BD=3cm,则ED的长为( )
A.2 cm B.3 cm C.5 cm D.8 cm
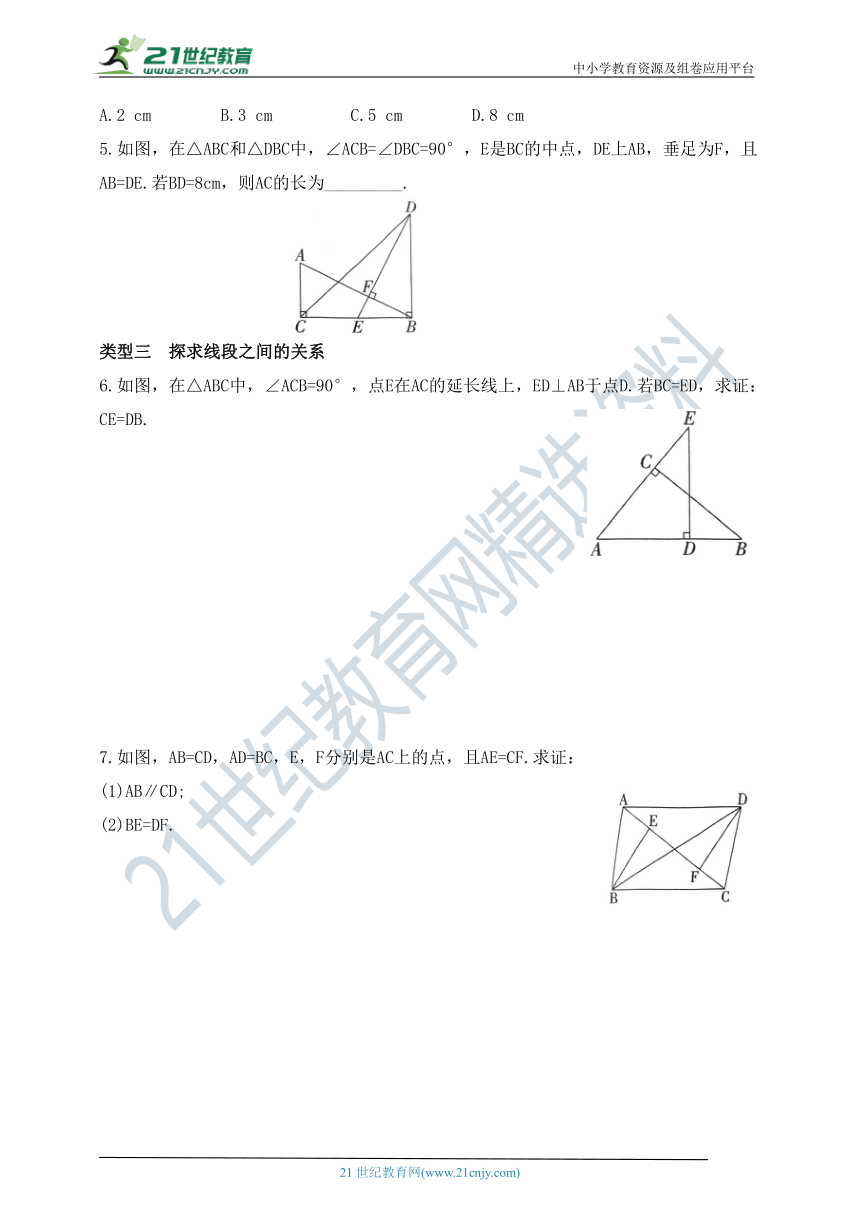
5.如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE上AB,垂足为F,且
AB=DE.若BD=8cm,则AC的长为_________.
类型三 探求线段之间的关系
6.如图,在△ABC中,∠ACB=90°,点E在AC的延长线上,ED⊥AB于点D.若BC=ED,求证:CE=DB.
7.如图,AB=CD,AD=BC,E,F分别是AC上的点,且AE=CF.求证:
(1)AB∥CD;
(2)BE=DF.
8.如图,在四边形ABCD中,AD∥BC,E是CD的中点,连接AE,BE,延长AE交BC的延长线于
点F.
(1)△DAE与△CFE全等吗 请说明理由.
(2)若AB=BC+AD,求证:BE⊥AF.
类型四 构造全等三角形
9.(1)如图①,在△ABC中,若AB=10,BC=8,求边AC上的中线BD的取值范围.小聪同学是这样思考的:延长BD至点E,使DE=BD,连接CE,利用全等将边AB转化为CE,在△BCE 中利用三角形的三边关系即可求出中线BD的取值范围.在这个过程中,小聪同学证三角形全等用到的判定方法是________________,中线BD的取值范围是______________.
(2)如图②,在△ABC中,D是AC的中点,点M在边AB上,点N在边BC上,且DM⊥DN.求证:AM+CN>MN.
10.如图,在△ABC中,∠A=100°,∠ABC=40°,BD是△ABC的角平分线.延长BD至点E,
使DE=AD,连接EC
(1)∠CDE=___________;
(2)猜想线段BC与AB+CE的数量关系,并说明理由.
参考答案
1.B 2. 55
3.(1)在△BEF和△CDA中,∴△BEF≌△CDA.∴∠D=∠2
(2)∵∠D=∠2,∠D=78°,∴∠2=78°.∵EF∥AC,∴∠BAC=∠2=78°
4.A 5. 4 cm
6.∵ED⊥AB,∠ACB=90°,∴∠ADE=∠ACB=90°.∵∠A=∠A,ED=BC,∴△AED≌ABC.∴AE=AB,AD=AC.∴AE-AC=AB-AD,即CE=DB
7.(1)在△ABD和△CDB中, ∴△ABD≌△CDB.∴∠ABD=∠CDB.∴AB∥CD
(2)由(1),知AB∥CD,∴∠BAE=∠DCF.在△ABE和△CDF中,
∴△ABE≌△CDF.∴BE=DF
8.(1)△DAE≌△CFE 理由:∵AD∥BC,∴∠ADE=∠FCE.∵E是CD的中点,∴DE=CE.
在△DAE和△CFE中,∴△DAE≌△CFE.
(2)由(1),知△DAE≌△CFE,∴AE=FE,AD=FC.∴AB=BC+AD=BC+CF=BF.
在△ABE和△FBE中,∴△ABE≌△FBE.∴∠AEB=∠FEB.
又∵∠AEB+∠FEB=180°,∴∠AEB=90°,即BE⊥AF
9.(1)SAS 1<BD<9
(2)延长ND至点F,使FD=ND,连接AF,MF.同(1),得△AFD≌△CND,∴AF=CN.
∵DM⊥DN,∴∠FDM=∠NDM=90°.在△MDN和△MDF中,∴△MDN≌△MDF.
∴MN=MF.在△AFM中,由三角形的三边关系,得AM+AF>MF,∴AM+CN>MN
10.(1)60°
(2)BC=AB+CE 理由:在BC上截取BF=AB,连接DF.∵BD平分∠ABC,∴∠ABD=∠FBD.
在△ABD和△FBD中,∴△ABD≌△FBD.∴DF=DA=DE,∠FDB=∠ADB=∠CDE=60°.∴∠FDC=180°-∠ADB-∠BDF=60°=∠EDC.
在△CDF和△CDE中, ∴△CDF≌△CDE,∴CF=CE.∴BC=BF+CF=AB+CE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题训练
全等三角形的性质与判定的综合应用
类型一 求角的度数
1.如图,BC∥EF,BC=BE,AB=FB,∠1=∠2.若∠1=55°,则∠C的度数为( )
A.25° B.55° C.45° D.35°
第1题图 第2题图
2.如图,以△ABC的顶点A为圆心,BC长为半径作弧;再以顶点C为圆心,AB长为半径作弧,两弧交于点D.连接AD,CD.若∠B=55°,则∠ADC的度数为___________.
3.如图,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
类型二 求线段的长度
4.如图,在△ABC中,∠CAD=∠EAD,∠ADC=∠ADE.若CB=5cm,BD=3cm,则ED的长为( )
A.2 cm B.3 cm C.5 cm D.8 cm
5.如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE上AB,垂足为F,且
AB=DE.若BD=8cm,则AC的长为_________.
类型三 探求线段之间的关系
6.如图,在△ABC中,∠ACB=90°,点E在AC的延长线上,ED⊥AB于点D.若BC=ED,求证:CE=DB.
7.如图,AB=CD,AD=BC,E,F分别是AC上的点,且AE=CF.求证:
(1)AB∥CD;
(2)BE=DF.
8.如图,在四边形ABCD中,AD∥BC,E是CD的中点,连接AE,BE,延长AE交BC的延长线于
点F.
(1)△DAE与△CFE全等吗 请说明理由.
(2)若AB=BC+AD,求证:BE⊥AF.
类型四 构造全等三角形
9.(1)如图①,在△ABC中,若AB=10,BC=8,求边AC上的中线BD的取值范围.小聪同学是这样思考的:延长BD至点E,使DE=BD,连接CE,利用全等将边AB转化为CE,在△BCE 中利用三角形的三边关系即可求出中线BD的取值范围.在这个过程中,小聪同学证三角形全等用到的判定方法是________________,中线BD的取值范围是______________.
(2)如图②,在△ABC中,D是AC的中点,点M在边AB上,点N在边BC上,且DM⊥DN.求证:AM+CN>MN.
10.如图,在△ABC中,∠A=100°,∠ABC=40°,BD是△ABC的角平分线.延长BD至点E,
使DE=AD,连接EC
(1)∠CDE=___________;
(2)猜想线段BC与AB+CE的数量关系,并说明理由.
参考答案
1.B 2. 55
3.(1)在△BEF和△CDA中,∴△BEF≌△CDA.∴∠D=∠2
(2)∵∠D=∠2,∠D=78°,∴∠2=78°.∵EF∥AC,∴∠BAC=∠2=78°
4.A 5. 4 cm
6.∵ED⊥AB,∠ACB=90°,∴∠ADE=∠ACB=90°.∵∠A=∠A,ED=BC,∴△AED≌ABC.∴AE=AB,AD=AC.∴AE-AC=AB-AD,即CE=DB
7.(1)在△ABD和△CDB中, ∴△ABD≌△CDB.∴∠ABD=∠CDB.∴AB∥CD
(2)由(1),知AB∥CD,∴∠BAE=∠DCF.在△ABE和△CDF中,
∴△ABE≌△CDF.∴BE=DF
8.(1)△DAE≌△CFE 理由:∵AD∥BC,∴∠ADE=∠FCE.∵E是CD的中点,∴DE=CE.
在△DAE和△CFE中,∴△DAE≌△CFE.
(2)由(1),知△DAE≌△CFE,∴AE=FE,AD=FC.∴AB=BC+AD=BC+CF=BF.
在△ABE和△FBE中,∴△ABE≌△FBE.∴∠AEB=∠FEB.
又∵∠AEB+∠FEB=180°,∴∠AEB=90°,即BE⊥AF
9.(1)SAS 1<BD<9
(2)延长ND至点F,使FD=ND,连接AF,MF.同(1),得△AFD≌△CND,∴AF=CN.
∵DM⊥DN,∴∠FDM=∠NDM=90°.在△MDN和△MDF中,∴△MDN≌△MDF.
∴MN=MF.在△AFM中,由三角形的三边关系,得AM+AF>MF,∴AM+CN>MN
10.(1)60°
(2)BC=AB+CE 理由:在BC上截取BF=AB,连接DF.∵BD平分∠ABC,∴∠ABD=∠FBD.
在△ABD和△FBD中,∴△ABD≌△FBD.∴DF=DA=DE,∠FDB=∠ADB=∠CDE=60°.∴∠FDC=180°-∠ADB-∠BDF=60°=∠EDC.
在△CDF和△CDE中, ∴△CDF≌△CDE,∴CF=CE.∴BC=BF+CF=AB+CE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
