人教版八年级数学下册 第十七章 勾股定理的探究 教案(表格式)
文档属性
| 名称 | 人教版八年级数学下册 第十七章 勾股定理的探究 教案(表格式) |  | |
| 格式 | doc | ||
| 文件大小 | 277.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 10:41:26 | ||
图片预览


文档简介
勾股定理活动探究的教学设计
第十七章 勾股定理的探究
【教材】 人教版八年级数学下册第36页. 【课时安排】 1个课时
【教学对象】 八年级(下)学生.【授课教师】 武鸣区双桥中心学校 黄金凤
【教学目标】
知识与技能
( 1 ) 通过拼图活动,培养学生的动手操作能力和决实际问题。
(2)了解勾股定理的文化背景,体验勾股定理探索过程。
过程与方法
(1)通过拼图活动,体验数学思维的严谨性,发展形象思维.
(2)在勾股定理的探索过程中,发展合情推理能力,体会数形结合思想.
情感态度价值观
纠正片面观点: “数学只是一些枯燥的公式、规定,没有什么实际意义!学了数学没有用!”体会数学源于实际,高于实际,运用于实际的科学价值与文化价值。
【教学重点】 1. 理解勾股定理的证明;2. 运用勾股定理解决具体问题。
【教学难点】利用“拼图”、“数形结合”的方法验证勾股定理中的解题思路是什,
【教学方法】观察法、小组讨论法、启发式教学法。
【教学手段】 拼图
【教学过程设计】
教学流程设计
二、教学过程设计
教学环节 教 学 内 容 教师活动 学生活动 设 计 意 图
(一)创设情景,引入活动约5分钟 【伽菲尔德证明勾股定理 ( http: / / www. / s q=%E5%8B%BE%E8%82%A1%E5%AE%9A%E7%90%86&ie=utf-8&src=wenda_link )的故事 ( http: / / www. / s q=%E6%95%85%E4%BA%8B&ie=utf-8&src=wenda_link )】
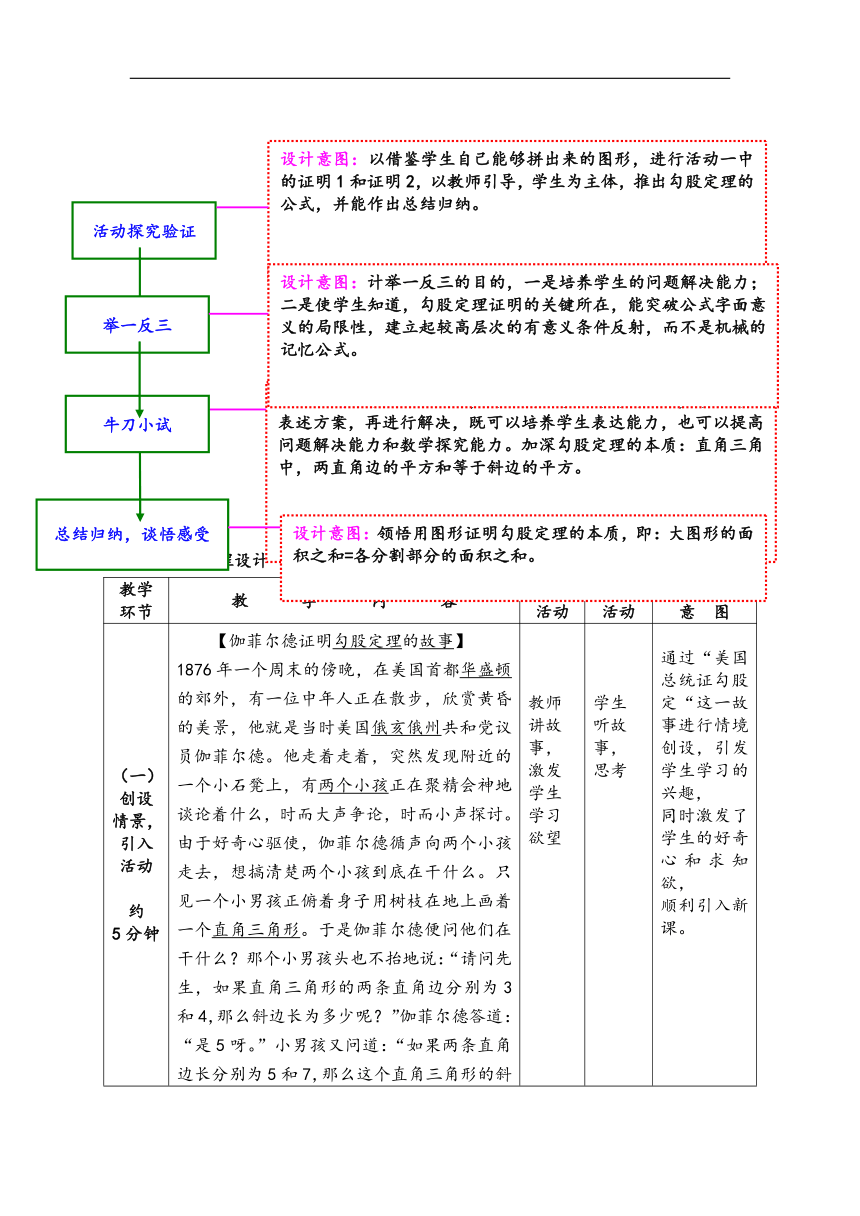
1876年一个周末的傍晚,在美国首都华盛顿 ( http: / / www. / s q=%E5%8D%8E%E7%9B%9B%E9%A1%BF&ie=utf-8&src=wenda_link )的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州 ( http: / / www. / s q=%E4%BF%84%E4%BA%A5%E4%BF%84%E5%B7%9E&ie=utf-8&src=wenda_link )共和党议员伽菲尔德。他走着走着,突然发现附近的一个小石凳上,有两个小孩 ( http: / / www. / s q=%E4%B8%A4%E4%B8%AA%E5%B0%8F%E5%AD%A9&ie=utf-8&src=wenda_link )正在聚精会神地谈论着什么,时而大声争论,时而小声探讨。由于好奇心驱使,伽菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形 ( http: / / www. / s q=%E7%9B%B4%E8%A7%92%E4%B8%89%E8%A7%92%E5%BD%A2&ie=utf-8&src=wenda_link )。于是伽菲尔德便问他们在干什么?那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”伽菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边长分别为5和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不假思索地回答道:“那斜边的平方一定等于5的平方加上7的平方。”小男孩又说:“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无法解释了,心里很不是滋味。
于是,伽菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法。 教师讲故事,激发学生学习欲望 学生听故事,思考 通过“美国总统证勾股定“这一故事进行情境创设,引发学生学习的兴趣,同时激发了学生的好奇心和求知欲,顺利引入新课。
(二)动手操作约10分钟 活动一:用四张全等的直角三角形纸片拼含有正方形的图案,要求拼图时直角三角形纸片不能互相重叠. 教师发出指令引导学生操作 学生动手操作上台展示成果 让学生根据正方形四条边的长度相等,自己动手演算进行拼图,积极思考,尝试各种拼法,为后面的证明过程做好准备。
(三)实验探究证明约10分钟 证明1该图为2002年8月在北京召开的国际数学家大会的会徽示意图,取材于我国古代数学著作《勾股圆方图》.大正方形的面积可以表示为 ______;也可以表示为 __________________ ∵ c2= =b2-2ab+a2+ 2ab =a2+b2, ∴a2+b2=c2证明2大正方形的面积可以表示为 _________ 也可以表示为_____________∵ (a+b)2 = c2 a2+2ab+b2 = 2ab +c2 , ∴a2+b2=c2 . 教师以设计问题填空的形式,引导学生去思考,进行分析列等式。进行分析讲解 学生思考识别解决问题学生思考回答问题 . 根据学生拼出的不同图形进行分析,强化勾股定理证明过程中的本质:分割的各面积之和=大正方形的面积。
(四)举一反三约8分钟 活动二证明3:你能只用这两个直角三角形说明a2+b2=c2? 对比两个图形,你能直接观察验证出勾股定理吗? a2 + b2 = c2 教师演示教师演示 学生观察思考领悟并发表见解学生观察思考领悟并发表见解 设计举一反三的目的,一是培养学生的问题解决能力;二是使学生知道,公式的本质所在,能突破公式字面意义的局限性,建立起较高层次的有意义条件反射,而不是机械的记忆公式。
(五)牛刀小试约7分钟 活动三学校需要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.请你应用勾股定理提出一个解决这个问题的方案,并与同伴交流.由学生先想出具体的计算方案教师把问题具体化,提问,若把绳子拉开后,测得BC的长度等于3,绳子比旗杆长1米,如何计算? 教师引导学生解决问题 学生思考体会 学生把问题转化为直角三角形来解决,可以很快利角勾定理解相关的问题。
(六)总结归纳谈悟感受约5分钟 勾股定理从边的角度刻画了直角三角形的又一个特征. 人类对勾股定理的研究已有近3 000年的历史,在西方,勾股定理又被称为“毕达哥拉斯定理” “百牛定理” “驴桥定理”等等 .1.如何利用勾股定理解决实际生活中的具体问题?关键是什么?2.通过对勾股定理证明的探索,谈一谈你对证明勾股定理的感受. 教师与学生共同总结 学生谈谈自己的感悟 解决实际问题的关键是把之转化为直角三角形。
设计意图:通过课前小故事,讲述美国第二十任总统伽菲尔德要去证明勾股定理的缘由,能够让学生在动机上做好准备,对所学内容产生兴趣,使学生在活动前处于对知识的“饥饿状态”,产生一个心理“缺口”,从而激发学生产生弥合心理缺口的学习动力。
创设情景,引入活动
“绝招”
设计意图:现代学习方式的基本特征包括“体验性”,强调学生亲身去经历、去感悟。让学生通过自己动手拼图,体会到乐趣,从而找出数学表示、推导演算,体现“做数学”的现代数学教育理念。
动手操作
设计意图:以借鉴学生自己能够拼出来的图形,进行活动一中的证明1和证明2,以教师引导,学生为主体,推出勾股定理的公式,并能作出总结归纳。
活动探究验证
设计意图:计举一反三的目的,一是培养学生的问题解决能力;二是使学生知道,勾股定理证明的关键所在,能突破公式字面意义的局限性,建立起较高层次的有意义条件反射,而不是机械的记忆公式。
举一反三
设计意图:根据勾股定理,解决实际中旗杆高度问题,学生自己表述方案,再进行解决,既可以培养学生表达能力,也可以提高问题解决能力和数学探究能力。加深勾股定理的本质:直角三角中,两直角边的平方和等于斜边的平方。
牛刀小试
总结归纳,谈悟感受
设计意图:领悟用图形证明勾股定理的本质,即:大图形的面积之和=各分割部分的面积之和。
第十七章 勾股定理的探究
【教材】 人教版八年级数学下册第36页. 【课时安排】 1个课时
【教学对象】 八年级(下)学生.【授课教师】 武鸣区双桥中心学校 黄金凤
【教学目标】
知识与技能
( 1 ) 通过拼图活动,培养学生的动手操作能力和决实际问题。
(2)了解勾股定理的文化背景,体验勾股定理探索过程。
过程与方法
(1)通过拼图活动,体验数学思维的严谨性,发展形象思维.
(2)在勾股定理的探索过程中,发展合情推理能力,体会数形结合思想.
情感态度价值观
纠正片面观点: “数学只是一些枯燥的公式、规定,没有什么实际意义!学了数学没有用!”体会数学源于实际,高于实际,运用于实际的科学价值与文化价值。
【教学重点】 1. 理解勾股定理的证明;2. 运用勾股定理解决具体问题。
【教学难点】利用“拼图”、“数形结合”的方法验证勾股定理中的解题思路是什,
【教学方法】观察法、小组讨论法、启发式教学法。
【教学手段】 拼图
【教学过程设计】
教学流程设计
二、教学过程设计
教学环节 教 学 内 容 教师活动 学生活动 设 计 意 图
(一)创设情景,引入活动约5分钟 【伽菲尔德证明勾股定理 ( http: / / www. / s q=%E5%8B%BE%E8%82%A1%E5%AE%9A%E7%90%86&ie=utf-8&src=wenda_link )的故事 ( http: / / www. / s q=%E6%95%85%E4%BA%8B&ie=utf-8&src=wenda_link )】
1876年一个周末的傍晚,在美国首都华盛顿 ( http: / / www. / s q=%E5%8D%8E%E7%9B%9B%E9%A1%BF&ie=utf-8&src=wenda_link )的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州 ( http: / / www. / s q=%E4%BF%84%E4%BA%A5%E4%BF%84%E5%B7%9E&ie=utf-8&src=wenda_link )共和党议员伽菲尔德。他走着走着,突然发现附近的一个小石凳上,有两个小孩 ( http: / / www. / s q=%E4%B8%A4%E4%B8%AA%E5%B0%8F%E5%AD%A9&ie=utf-8&src=wenda_link )正在聚精会神地谈论着什么,时而大声争论,时而小声探讨。由于好奇心驱使,伽菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形 ( http: / / www. / s q=%E7%9B%B4%E8%A7%92%E4%B8%89%E8%A7%92%E5%BD%A2&ie=utf-8&src=wenda_link )。于是伽菲尔德便问他们在干什么?那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”伽菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边长分别为5和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不假思索地回答道:“那斜边的平方一定等于5的平方加上7的平方。”小男孩又说:“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无法解释了,心里很不是滋味。
于是,伽菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法。 教师讲故事,激发学生学习欲望 学生听故事,思考 通过“美国总统证勾股定“这一故事进行情境创设,引发学生学习的兴趣,同时激发了学生的好奇心和求知欲,顺利引入新课。
(二)动手操作约10分钟 活动一:用四张全等的直角三角形纸片拼含有正方形的图案,要求拼图时直角三角形纸片不能互相重叠. 教师发出指令引导学生操作 学生动手操作上台展示成果 让学生根据正方形四条边的长度相等,自己动手演算进行拼图,积极思考,尝试各种拼法,为后面的证明过程做好准备。
(三)实验探究证明约10分钟 证明1该图为2002年8月在北京召开的国际数学家大会的会徽示意图,取材于我国古代数学著作《勾股圆方图》.大正方形的面积可以表示为 ______;也可以表示为 __________________ ∵ c2= =b2-2ab+a2+ 2ab =a2+b2, ∴a2+b2=c2证明2大正方形的面积可以表示为 _________ 也可以表示为_____________∵ (a+b)2 = c2 a2+2ab+b2 = 2ab +c2 , ∴a2+b2=c2 . 教师以设计问题填空的形式,引导学生去思考,进行分析列等式。进行分析讲解 学生思考识别解决问题学生思考回答问题 . 根据学生拼出的不同图形进行分析,强化勾股定理证明过程中的本质:分割的各面积之和=大正方形的面积。
(四)举一反三约8分钟 活动二证明3:你能只用这两个直角三角形说明a2+b2=c2? 对比两个图形,你能直接观察验证出勾股定理吗? a2 + b2 = c2 教师演示教师演示 学生观察思考领悟并发表见解学生观察思考领悟并发表见解 设计举一反三的目的,一是培养学生的问题解决能力;二是使学生知道,公式的本质所在,能突破公式字面意义的局限性,建立起较高层次的有意义条件反射,而不是机械的记忆公式。
(五)牛刀小试约7分钟 活动三学校需要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.请你应用勾股定理提出一个解决这个问题的方案,并与同伴交流.由学生先想出具体的计算方案教师把问题具体化,提问,若把绳子拉开后,测得BC的长度等于3,绳子比旗杆长1米,如何计算? 教师引导学生解决问题 学生思考体会 学生把问题转化为直角三角形来解决,可以很快利角勾定理解相关的问题。
(六)总结归纳谈悟感受约5分钟 勾股定理从边的角度刻画了直角三角形的又一个特征. 人类对勾股定理的研究已有近3 000年的历史,在西方,勾股定理又被称为“毕达哥拉斯定理” “百牛定理” “驴桥定理”等等 .1.如何利用勾股定理解决实际生活中的具体问题?关键是什么?2.通过对勾股定理证明的探索,谈一谈你对证明勾股定理的感受. 教师与学生共同总结 学生谈谈自己的感悟 解决实际问题的关键是把之转化为直角三角形。
设计意图:通过课前小故事,讲述美国第二十任总统伽菲尔德要去证明勾股定理的缘由,能够让学生在动机上做好准备,对所学内容产生兴趣,使学生在活动前处于对知识的“饥饿状态”,产生一个心理“缺口”,从而激发学生产生弥合心理缺口的学习动力。
创设情景,引入活动
“绝招”
设计意图:现代学习方式的基本特征包括“体验性”,强调学生亲身去经历、去感悟。让学生通过自己动手拼图,体会到乐趣,从而找出数学表示、推导演算,体现“做数学”的现代数学教育理念。
动手操作
设计意图:以借鉴学生自己能够拼出来的图形,进行活动一中的证明1和证明2,以教师引导,学生为主体,推出勾股定理的公式,并能作出总结归纳。
活动探究验证
设计意图:计举一反三的目的,一是培养学生的问题解决能力;二是使学生知道,勾股定理证明的关键所在,能突破公式字面意义的局限性,建立起较高层次的有意义条件反射,而不是机械的记忆公式。
举一反三
设计意图:根据勾股定理,解决实际中旗杆高度问题,学生自己表述方案,再进行解决,既可以培养学生表达能力,也可以提高问题解决能力和数学探究能力。加深勾股定理的本质:直角三角中,两直角边的平方和等于斜边的平方。
牛刀小试
总结归纳,谈悟感受
设计意图:领悟用图形证明勾股定理的本质,即:大图形的面积之和=各分割部分的面积之和。
