青岛版(五四制)数学四年级下册 2.3 梯形的面积 课件(共22张PPT)
文档属性
| 名称 | 青岛版(五四制)数学四年级下册 2.3 梯形的面积 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 837.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
第2单元生活中的多边形
2.3 梯形的面积
学习目标
理解梯形面积计算公式的推导过程。
熟练运用转化的方法探索规律。
运用所学知识解决生活中梯形面积实际问题,发展空间概念 。
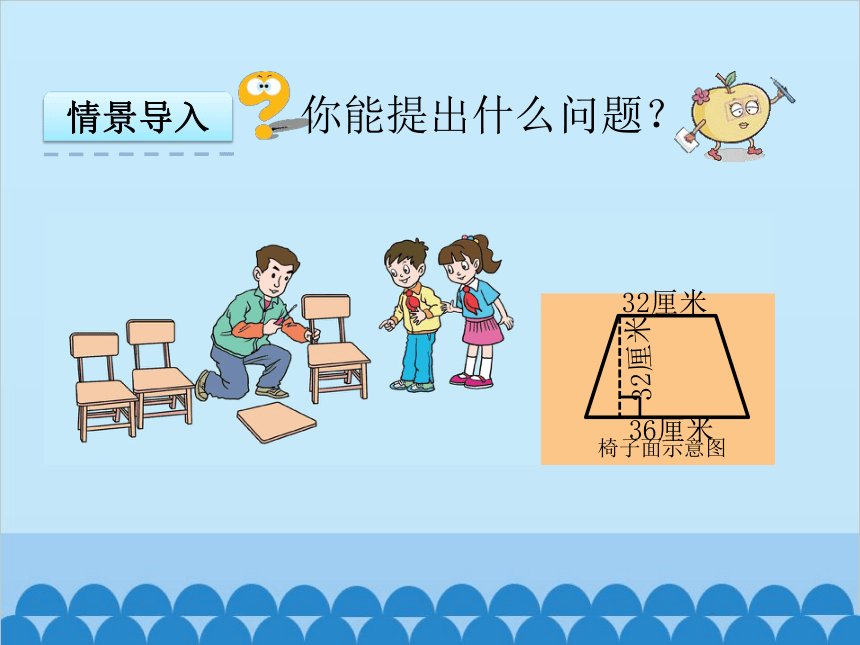
情景导入
椅子面示意图
36厘米
32厘米
32厘米
你能提出什么问题?
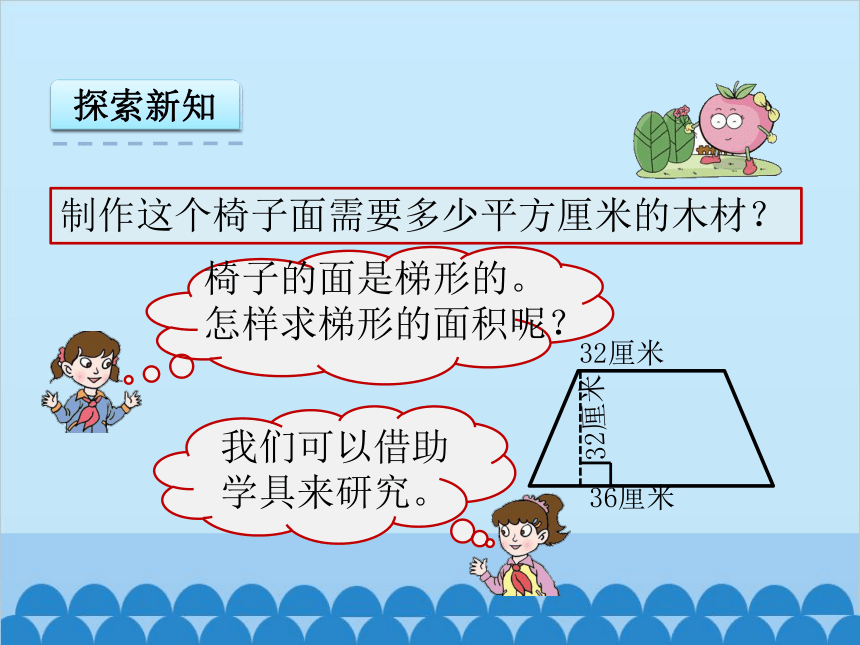
探索新知
制作这个椅子面需要多少平方厘米的木材?
椅子的面是梯形的。
怎样求梯形的面积呢?
36厘米
32厘米
32厘米
我们可以借助
学具来研究。
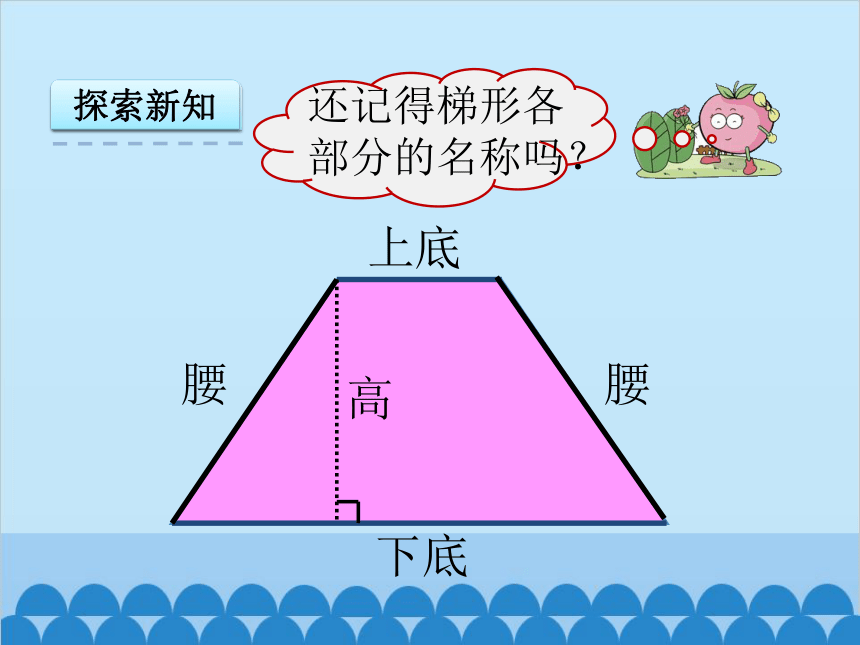
探索新知
上底
下底
腰
腰
高
还记得梯形各部分的名称吗?
探索新知
你能仿照求三角形面积的办法把梯形转化成已学过的图形,计算出它的面积吗?
拿出你的学具,拼拼看。
还有其它的拼法吗?试试看。
实验操作
想一想:
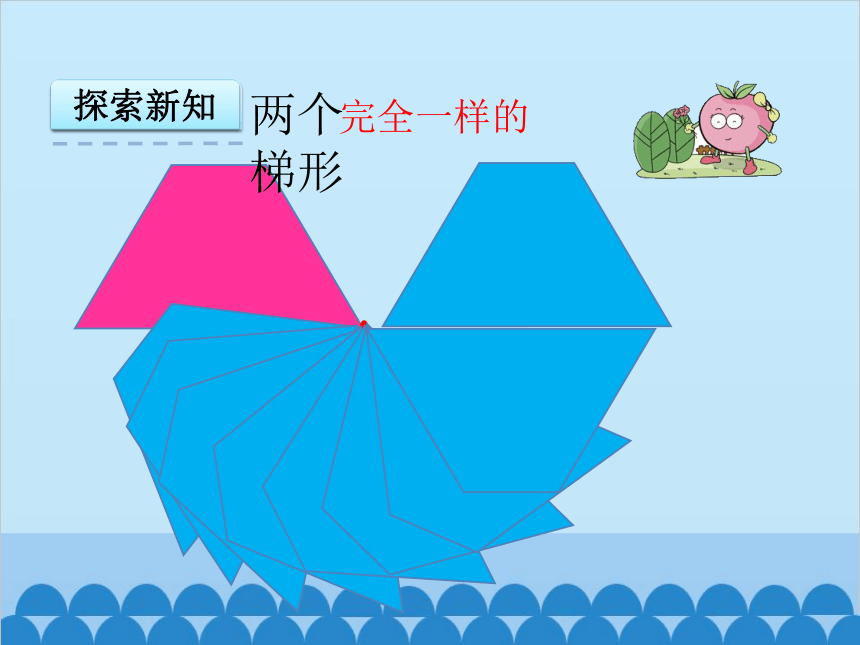
探索新知
两个 梯形
完全一样的
课堂小结
两个完全一样的梯形,可以拼成一个平行四边形。
探索新知
拼成的平行四边形与原来的梯形之间有怎样的关系?
探索新知
梯形的下底
梯形的上底
高
平行四边形的底
1.平行四边形的底与梯形的底有什么关系?
2.平行四边形的高与梯形的高有什么关系?
平行四边形的底等于梯形 的上底与下底的和。
平行四边形的高等于梯形的高。
探索新知
梯形的下底
梯形的上底
高
平行四边形的底
梯形面积= ÷2
平行四边形的面积
平行四边形的底×平行四边形的高
梯形上下底之和
梯形的高
梯形面积= × ÷2
课堂小结
梯形的面积=(上底+下底)×高÷2
用字母表示:S=(a + b )× h ÷2
典题精讲
你会求椅子面的面积吗?
S=(a + b )× h ÷2
=(32+36)×32÷2
椅子面示意图
36厘米
32厘米
32厘米
=68×32÷2
=1088(平方厘米)
答:制作这个椅子面需要1088平方厘米的木材。
一个鱼塘的形状是梯形,它的上底长21米,下底长45米,面积是759平方米。它的高是多少?(提示:用方程解。)
易错题型
21米
?米
米
45米
759平方米
解:设梯形鱼塘的高为xm。
根据S=(a+b)h列出方程
(21+45)×x=759
66x=759
x=759÷66
答:梯形鱼塘的高为11.5m 。
错误解答
x=11.5
一个鱼塘的形状是梯形,它的上底长21米,下底长45米,面积是759平方米。它的高是多少?(提示:用方程解。)
易错题型
21米
?米
米
45米
759平方米
解:设梯形鱼塘的高为xm。
根据S=(a+b)h÷2列出方程
(21+45)×x÷2=759
66x÷2=759
66x=759×2
答:梯形鱼塘的高为23m 。
正确解答
x=1518÷66
x=23
学以致用
1. 计算下面梯形的面积。
S=(a+b)×h÷2
=(4+8)×3÷2
=36÷2
=18cm2
S=(a+b)h÷2
=(6+10)×6÷2
=96÷2
=48dm2
4 cm
8 cm
3 cm
6 dm
6 dm
10 dm
学以致用
2. 某水渠的横截面是梯形(如
图)。渠口宽8米,渠底宽5
米,渠深1.8米。求它的横截
面面积。
S=(a+b)×h÷2
=(5+8)×1.8÷2
=23.4÷2
=16.2(平方米)
答:它的横截面面积为16.2平方米。
学以致用
3. 木材场常常把木材堆成下图的形状。在计算木材根数时通常
用下面的方法:
(1)请算出图中木材的根数。
(2)你能用梯形面积公式解释上面的算法吗?
(顶层根数+底层根数)×层数÷2
(3+6)×4÷2=18(根)
学以致用
4.
下底:
84-(19+24)=51(m)
面积:
S=(a+b)×h÷2
=(19+51)×24÷2
=70×24÷2
=70×12
=840m2
学以致用
5.
思路分析:
①算出三角形的高
=60×2÷15
=8(m)
h=2S÷a
②算出梯形的面积
S=(a+b)×h÷2
=(5+15)×8÷2
=20×8÷2
=20×4
=80m2
课堂小结
●这节课我学会了用( )方法
推导梯形的面积,在前面我还用这种方法推导出了( )和( )的面积。
●两个( )的梯形可以拼成一个平行四边形。这个平行四边形的底等于梯形的( )与( )的和,高等于梯形的( ),每个梯形的面积等于拼成的平行四边形面积的( )。
梯形面积用字母表示为( )。
完全一样
上底
下底
高
一半
S=(a+b)×h÷2
转化的
平行四边形
三角形
思维练习
在下图的梯形中,剪下一个最大的三角形,剩下的是什么图形?剩下的图形的面积是多少平方厘米?
25厘米
10厘米
15厘米
s=ah÷2
=15×10÷2
=15×5
=75(cm2)
第2单元生活中的多边形
2.3 梯形的面积
学习目标
理解梯形面积计算公式的推导过程。
熟练运用转化的方法探索规律。
运用所学知识解决生活中梯形面积实际问题,发展空间概念 。
情景导入
椅子面示意图
36厘米
32厘米
32厘米
你能提出什么问题?
探索新知
制作这个椅子面需要多少平方厘米的木材?
椅子的面是梯形的。
怎样求梯形的面积呢?
36厘米
32厘米
32厘米
我们可以借助
学具来研究。
探索新知
上底
下底
腰
腰
高
还记得梯形各部分的名称吗?
探索新知
你能仿照求三角形面积的办法把梯形转化成已学过的图形,计算出它的面积吗?
拿出你的学具,拼拼看。
还有其它的拼法吗?试试看。
实验操作
想一想:
探索新知
两个 梯形
完全一样的
课堂小结
两个完全一样的梯形,可以拼成一个平行四边形。
探索新知
拼成的平行四边形与原来的梯形之间有怎样的关系?
探索新知
梯形的下底
梯形的上底
高
平行四边形的底
1.平行四边形的底与梯形的底有什么关系?
2.平行四边形的高与梯形的高有什么关系?
平行四边形的底等于梯形 的上底与下底的和。
平行四边形的高等于梯形的高。
探索新知
梯形的下底
梯形的上底
高
平行四边形的底
梯形面积= ÷2
平行四边形的面积
平行四边形的底×平行四边形的高
梯形上下底之和
梯形的高
梯形面积= × ÷2
课堂小结
梯形的面积=(上底+下底)×高÷2
用字母表示:S=(a + b )× h ÷2
典题精讲
你会求椅子面的面积吗?
S=(a + b )× h ÷2
=(32+36)×32÷2
椅子面示意图
36厘米
32厘米
32厘米
=68×32÷2
=1088(平方厘米)
答:制作这个椅子面需要1088平方厘米的木材。
一个鱼塘的形状是梯形,它的上底长21米,下底长45米,面积是759平方米。它的高是多少?(提示:用方程解。)
易错题型
21米
?米
米
45米
759平方米
解:设梯形鱼塘的高为xm。
根据S=(a+b)h列出方程
(21+45)×x=759
66x=759
x=759÷66
答:梯形鱼塘的高为11.5m 。
错误解答
x=11.5
一个鱼塘的形状是梯形,它的上底长21米,下底长45米,面积是759平方米。它的高是多少?(提示:用方程解。)
易错题型
21米
?米
米
45米
759平方米
解:设梯形鱼塘的高为xm。
根据S=(a+b)h÷2列出方程
(21+45)×x÷2=759
66x÷2=759
66x=759×2
答:梯形鱼塘的高为23m 。
正确解答
x=1518÷66
x=23
学以致用
1. 计算下面梯形的面积。
S=(a+b)×h÷2
=(4+8)×3÷2
=36÷2
=18cm2
S=(a+b)h÷2
=(6+10)×6÷2
=96÷2
=48dm2
4 cm
8 cm
3 cm
6 dm
6 dm
10 dm
学以致用
2. 某水渠的横截面是梯形(如
图)。渠口宽8米,渠底宽5
米,渠深1.8米。求它的横截
面面积。
S=(a+b)×h÷2
=(5+8)×1.8÷2
=23.4÷2
=16.2(平方米)
答:它的横截面面积为16.2平方米。
学以致用
3. 木材场常常把木材堆成下图的形状。在计算木材根数时通常
用下面的方法:
(1)请算出图中木材的根数。
(2)你能用梯形面积公式解释上面的算法吗?
(顶层根数+底层根数)×层数÷2
(3+6)×4÷2=18(根)
学以致用
4.
下底:
84-(19+24)=51(m)
面积:
S=(a+b)×h÷2
=(19+51)×24÷2
=70×24÷2
=70×12
=840m2
学以致用
5.
思路分析:
①算出三角形的高
=60×2÷15
=8(m)
h=2S÷a
②算出梯形的面积
S=(a+b)×h÷2
=(5+15)×8÷2
=20×8÷2
=20×4
=80m2
课堂小结
●这节课我学会了用( )方法
推导梯形的面积,在前面我还用这种方法推导出了( )和( )的面积。
●两个( )的梯形可以拼成一个平行四边形。这个平行四边形的底等于梯形的( )与( )的和,高等于梯形的( ),每个梯形的面积等于拼成的平行四边形面积的( )。
梯形面积用字母表示为( )。
完全一样
上底
下底
高
一半
S=(a+b)×h÷2
转化的
平行四边形
三角形
思维练习
在下图的梯形中,剪下一个最大的三角形,剩下的是什么图形?剩下的图形的面积是多少平方厘米?
25厘米
10厘米
15厘米
s=ah÷2
=15×10÷2
=15×5
=75(cm2)
