北师大版数学八年级下册 5.2 分式的乘除法 课件 (共37张PPT)
文档属性
| 名称 | 北师大版数学八年级下册 5.2 分式的乘除法 课件 (共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 474.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 10:51:54 | ||
图片预览











文档简介
(共37张PPT)
5.2 分式的乘除法
北师大版 八年级 数学 下册
1.一个长方体容器的容积为V,底面的长为a,宽为b,当容器内的水占容积的 时,水高多少
长方体容器的高为 ,
水高为
解:
导入新知
2.大拖拉机m天耕地a公顷,小拖拉机n天耕地b公顷,大拖拉机的工作效率是小拖拉机的工作效率的多少倍
大拖拉机的工作效率是 公顷/天,小拖拉机的工作效率是 公顷/天,大拖拉机的工作效率是小拖拉机的工作效率的( )倍.
解:
导入新知
1. 掌握分式的乘除运算法则.
2. 能够进行分子、分母为多项式的分式乘除法运算.
素养目标
3. 能解决一些与分式乘除运算有关的简单的实际问题.
想一想:
类比分数的乘除法法则,你能说出分式的乘除法法则吗?
1.填空:
探究新知
知识点 1
分式的乘除
类似于分数,分式有:
乘法法则:
两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母.
除法法则:
两个分式相乘,把除式的分子和分母颠倒位置后再与被除式相乘.
上述法则用式子表示为:
结论
探究新知
对于 ,小明是这样计算的:
他的计算过程正确吗?为什么?
乘除属于同级运算,应按从左向右的顺序计算.
想一想:
探究新知
1.分式的分子、分母都是几个因式的积的形式,可先约去分子、分母的公因式,再按照法则进行计算.
2.分子或分母是多项式的按以下方法进行:
①将原分式中含同一字母的各多项式按降幂(或升幂)排列;在乘除过程中遇到整式则视其为分母为1,分子为这个整式的分式;
②把各分式中分子或分母里的多项式分解因式;
③应用分式乘除法法则进行运算;(注意:结果为最简分式或整式.)
分式乘除法的解题步骤
结论
探究新知
计算:
在分式的运算中,结果通常要化成最简分式或整式.
解:
分式的乘除
素养考点 1
探究新知
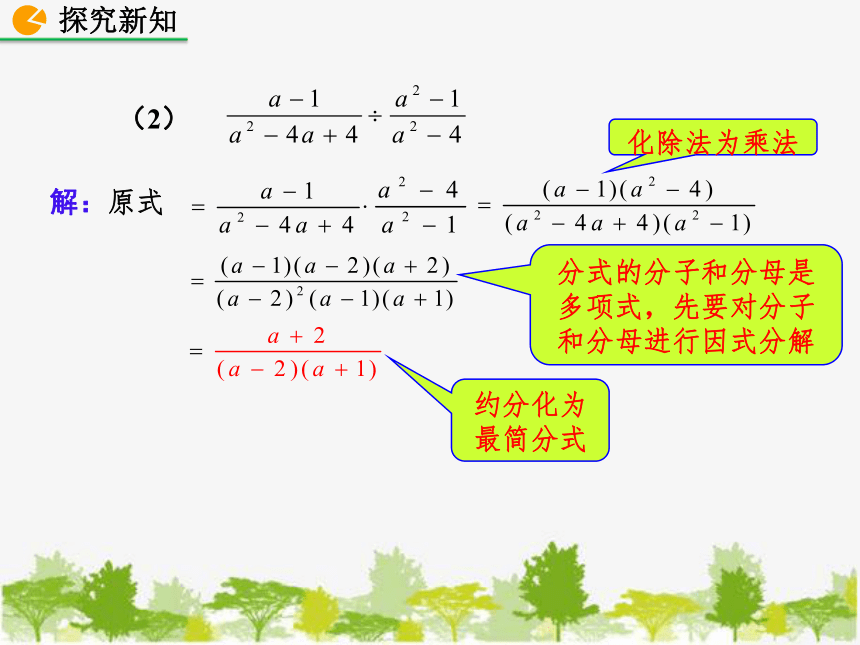
例1
(1)
(2)
计算:
例2
解:原式
探究新知
(1)
注意1:
分子和分母都是单项式的分式乘除法的解题步骤:
①把分式除法运算变成分式乘法运算;
②求分式的积;
③确定积的符号;
④约分.
探究新知
化除法为乘法
分式的分子和分母是多项式,先要对分子和分母进行因式分解
约分化为
最简分式
解:原式
探究新知
(2)
注意2:
分子或分母是多项式的分式乘除法的解题步骤是:
①除法转化为乘法;
②把各分式中分子或分母里的多项式分解因式;
③约去分子与分母的公因式.
探究新知
计算:
解:
巩固练习
变式训练
(1)
(2)
(1)
解:原式
巩固练习
变式训练
;
;
(2)
解:原式
巩固练习
.
.
1.根据乘方的意义计算下列各式:
探究新知
知识点 2
分式的乘方
2.类比分数的乘方运算,你能计算下列各式吗?
10个
探究新知
想一想:
一般地,当n是正整数时,
n个
n个
n个
这就是说,分式乘方要把分子、分母分别乘方.
探究新知
乘方符号法则:奇负偶正
探究新知
目前为止,正整数指数幂的运算法则都有什么?
(1) am·an =am+n ;
(2) am÷an=am-n;
(3) (am)n=amn;
(4) (ab)n=anbn;
想一想:
探究新知
(5)
分式的乘方法则
理解要点:
(1)分式乘方时,一定要把分子、分母分别乘方,不要把 写成 .
(2)分式乘方时,要首先确定乘方结果的符号,负数的偶次方为正,负数的奇次方为负.
(3)含有乘方的分式乘除混合运算,先算分式的乘方,再算乘除.
×
√
结论
探究新知
例1 化简:
解:原式=
含乘方的分式乘除混合运算
探究新知
素养考点 1
下列运算中正确的是 ( )
D
巩固练习
变式训练
分式的乘除法应用
素养考点 2
探究新知
做一做:
购买西瓜时, 人们总是希望西瓜瓤占整个西瓜的比例越大越好.假如我们把西瓜都看成球形,并且西瓜瓤的分布是均匀的,西瓜的皮厚都是d,已知球的体积公式为 (其中R为球的半径),那么
(1)西瓜瓤与整个西瓜的体积各是多少
(2)西瓜瓤与整个西瓜的体积的比是多少
(3)你认为买大西瓜合算还是买小西瓜合算 与同伴交流.
解:(1)西瓜瓤的体积:
整个西瓜的体积:
(2)
(3)买大西瓜合算.
探究新知
一条船往返于水路相距100 km的A,B两地之间,已知水流的速度是每小时2 km,船在静水中的速度是每小时x km(x>2),那么船在往返一次过程中,顺流航行的时间与逆流航行的时间比是______.
解析:顺流速度为(x+2)km/h,逆流速度为
(x-2)km/h,由题意得
巩固练习
变式训练
.
连接中考
(2020·随州) 的计算结果为( )
A. B. C. D.
B
1.化简 的结果是( )
A. B. x-1
C. x+1 D. x
C
课堂检测
基础巩固题
2.计算 等于( )
A. B. C. D.
C
3.计算:
解:原式=
课堂检测
原式=
基础巩固题
4.化简:
解:
课堂检测
基础巩固题
5.先化简,再求值: 其中a=2 019.
解:原式=
=(a-1)· =a+1,
当a=2 019时,原式=2 020.
课堂检测
基础巩固题
1.(1)已知x=-1,求(x-2)÷ 的值.
(2)已知a=5,求 的值.
课堂检测
解:(1)当x=-1时,
原式=(x-2)· =-(x+2)=-1.
(2)当a=5时,原式= ·(a-3)· =8.
能力提升题
2.已知(x2+2x+2)(x+3y)=0(y≠0),
求 ·(x-y)的值.
解:∵(x2+2x+2)(x+3y)=0, x2+2x+2=(x+1)2+1>0,
∴x+3y=0,即x=-3y,
原式=
课堂检测
能力提升题
课堂上,老师给大家出了这样一道题,“当x分别取3,- ,7+ 时,求分式 的值,”小明一看,“太复杂了,怎么算呢 ”你能帮小明解决这个问题吗 请你写出具体的解题过程.
解:原式=
所以分式的值与x的取值无关,
故不需要将x的值代入计算,直接化简分式即可.
课堂检测
拓广探索题
分式乘除运算
乘除法运算
注意
(1)分子分母是单项式的,先按法则进行,再约分化成最简分式或整式
除法先转化成乘法,再按照乘法法则进行运算
(2)分子分母是多项式的,通常要先分解因式再按法则进行
(3)运用法则时要注意符号的变化
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
5.2 分式的乘除法
北师大版 八年级 数学 下册
1.一个长方体容器的容积为V,底面的长为a,宽为b,当容器内的水占容积的 时,水高多少
长方体容器的高为 ,
水高为
解:
导入新知
2.大拖拉机m天耕地a公顷,小拖拉机n天耕地b公顷,大拖拉机的工作效率是小拖拉机的工作效率的多少倍
大拖拉机的工作效率是 公顷/天,小拖拉机的工作效率是 公顷/天,大拖拉机的工作效率是小拖拉机的工作效率的( )倍.
解:
导入新知
1. 掌握分式的乘除运算法则.
2. 能够进行分子、分母为多项式的分式乘除法运算.
素养目标
3. 能解决一些与分式乘除运算有关的简单的实际问题.
想一想:
类比分数的乘除法法则,你能说出分式的乘除法法则吗?
1.填空:
探究新知
知识点 1
分式的乘除
类似于分数,分式有:
乘法法则:
两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母.
除法法则:
两个分式相乘,把除式的分子和分母颠倒位置后再与被除式相乘.
上述法则用式子表示为:
结论
探究新知
对于 ,小明是这样计算的:
他的计算过程正确吗?为什么?
乘除属于同级运算,应按从左向右的顺序计算.
想一想:
探究新知
1.分式的分子、分母都是几个因式的积的形式,可先约去分子、分母的公因式,再按照法则进行计算.
2.分子或分母是多项式的按以下方法进行:
①将原分式中含同一字母的各多项式按降幂(或升幂)排列;在乘除过程中遇到整式则视其为分母为1,分子为这个整式的分式;
②把各分式中分子或分母里的多项式分解因式;
③应用分式乘除法法则进行运算;(注意:结果为最简分式或整式.)
分式乘除法的解题步骤
结论
探究新知
计算:
在分式的运算中,结果通常要化成最简分式或整式.
解:
分式的乘除
素养考点 1
探究新知
例1
(1)
(2)
计算:
例2
解:原式
探究新知
(1)
注意1:
分子和分母都是单项式的分式乘除法的解题步骤:
①把分式除法运算变成分式乘法运算;
②求分式的积;
③确定积的符号;
④约分.
探究新知
化除法为乘法
分式的分子和分母是多项式,先要对分子和分母进行因式分解
约分化为
最简分式
解:原式
探究新知
(2)
注意2:
分子或分母是多项式的分式乘除法的解题步骤是:
①除法转化为乘法;
②把各分式中分子或分母里的多项式分解因式;
③约去分子与分母的公因式.
探究新知
计算:
解:
巩固练习
变式训练
(1)
(2)
(1)
解:原式
巩固练习
变式训练
;
;
(2)
解:原式
巩固练习
.
.
1.根据乘方的意义计算下列各式:
探究新知
知识点 2
分式的乘方
2.类比分数的乘方运算,你能计算下列各式吗?
10个
探究新知
想一想:
一般地,当n是正整数时,
n个
n个
n个
这就是说,分式乘方要把分子、分母分别乘方.
探究新知
乘方符号法则:奇负偶正
探究新知
目前为止,正整数指数幂的运算法则都有什么?
(1) am·an =am+n ;
(2) am÷an=am-n;
(3) (am)n=amn;
(4) (ab)n=anbn;
想一想:
探究新知
(5)
分式的乘方法则
理解要点:
(1)分式乘方时,一定要把分子、分母分别乘方,不要把 写成 .
(2)分式乘方时,要首先确定乘方结果的符号,负数的偶次方为正,负数的奇次方为负.
(3)含有乘方的分式乘除混合运算,先算分式的乘方,再算乘除.
×
√
结论
探究新知
例1 化简:
解:原式=
含乘方的分式乘除混合运算
探究新知
素养考点 1
下列运算中正确的是 ( )
D
巩固练习
变式训练
分式的乘除法应用
素养考点 2
探究新知
做一做:
购买西瓜时, 人们总是希望西瓜瓤占整个西瓜的比例越大越好.假如我们把西瓜都看成球形,并且西瓜瓤的分布是均匀的,西瓜的皮厚都是d,已知球的体积公式为 (其中R为球的半径),那么
(1)西瓜瓤与整个西瓜的体积各是多少
(2)西瓜瓤与整个西瓜的体积的比是多少
(3)你认为买大西瓜合算还是买小西瓜合算 与同伴交流.
解:(1)西瓜瓤的体积:
整个西瓜的体积:
(2)
(3)买大西瓜合算.
探究新知
一条船往返于水路相距100 km的A,B两地之间,已知水流的速度是每小时2 km,船在静水中的速度是每小时x km(x>2),那么船在往返一次过程中,顺流航行的时间与逆流航行的时间比是______.
解析:顺流速度为(x+2)km/h,逆流速度为
(x-2)km/h,由题意得
巩固练习
变式训练
.
连接中考
(2020·随州) 的计算结果为( )
A. B. C. D.
B
1.化简 的结果是( )
A. B. x-1
C. x+1 D. x
C
课堂检测
基础巩固题
2.计算 等于( )
A. B. C. D.
C
3.计算:
解:原式=
课堂检测
原式=
基础巩固题
4.化简:
解:
课堂检测
基础巩固题
5.先化简,再求值: 其中a=2 019.
解:原式=
=(a-1)· =a+1,
当a=2 019时,原式=2 020.
课堂检测
基础巩固题
1.(1)已知x=-1,求(x-2)÷ 的值.
(2)已知a=5,求 的值.
课堂检测
解:(1)当x=-1时,
原式=(x-2)· =-(x+2)=-1.
(2)当a=5时,原式= ·(a-3)· =8.
能力提升题
2.已知(x2+2x+2)(x+3y)=0(y≠0),
求 ·(x-y)的值.
解:∵(x2+2x+2)(x+3y)=0, x2+2x+2=(x+1)2+1>0,
∴x+3y=0,即x=-3y,
原式=
课堂检测
能力提升题
课堂上,老师给大家出了这样一道题,“当x分别取3,- ,7+ 时,求分式 的值,”小明一看,“太复杂了,怎么算呢 ”你能帮小明解决这个问题吗 请你写出具体的解题过程.
解:原式=
所以分式的值与x的取值无关,
故不需要将x的值代入计算,直接化简分式即可.
课堂检测
拓广探索题
分式乘除运算
乘除法运算
注意
(1)分子分母是单项式的,先按法则进行,再约分化成最简分式或整式
除法先转化成乘法,再按照乘法法则进行运算
(2)分子分母是多项式的,通常要先分解因式再按法则进行
(3)运用法则时要注意符号的变化
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
