2021-2022学年人教版八年级数学下册18.2.1矩形的判定基础练习二(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.2.1矩形的判定基础练习二(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 147.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-26 23:56:35 | ||
图片预览



文档简介
18.2.1矩形的判定基础练习一
一、选择题
如下图,在中,,点E,点F分别是AC,BC的中点,D是斜边AB上一点,添加下列条件可以使四边形DECF成为矩形的是
A. B.
C. D.
如下图,在RtABC中,ACB=,点E,点F分别是AC,BC的中点,D是斜边AB上一点,添加下列条件可以使四边形DECF成为矩形的是( )
A. B.
C. D.
如图,Rt△ABC和Rt△CDE中,∠A=30°,∠E=45°,AB=CE,∠BCD=30°,FG⊥AB,下列结论:①CH=FH;②BC=GC;③四边形BDEF为平行四边形;④FH=GF+BH.其中正确的结论是()
A. B. C. D.
下列条件中,不能判定 ABCD为矩形的是( )
A. B. C. D.
二、填空题
如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 .
阅读下面材料:在数学课上,老师提出如下问题:
已知:Rt△ABC,∠ABC=90°.
求作:矩形ABCD.
小敏的作法如下:
①作线段AC的垂直平分线交AC于点O;
②连接BO并延长,在延长线上截取OD=BO;
③连接DA,DC.
则四边形ABCD即为所求.
老师说:“小敏的作法正确.”
请回答:小敏的作图依据是_____________________________________________________________________________________.
在四边形ABCD中,对角线AC,BD交于点O,且AC,BD互相平分,若添加一个条件使得四边形ABCD是矩形,则这个条件可以是 (填写一个即可).
如图,在四边形ABCD中,∠C=∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是 (写出一种情况即可).
用一把刻度尺来判定一个四边形零件是矩形的方法是先测量两组对边是否相等,然后测量两条对角线是否相等,这样做的依据是______________.
三、解答题
如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:AC=BE;
(2)若∠AFC=2∠D,连接AC,BE.求证:四边形ABEC是矩形.
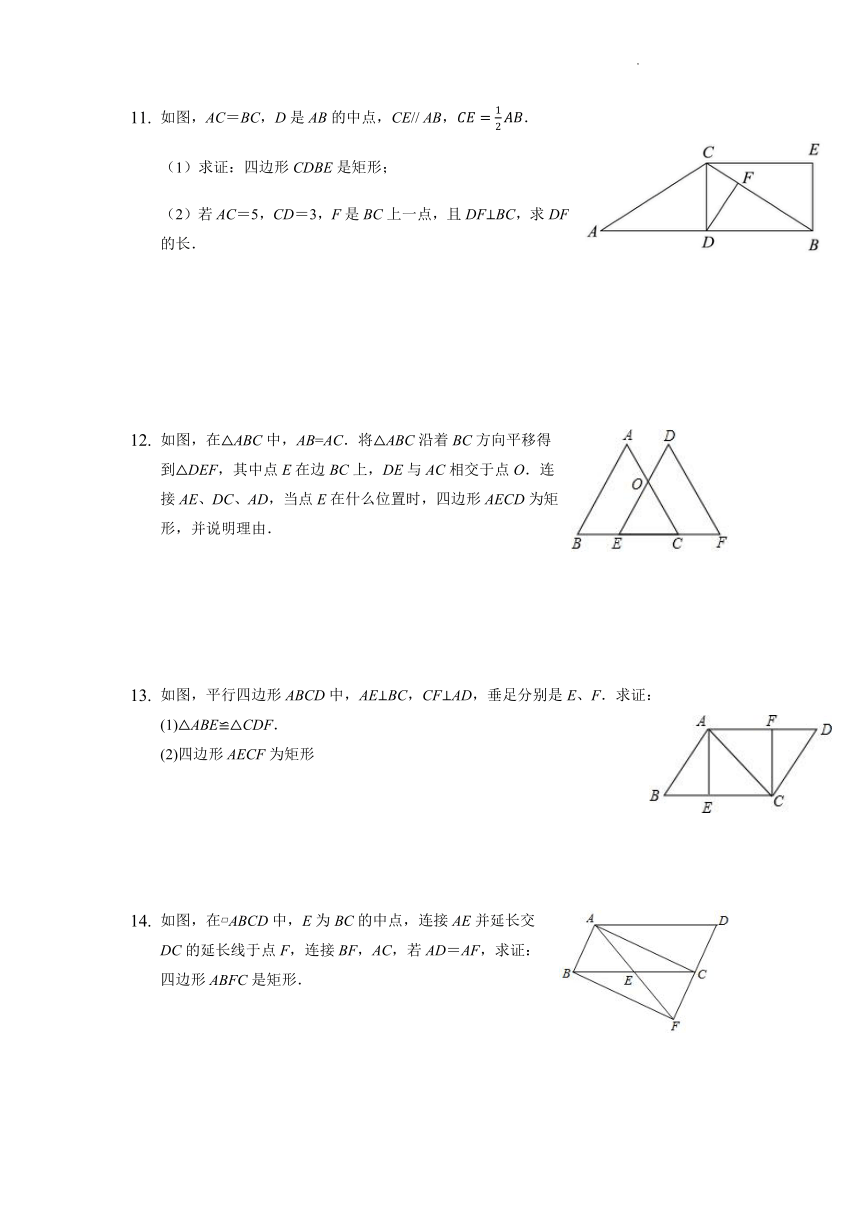
如图,AC=BC,D是AB的中点,CE// AB,.
(1)求证:四边形CDBE是矩形;
(2)若AC=5,CD=3,F是BC上一点,且DF⊥BC,求DF的长.
如图,在△ABC中,AB=AC.将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.连接AE、DC、AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.
如图,平行四边形ABCD中,AE⊥BC,CF⊥AD,垂足分别是E、F.求证:
(1)△ABE≌△CDF.
(2)四边形AECF为矩形
如图,在 ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,求证:四边形ABFC是矩形.
如图,在ABC中,O是边AC上的一个动点,过点O作直线MNBC,交ACB的平分线于点E,交ABC的外角ACD的平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)连接AE,AF,当点O在边AC上运动到什么位置时,四边形AECF是矩形 请说明理由.
参考答案
1.【答案】A
2.【答案】A
3.【答案】B
4.【答案】A
5.【答案】12
6.【答案】对角线互相平分的四边形是平行四边形,有一个角是直角的平行四边形是矩形
7.【答案】 AC=BD或有个内角等于90度(填一个即可)
8.【答案】∠A=90°(答案不唯一)
9.【答案】对角线相等的平行四边形是矩形
10.【答案】证明:(1)∵四边形ABCD是平行四边形,
∴AB // CD,AB=CD.
∵CE=DC,
∴AB=EC,AB // EC,
∴四边形ABEC是平行四边形,
∴AC=BE.
(2)∵四边形ABEC是平行四边形,
∴FA=FE,FB=FC.
∵四边形ABCD是平行四边形,
∴∠ABC=∠D.
又∵∠AFC=2∠D,
∴∠AFC=2∠ABC.
∵∠AFC=∠ABC+∠BAF,
∴∠ABC=∠BAF,
∴FA=FB,
∴FA=FE=FB=FC,
∴AE=BC,
∴四边形ABEC是矩形.
11.【答案】(1)证明:因为AC=BC,
所以△ACB是等腰三角形.
因为D是AB中点,
所以,CD⊥DB.
因为,
所以DB=CE.
因为CE // AB,
所以四边形CDBE是平行四边形.
又因为CD⊥DB,
所以四边形CDBE是矩形;
(2)解:在Rt△CDB中,∠CDB=90°,CB=AC=5,CD=3,
所以.
因为DF⊥BC于F,
所以,
×5 DF=×3×4,
解得.
12.【答案】解:当E为BC的中点时,四边形AECD是矩形,理由如下:
如图所示:
∵AB=AC,E为BC的中点,
∴AE⊥BC,BE=EC,
∵△ABC平移得到△DEF,
∴BE∥AD,BE=AD,
∴AD∥EC,AD=EC,
∴四边形AECD是平行四边形,
∵AE⊥BC,
∴四边形AECD是矩形.
13.【答案】证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D,
∵AE⊥BC,CF⊥AD,
∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF(AAS);
(2)∵△ABE≌△CDF,
∴BE=DF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AF∥CE,AF=CE,
∴四边形AECF是平行四边形,
∵AE⊥BC,
∴∠AEC=90°,
∴四边形AECF是矩形.
14.【答案】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
∵E为BC的中点,
∴EB=EC,
∴△ABE≌△FCE(AAS),
∴AB=CF.
∵AB∥CF,
∴四边形ABFC是平行四边形,
在 ABCD中,AD=BC,
又∵AD=AF,
∴BC=AF,
∴四边形ABFC是矩形.
15.【答案】(1)证明:如图所示,
∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)解:∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=12,CF=5,
∴EF==13,
∴OC=EF=6.5;
(3)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
理由如下:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
第2页,共2页
一、选择题
如下图,在中,,点E,点F分别是AC,BC的中点,D是斜边AB上一点,添加下列条件可以使四边形DECF成为矩形的是
A. B.
C. D.
如下图,在RtABC中,ACB=,点E,点F分别是AC,BC的中点,D是斜边AB上一点,添加下列条件可以使四边形DECF成为矩形的是( )
A. B.
C. D.
如图,Rt△ABC和Rt△CDE中,∠A=30°,∠E=45°,AB=CE,∠BCD=30°,FG⊥AB,下列结论:①CH=FH;②BC=GC;③四边形BDEF为平行四边形;④FH=GF+BH.其中正确的结论是()
A. B. C. D.
下列条件中,不能判定 ABCD为矩形的是( )
A. B. C. D.
二、填空题
如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 .
阅读下面材料:在数学课上,老师提出如下问题:
已知:Rt△ABC,∠ABC=90°.
求作:矩形ABCD.
小敏的作法如下:
①作线段AC的垂直平分线交AC于点O;
②连接BO并延长,在延长线上截取OD=BO;
③连接DA,DC.
则四边形ABCD即为所求.
老师说:“小敏的作法正确.”
请回答:小敏的作图依据是_____________________________________________________________________________________.
在四边形ABCD中,对角线AC,BD交于点O,且AC,BD互相平分,若添加一个条件使得四边形ABCD是矩形,则这个条件可以是 (填写一个即可).
如图,在四边形ABCD中,∠C=∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是 (写出一种情况即可).
用一把刻度尺来判定一个四边形零件是矩形的方法是先测量两组对边是否相等,然后测量两条对角线是否相等,这样做的依据是______________.
三、解答题
如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:AC=BE;
(2)若∠AFC=2∠D,连接AC,BE.求证:四边形ABEC是矩形.
如图,AC=BC,D是AB的中点,CE// AB,.
(1)求证:四边形CDBE是矩形;
(2)若AC=5,CD=3,F是BC上一点,且DF⊥BC,求DF的长.
如图,在△ABC中,AB=AC.将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.连接AE、DC、AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.
如图,平行四边形ABCD中,AE⊥BC,CF⊥AD,垂足分别是E、F.求证:
(1)△ABE≌△CDF.
(2)四边形AECF为矩形
如图,在 ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,求证:四边形ABFC是矩形.
如图,在ABC中,O是边AC上的一个动点,过点O作直线MNBC,交ACB的平分线于点E,交ABC的外角ACD的平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)连接AE,AF,当点O在边AC上运动到什么位置时,四边形AECF是矩形 请说明理由.
参考答案
1.【答案】A
2.【答案】A
3.【答案】B
4.【答案】A
5.【答案】12
6.【答案】对角线互相平分的四边形是平行四边形,有一个角是直角的平行四边形是矩形
7.【答案】 AC=BD或有个内角等于90度(填一个即可)
8.【答案】∠A=90°(答案不唯一)
9.【答案】对角线相等的平行四边形是矩形
10.【答案】证明:(1)∵四边形ABCD是平行四边形,
∴AB // CD,AB=CD.
∵CE=DC,
∴AB=EC,AB // EC,
∴四边形ABEC是平行四边形,
∴AC=BE.
(2)∵四边形ABEC是平行四边形,
∴FA=FE,FB=FC.
∵四边形ABCD是平行四边形,
∴∠ABC=∠D.
又∵∠AFC=2∠D,
∴∠AFC=2∠ABC.
∵∠AFC=∠ABC+∠BAF,
∴∠ABC=∠BAF,
∴FA=FB,
∴FA=FE=FB=FC,
∴AE=BC,
∴四边形ABEC是矩形.
11.【答案】(1)证明:因为AC=BC,
所以△ACB是等腰三角形.
因为D是AB中点,
所以,CD⊥DB.
因为,
所以DB=CE.
因为CE // AB,
所以四边形CDBE是平行四边形.
又因为CD⊥DB,
所以四边形CDBE是矩形;
(2)解:在Rt△CDB中,∠CDB=90°,CB=AC=5,CD=3,
所以.
因为DF⊥BC于F,
所以,
×5 DF=×3×4,
解得.
12.【答案】解:当E为BC的中点时,四边形AECD是矩形,理由如下:
如图所示:
∵AB=AC,E为BC的中点,
∴AE⊥BC,BE=EC,
∵△ABC平移得到△DEF,
∴BE∥AD,BE=AD,
∴AD∥EC,AD=EC,
∴四边形AECD是平行四边形,
∵AE⊥BC,
∴四边形AECD是矩形.
13.【答案】证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D,
∵AE⊥BC,CF⊥AD,
∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF(AAS);
(2)∵△ABE≌△CDF,
∴BE=DF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AF∥CE,AF=CE,
∴四边形AECF是平行四边形,
∵AE⊥BC,
∴∠AEC=90°,
∴四边形AECF是矩形.
14.【答案】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
∵E为BC的中点,
∴EB=EC,
∴△ABE≌△FCE(AAS),
∴AB=CF.
∵AB∥CF,
∴四边形ABFC是平行四边形,
在 ABCD中,AD=BC,
又∵AD=AF,
∴BC=AF,
∴四边形ABFC是矩形.
15.【答案】(1)证明:如图所示,
∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)解:∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=12,CF=5,
∴EF==13,
∴OC=EF=6.5;
(3)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
理由如下:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
第2页,共2页
