青岛版八年级数学上册 第3章 分式 复习课件(共26张PPT)
文档属性
| 名称 | 青岛版八年级数学上册 第3章 分式 复习课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 817.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 11:07:04 | ||
图片预览








文档简介
(共26张PPT)
分 式
复习课
01
知识构架
03
典型例题
02
复习回顾
04
随堂练习
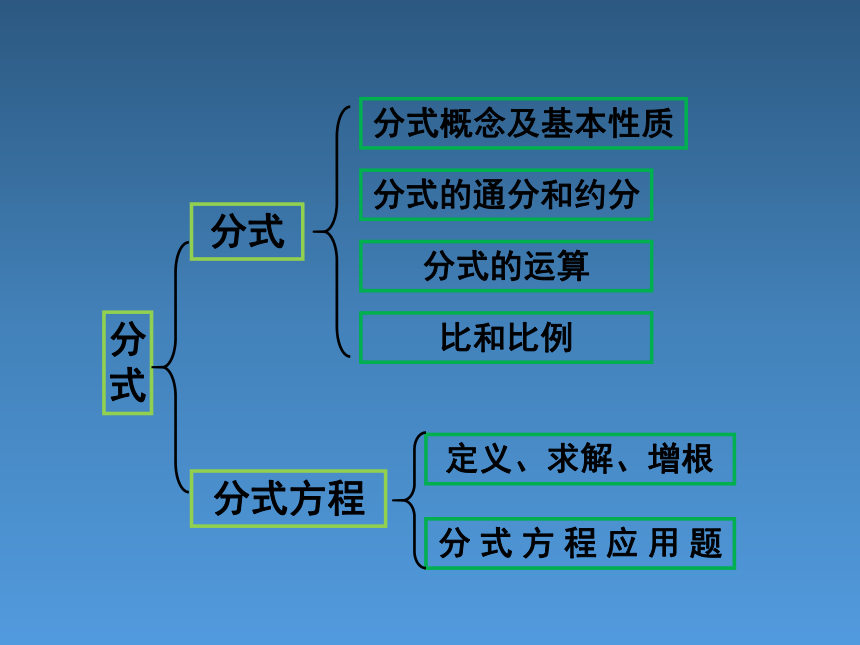
分式
分式
分式方程
定义、求解、增根
分 式 方 程 应 用 题
分式概念及基本性质
分式的通分和约分
分式的运算
比和比例
1.分式概念
其中,A叫做分式的分子,B叫做分式的分母。
如果把除法算式A÷B写成 的形式,其中A、B都是整式, 且B中含有字母,那么称代数式 为分式(fraction).
分式有无意义及值为0
在分式中,分母的值不能是零。分式中的分母如果是零,则分式没有意义。
因为零不能作为除数,所以分数的分母不能是零。
在分式中,当分子为零而分母不为零时,分式的值为零。
分式的分子与分母都乘(或除以)同一个不等于零的整式,分式的值不变,用等式表示是:
或
(其中M是不等于零的整式)
2.基本性质
3.运算法则
两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母;
两个分式相除,把除式的分子分母颠倒位置后,再与被除式相乘.
分式乘除运算法则
分式的乘方,把分子、分母分别乘方。即
分式乘方运算法则
同分母的分式相加减,分母不变,分子相加减.
分式加减运算法则
异分母的分式相加减,先把他们通分,变成同分母分式,再加减.
约分、最简分式
4.通分和约分
约分:
利用分式的基本性质,把一个分式的分子和分母中1以外的公因式约去,叫做约分.
最简分式:
当一个分式的分子和分母中1以外没有其他的公因式时,这样的分式叫做最简分式.
最简公分母:
各分母中系数的最小公倍数与所有字母因式的最高次幂的乘积.
最简公分母、通分
通分:
把几个异分母的分式化成与原来的分式相等的同分母分式的变形叫做通分.
如果分母是多项式,首先要进行因式分解.
4.比和比例
两个数a与b(b≠0)相除,叫做a与b的比。
其中,a叫做比的前项,b叫做比的后项。
表示两个比相等的式子叫做比例式,简称比例.
注:当比例的两个内项相等,即当
时,b叫做a和c的比例中项.
在比例中,两外项的乘积等于两内项的乘积.
比例的基本性质
分母中含有未知数的方程叫做分式方程.
5.分式方程
解分式方程的步骤:
1.去分母,化为整式方程
2.解整式方程
3.验根
关键:找最简公分母
依据:等式的基本性质(2)
6.列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有三次检验.
6.答:注意单位和语言完整.且答案要生活化.
(1)当a=1,2时,分别求分式 的值。
(2)当a取何值时,分式 无意义?
(4)当a取何值时,分式 值为零?
(3)当a取何值时,分式 有意义?
例1.下列分式何时有意义、无意义、值为0?
例2.计算下列各题:
例3.解方程:
例4.应用题
(1)农机厂职工到距工厂15千米的某地去检修农机,一部分人骑自车走,过了40分钟,其余的人乘汽车出发,他们同时到达,已知汽车的速度是自行车速度的3倍,求两种车的速度。
(2)甲、乙两人骑自行车各行28公里,甲比乙快0.25小时,已知甲与乙速度比为8:7,求两人速度。
解:设甲的速度8x千米/时,乙的速度是7x千米/时。
(3)某学校要做一批校服,已知甲做5件与乙做6件所用的时间相同,且两人每天共做55件,求甲、乙两人每天各做多少件?
(4)一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,问规定日期是几天?
1.当x=200时,求 的值。
2.若关于x的方程 有增根,则 k的值是多少?
3.一船在静水中每小时航行20千米,顺水航行72千米的时间恰好等于逆水航行48千米的时间,求每小时的水流速度。
4.把总价都为480元的甲、乙两种糖果混合成杂拌糖,杂拌糖平均价每块比甲种糖少0.03元,比乙种糖多0.02元,则原来甲种糖和乙种糖的价格各是多少元?甲、乙两种糖各有多少块?
分 式
复习课
01
知识构架
03
典型例题
02
复习回顾
04
随堂练习
分式
分式
分式方程
定义、求解、增根
分 式 方 程 应 用 题
分式概念及基本性质
分式的通分和约分
分式的运算
比和比例
1.分式概念
其中,A叫做分式的分子,B叫做分式的分母。
如果把除法算式A÷B写成 的形式,其中A、B都是整式, 且B中含有字母,那么称代数式 为分式(fraction).
分式有无意义及值为0
在分式中,分母的值不能是零。分式中的分母如果是零,则分式没有意义。
因为零不能作为除数,所以分数的分母不能是零。
在分式中,当分子为零而分母不为零时,分式的值为零。
分式的分子与分母都乘(或除以)同一个不等于零的整式,分式的值不变,用等式表示是:
或
(其中M是不等于零的整式)
2.基本性质
3.运算法则
两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母;
两个分式相除,把除式的分子分母颠倒位置后,再与被除式相乘.
分式乘除运算法则
分式的乘方,把分子、分母分别乘方。即
分式乘方运算法则
同分母的分式相加减,分母不变,分子相加减.
分式加减运算法则
异分母的分式相加减,先把他们通分,变成同分母分式,再加减.
约分、最简分式
4.通分和约分
约分:
利用分式的基本性质,把一个分式的分子和分母中1以外的公因式约去,叫做约分.
最简分式:
当一个分式的分子和分母中1以外没有其他的公因式时,这样的分式叫做最简分式.
最简公分母:
各分母中系数的最小公倍数与所有字母因式的最高次幂的乘积.
最简公分母、通分
通分:
把几个异分母的分式化成与原来的分式相等的同分母分式的变形叫做通分.
如果分母是多项式,首先要进行因式分解.
4.比和比例
两个数a与b(b≠0)相除,叫做a与b的比。
其中,a叫做比的前项,b叫做比的后项。
表示两个比相等的式子叫做比例式,简称比例.
注:当比例的两个内项相等,即当
时,b叫做a和c的比例中项.
在比例中,两外项的乘积等于两内项的乘积.
比例的基本性质
分母中含有未知数的方程叫做分式方程.
5.分式方程
解分式方程的步骤:
1.去分母,化为整式方程
2.解整式方程
3.验根
关键:找最简公分母
依据:等式的基本性质(2)
6.列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有三次检验.
6.答:注意单位和语言完整.且答案要生活化.
(1)当a=1,2时,分别求分式 的值。
(2)当a取何值时,分式 无意义?
(4)当a取何值时,分式 值为零?
(3)当a取何值时,分式 有意义?
例1.下列分式何时有意义、无意义、值为0?
例2.计算下列各题:
例3.解方程:
例4.应用题
(1)农机厂职工到距工厂15千米的某地去检修农机,一部分人骑自车走,过了40分钟,其余的人乘汽车出发,他们同时到达,已知汽车的速度是自行车速度的3倍,求两种车的速度。
(2)甲、乙两人骑自行车各行28公里,甲比乙快0.25小时,已知甲与乙速度比为8:7,求两人速度。
解:设甲的速度8x千米/时,乙的速度是7x千米/时。
(3)某学校要做一批校服,已知甲做5件与乙做6件所用的时间相同,且两人每天共做55件,求甲、乙两人每天各做多少件?
(4)一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,问规定日期是几天?
1.当x=200时,求 的值。
2.若关于x的方程 有增根,则 k的值是多少?
3.一船在静水中每小时航行20千米,顺水航行72千米的时间恰好等于逆水航行48千米的时间,求每小时的水流速度。
4.把总价都为480元的甲、乙两种糖果混合成杂拌糖,杂拌糖平均价每块比甲种糖少0.03元,比乙种糖多0.02元,则原来甲种糖和乙种糖的价格各是多少元?甲、乙两种糖各有多少块?
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
