2020-2021学年人教版八年级下册数学第18章 平行四边形 单元测试(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学第18章 平行四边形 单元测试(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 190.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 10:40:19 | ||
图片预览




文档简介
《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
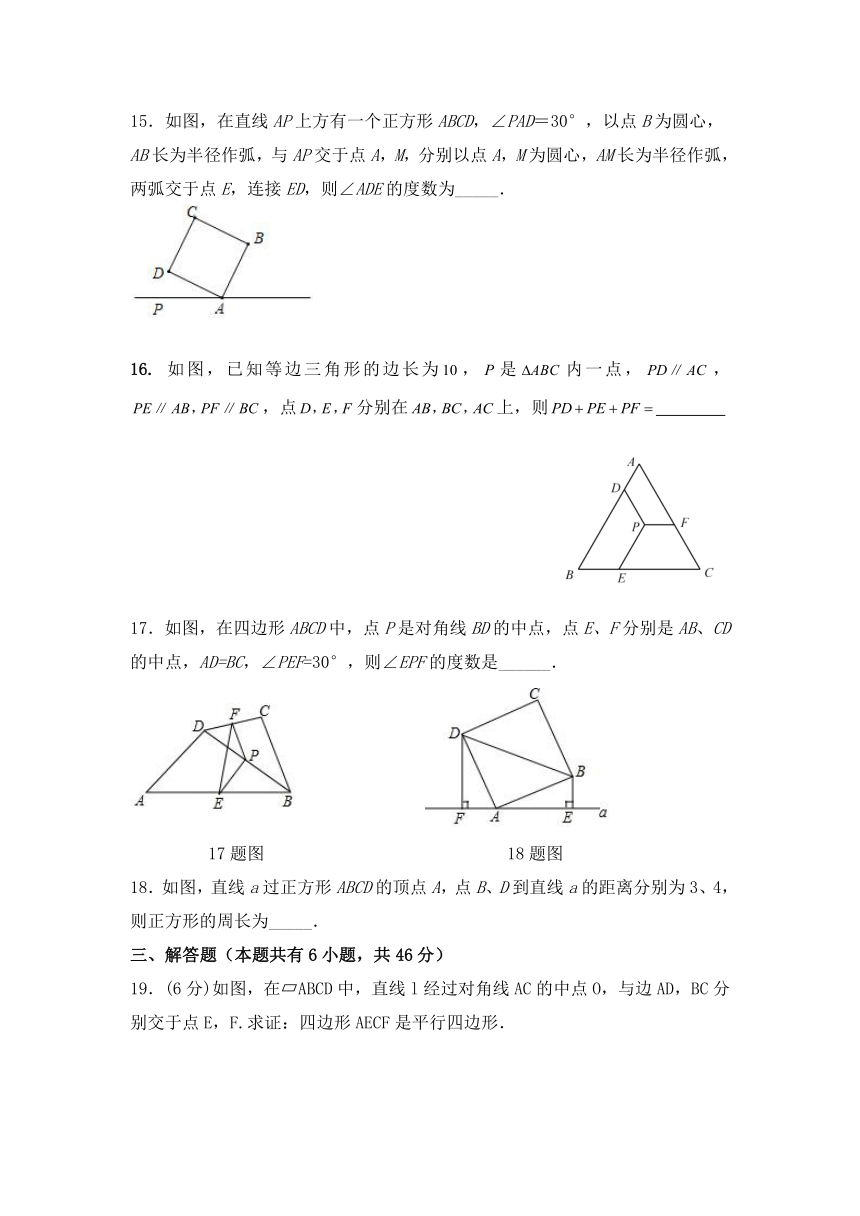
一.选择题(每题3分,共30分)
1.如图,△ABC中,AB=AC=12,BC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
A.11 B.17 C.18 D.16
2.下列性质中,菱形具有而矩形不一定具有的是( )
A.对角线相等 B.对角线垂直 C.邻边垂直 D.邻角互补
3.如图,矩形ABCD的对角线AC,BD相交于点O,且∠AOD=120°.过点A作AE⊥BD于点E,则BE:ED等于( )
A.1:3 B.1:4 C.2:3 D.2:5
4.如图,四边形ABCD中,以对角线AC为斜边作Rt△ACE,连接BE、DE,BE⊥DE,AC,BD互相平分.若2AB=BC=4,则BD的值为( )
A.2 B. C.3 D.4
5. 从等腰三角形底边上任一点分别作两腰的平行线,所成的平行四边形的周长等于这个等腰三角形的 ( )
A.周长 B.周长的一半 C.腰长 D.腰长的2倍
6.如图1,在平行四边形ABCD中,下列各式不一定正确的是 ( )
A. B.
C. D.
图1 图2
7.如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别是线段OA、OB的中点,若AC+BD=32cm,△OEF的周长为13cm,则CD的长为( )
A.12cm B.10cm C.8cm D.6cm
8.如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
A.矩形 B.菱形C.一般的四边形 D.平行四边形
9.如图,E,F分别是 ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( )
A.6 B.12 C.18 D.24
10.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
A.45° B.35° C.22.5° D.15.5°
二、填空题(每题3分,共30分)
11.如图所示,在 ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为 .
12.如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是 .
13.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 .
14.如图,已知菱形ABCD的周长为16,面积为8,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
15.如图,在直线AP上方有一个正方形ABCD,∠PAD=30°,以点B为圆心,AB长为半径作弧,与AP交于点A,M,分别以点A,M为圆心,AM长为半径作弧,两弧交于点E,连接ED,则∠ADE的度数为_____.
16. 如图,已知等边三角形的边长为,是内一点,,,点分别在上,则
17.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是______.
17题图 18题图
18.如图,直线a过正方形ABCD的顶点A,点B、D到直线a的距离分别为3、4,则正方形的周长为_____.
三、解答题(本题共有6小题,共46分)
19.(6分)如图,在 ABCD中,直线l经过对角线AC的中点O,与边AD,BC分别交于点E,F.求证:四边形AECF是平行四边形.
第19题图
20.(8分)如图,在平行四边形中挖去一个矩形,在请用无刻度的直尺,准确作出一条直线,将剩下图形的面积平分.(保留作图痕迹)
第20题图
21.(8分)如图,已知四边形ABCD为菱形,AE⊥BC于点E,AF⊥CD于点F.
(1)求证:AE=AF;
(2)若∠B=70°,求∠EAF的度数.
第21题图
22、(8分)如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.求证:(1)DM=BM;(2)MN⊥BD 。
23、(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)将△ABC沿水平方向向左平移3个单位得△A1B1C1,请画出△A1B1C1.
(2)作出△ABC关于O点成中心对称的△A2B2C2,并直接写出A2,B2,C2的坐标.
(3)△A1B1C1与△A2B2C2是否成中心对称,若是请写出对称中心的坐标 ,若不是请说明理由.
24.(8分)(1)尝试探究:
如图1,E是正方形ABCD的边AD上的一点,过点C作CF⊥CE,交AB的延长线于F.
①求证:△CDE≌△CBF;
②过点C作∠ECF的平分线交AB于P,连接PE,请探究PE与PF的数量关系,并证明你的结论.
(2)拓展应用:
如图2,E是正方形ABCD的边AD上的一点,过点C作CF⊥CE,交AB的延长线于F,连接EF交DB于M,连接CM并延长CM交AB于P,已知AB=6,DE=2,求PB的长.
参考答案
选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B A B D D D B C C
二.填空题
11.如图所示,在 ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为50°.
12.如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是24.
13.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为12.
14.如图,已知菱形ABCD的周长为16,面积为8,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为2.
15.15°或45°
16. 10
17,10、6;
18,4.
三、解答题
19.证明:∵四边形ABCD是平行四边形,∴AE∥FC,∴∠EAO=∠FCO.又∵∠AOE=∠COF,AO=CO,∴△AOE≌△COF(ASA),∴AE=FC,∴四边形AFCE是平行四边形.
20.第20题图
21.(1)∵菱形ABCD,∴AB=AD,∠B=∠D.又∵AE⊥BC于点E,AF⊥CD于点F,∴∠AEB=∠AFD=90°,∴△ABE≌△ADF,∴AE=AF. (2)∵∠D=∠B=70°,∠AEB=∠AFD=90°,∴∠BAE=∠DAF=20°,∵菱形ABCD,∴AD∥BC,∴∠BAD=110°,∴∠EAF=70°.
22、
23、解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求,A2(﹣1,﹣4),B2(﹣4,﹣2),C2(﹣3,﹣5);
(3)△A1B1C1与△A2B2C2成中心对称,对称中心的坐标为:(﹣1.5,0).
故答案为:(﹣1.5,0).
24.解:(1)如图1中,在正方形ABCD中,DC=BC,∠D=∠ABC=∠DCB=90°,
∴∠CBF=180°﹣∠ABC=90°,
∵CF⊥CE,
∴∠ECF=90°,
∴∠DCB=∠ECF=90°
∴∠DCE=∠BCF,
∴△CDE≌△CBF(ASA).
(2)结论:PE=PF.
理由:如图1中,∵△CDE≌△CBF,
∴CE=CF,
∵PC=PC,∠PCE=∠PCF,
∴△PCE≌△PCF(SAS),
∴PE=PF.
(3)如图2中,作EH⊥AD交BD于H,连接PE.
∵四边形ABCD是正方形,
∴AB=AD=6,∠A=90°,∠EDH=45°,
∵EH⊥AD,
∴∠DEH=∠A=90°,
∴EH∥AF,DE=EH=2,
∵△CDE≌△CBF,
∴DE=BF=2,
∴EH=BF,
∵∠EHM=∠MBF,∠EMH=∠FMB,
∴△EMH≌△FMB(AAS),
∵EM=FM,
∵CE=CF,
∴PC垂直平分线段EF,
∴PE=PF,设PB=x,则PE=PF=x+2,PA=6﹣x,
在Rt△APE中,则有(x+2)2=42+(6﹣x)2,
∴x=3,
∴PB=3.
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.如图,△ABC中,AB=AC=12,BC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
A.11 B.17 C.18 D.16
2.下列性质中,菱形具有而矩形不一定具有的是( )
A.对角线相等 B.对角线垂直 C.邻边垂直 D.邻角互补
3.如图,矩形ABCD的对角线AC,BD相交于点O,且∠AOD=120°.过点A作AE⊥BD于点E,则BE:ED等于( )
A.1:3 B.1:4 C.2:3 D.2:5
4.如图,四边形ABCD中,以对角线AC为斜边作Rt△ACE,连接BE、DE,BE⊥DE,AC,BD互相平分.若2AB=BC=4,则BD的值为( )
A.2 B. C.3 D.4
5. 从等腰三角形底边上任一点分别作两腰的平行线,所成的平行四边形的周长等于这个等腰三角形的 ( )
A.周长 B.周长的一半 C.腰长 D.腰长的2倍
6.如图1,在平行四边形ABCD中,下列各式不一定正确的是 ( )
A. B.
C. D.
图1 图2
7.如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别是线段OA、OB的中点,若AC+BD=32cm,△OEF的周长为13cm,则CD的长为( )
A.12cm B.10cm C.8cm D.6cm
8.如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
A.矩形 B.菱形C.一般的四边形 D.平行四边形
9.如图,E,F分别是 ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( )
A.6 B.12 C.18 D.24
10.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
A.45° B.35° C.22.5° D.15.5°
二、填空题(每题3分,共30分)
11.如图所示,在 ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为 .
12.如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是 .
13.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 .
14.如图,已知菱形ABCD的周长为16,面积为8,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
15.如图,在直线AP上方有一个正方形ABCD,∠PAD=30°,以点B为圆心,AB长为半径作弧,与AP交于点A,M,分别以点A,M为圆心,AM长为半径作弧,两弧交于点E,连接ED,则∠ADE的度数为_____.
16. 如图,已知等边三角形的边长为,是内一点,,,点分别在上,则
17.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是______.
17题图 18题图
18.如图,直线a过正方形ABCD的顶点A,点B、D到直线a的距离分别为3、4,则正方形的周长为_____.
三、解答题(本题共有6小题,共46分)
19.(6分)如图,在 ABCD中,直线l经过对角线AC的中点O,与边AD,BC分别交于点E,F.求证:四边形AECF是平行四边形.
第19题图
20.(8分)如图,在平行四边形中挖去一个矩形,在请用无刻度的直尺,准确作出一条直线,将剩下图形的面积平分.(保留作图痕迹)
第20题图
21.(8分)如图,已知四边形ABCD为菱形,AE⊥BC于点E,AF⊥CD于点F.
(1)求证:AE=AF;
(2)若∠B=70°,求∠EAF的度数.
第21题图
22、(8分)如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.求证:(1)DM=BM;(2)MN⊥BD 。
23、(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)将△ABC沿水平方向向左平移3个单位得△A1B1C1,请画出△A1B1C1.
(2)作出△ABC关于O点成中心对称的△A2B2C2,并直接写出A2,B2,C2的坐标.
(3)△A1B1C1与△A2B2C2是否成中心对称,若是请写出对称中心的坐标 ,若不是请说明理由.
24.(8分)(1)尝试探究:
如图1,E是正方形ABCD的边AD上的一点,过点C作CF⊥CE,交AB的延长线于F.
①求证:△CDE≌△CBF;
②过点C作∠ECF的平分线交AB于P,连接PE,请探究PE与PF的数量关系,并证明你的结论.
(2)拓展应用:
如图2,E是正方形ABCD的边AD上的一点,过点C作CF⊥CE,交AB的延长线于F,连接EF交DB于M,连接CM并延长CM交AB于P,已知AB=6,DE=2,求PB的长.
参考答案
选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B A B D D D B C C
二.填空题
11.如图所示,在 ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为50°.
12.如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是24.
13.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为12.
14.如图,已知菱形ABCD的周长为16,面积为8,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为2.
15.15°或45°
16. 10
17,10、6;
18,4.
三、解答题
19.证明:∵四边形ABCD是平行四边形,∴AE∥FC,∴∠EAO=∠FCO.又∵∠AOE=∠COF,AO=CO,∴△AOE≌△COF(ASA),∴AE=FC,∴四边形AFCE是平行四边形.
20.第20题图
21.(1)∵菱形ABCD,∴AB=AD,∠B=∠D.又∵AE⊥BC于点E,AF⊥CD于点F,∴∠AEB=∠AFD=90°,∴△ABE≌△ADF,∴AE=AF. (2)∵∠D=∠B=70°,∠AEB=∠AFD=90°,∴∠BAE=∠DAF=20°,∵菱形ABCD,∴AD∥BC,∴∠BAD=110°,∴∠EAF=70°.
22、
23、解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求,A2(﹣1,﹣4),B2(﹣4,﹣2),C2(﹣3,﹣5);
(3)△A1B1C1与△A2B2C2成中心对称,对称中心的坐标为:(﹣1.5,0).
故答案为:(﹣1.5,0).
24.解:(1)如图1中,在正方形ABCD中,DC=BC,∠D=∠ABC=∠DCB=90°,
∴∠CBF=180°﹣∠ABC=90°,
∵CF⊥CE,
∴∠ECF=90°,
∴∠DCB=∠ECF=90°
∴∠DCE=∠BCF,
∴△CDE≌△CBF(ASA).
(2)结论:PE=PF.
理由:如图1中,∵△CDE≌△CBF,
∴CE=CF,
∵PC=PC,∠PCE=∠PCF,
∴△PCE≌△PCF(SAS),
∴PE=PF.
(3)如图2中,作EH⊥AD交BD于H,连接PE.
∵四边形ABCD是正方形,
∴AB=AD=6,∠A=90°,∠EDH=45°,
∵EH⊥AD,
∴∠DEH=∠A=90°,
∴EH∥AF,DE=EH=2,
∵△CDE≌△CBF,
∴DE=BF=2,
∴EH=BF,
∵∠EHM=∠MBF,∠EMH=∠FMB,
∴△EMH≌△FMB(AAS),
∵EM=FM,
∵CE=CF,
∴PC垂直平分线段EF,
∴PE=PF,设PB=x,则PE=PF=x+2,PA=6﹣x,
在Rt△APE中,则有(x+2)2=42+(6﹣x)2,
∴x=3,
∴PB=3.
