人教版八年级数学下册20.2 数据的波动程度 同步练习(word版,含答案)
文档属性
| 名称 | 人教版八年级数学下册20.2 数据的波动程度 同步练习(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 78.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 23:17:31 | ||
图片预览


文档简介
初中数学·人教版·八年级下册——第二十章 数据的分析
20.2 数据的波动程度
测试时间:20分钟
一、选择题
1.2021年正值中国共产党建党100周年,某校开展“致敬建党百年,传承红色基因”党史知识竞赛活动.八年级甲、乙、丙、丁四个小组的同学分别参加了年级预赛,四个小组的平均分相同,若要从中选择出一个各成员实力更平均的小组代表年级参加学校决赛,那么应选( )
甲 乙 丙 丁
方差 3.6 3.2 4 4.3
A.甲组 B.乙组 C.丙组 D.丁组
2.要选派参加数学竞赛的选手,经过三轮初赛,甲、乙、丙、丁四位选手的平均成绩都是86分,方差分别是=1.5,=2.6,=3.5,=2.9,若从中选一位发挥稳定的选手参加决赛,你认为应该派( )
A.甲 B.乙 C.丙 D.丁
3.某校八年级一、二班学生参加同一次数学考试,统计成绩后得到下表:
班级 参加人数 中位数 方差 平均数
一班 55 78 135 75
二班 55 81 126 75
张老师根据上表,对本次考试得出如下结论:①一、二两班学生的平均水平相同;②二班的优秀人数多于一班的优秀人数(成绩≥80分为优秀);③一班成绩波动情况比二班成绩波动大.上述结论正确的是( )
A.①②③ B.①② C.①③ D.②③
4.某同学对数据24,48,23,24,5■,52进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.方差 B.众数 C.平均数 D.中位数
5.(2019河北保定三模)某工厂六台机床第一天和第二天生产的零件数分别如图1和图2所示,则与第一天相比,这六台机床第二天生产零件的平均数与方差的变化是( )
图1
图2
A.平均数变大,方差不变
B.平均数变小,方差变大
C.平均数不变,方差变小
D.平均数不变,方差变大
二、填空题
6.某组数据方差的计算公式是s2=[(x1-4)2+(x2-4)2+…+(x10-4)2],则该组数据的总和为 .
7.2020年发布的《云南省初中学生学业水平体育科目考试办法》中,篮球成为三项技能类考试项目之一.某学校甲、乙两名同学做了10次定点投篮训练(每次训练投5个),每次训练成绩(投中的个数)如图所示,则甲、乙两名同学投篮成绩比较稳定的是 (填“甲”或“乙”).
8.某果农随机从甲、乙、丙三个品种的枇杷树中各选5棵,每棵产量的平均数(单位:千克)及方差s2如表所示,他准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是 .
甲 乙 丙
45 45 42
s2 1.8 2.3 1.8
9.(2020北京清华大学附中分校期末)小天想要计算一组数据92,90,94,86,99,85的方差,在计算平均数的过程中,将这组数据中的每一个数都减去90,得到一组新数据2,0,4,-4,9,-5,记这组新数据的方差为,则= (结果保留两位小数), (填“>”“=”或“<”).
10.(2020浙江杭州期中)据统计,某车间10名员工日平均生产零件的个数为8,方差为2.5.引入新技术后,每名员工每天都比原来多生产1个零件,则现在日平均生产零件个数为 ,方差为 .
三、解答题
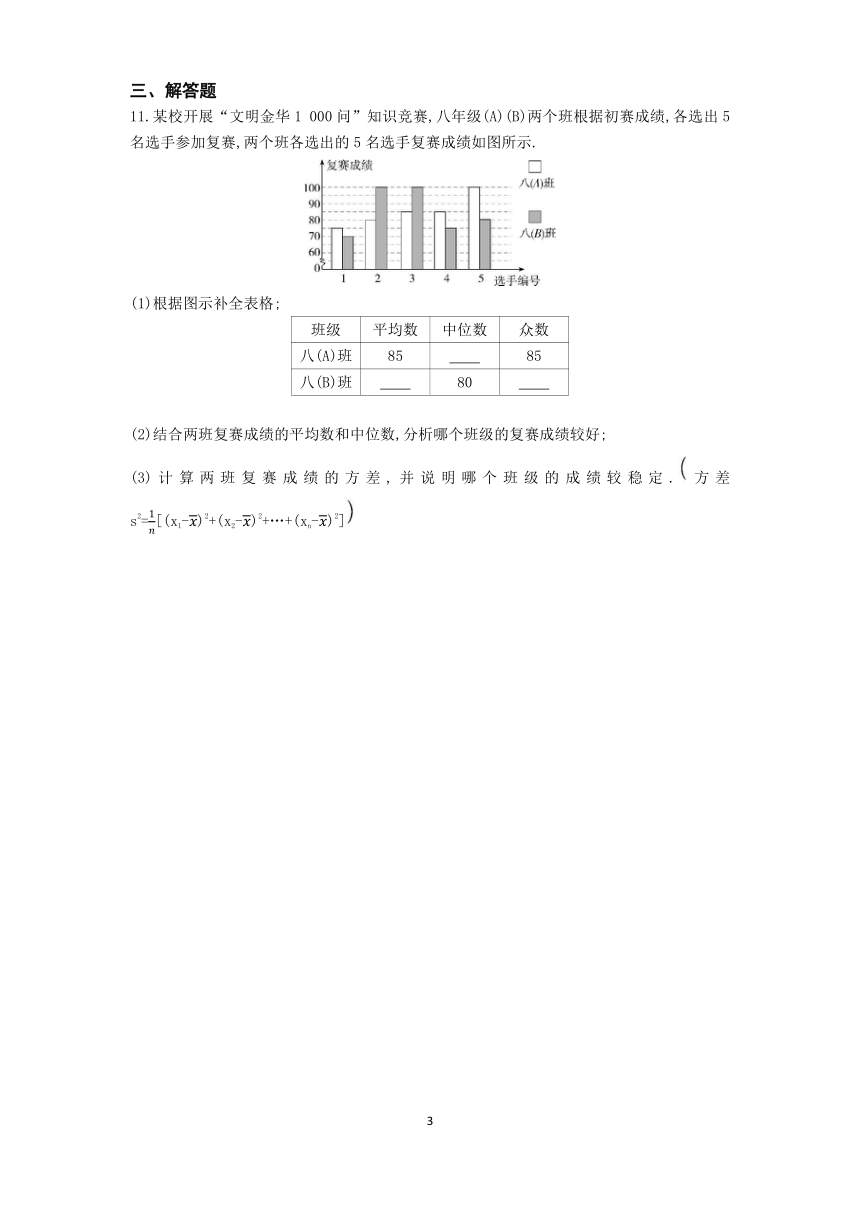
11.某校开展“文明金华1 000问”知识竞赛,八年级(A)(B)两个班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手复赛成绩如图所示.
(1)根据图示补全表格;
班级 平均数 中位数 众数
八(A)班 85 85
八(B)班 80
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班级的成绩较稳定.方差s2=[(x1-)2+(x2-)2+…+(xn-)2]
12.在一次数学实践作业中,甲、乙两组学生各自对学校旗杆进行了5次测量,所得数据(单位:米)如下:
甲组测得的高度分别为12.00,11.90,12.05,12.00,12.05;
乙组测得的高度分别为11.95,12.05,12.00,11.95,12.05.
(1)请整理以上数据,补全下表:
测得的旗杆高度(米) 11.90 11.95 12.00 12.05
甲测得的次数 1 0 2 2
乙测得的次数 0 2
(2)现已算得乙组所得数据的平均数=12.00,方差=0.002,求甲组所得数据的中位数和平均数;
(3)请通过计算说明哪一组所测得的旗杆高度比较一致.
初中数学·人教版·八年级下册——第二十章 数据的分析
20.2 数据的波动程度
测试时间:20分钟
一、选择题
1.答案 B 由题表可得<<<,
∴若要从中选择出一个各成员实力更平均的小组代表年级参加学校决赛,则应选乙组.
故选B.
2.答案 A ∵=1.5,=2.6,=3.5,=2.9,
∴<<<,∴甲发挥更稳定.故选A.
3.答案 A ①一、二两班学生的平均水平相同,说法正确;
②二班的优秀人数多于一班的优秀人数(成绩≥80分为优秀),说法正确;
③一班成绩波动情况比二班成绩波动大,说法正确.
故选A.
4.答案 D 这组数据的平均数、方差和众数都与被涂污数字有关,而这组数据的中位数为24与48的平均数,与被涂污数字无关.
故选D.
5.答案 D 根据统计图可知,第一天生产零件的平均数是m,第二天生产零件的平均数是m,所以平均数不变,但方差变大.故选D.
二、填空题
6.答案 40
解析 由s2=[(x1-4)2+(x2-4)2+…+(x10-4)2]知共有10个数据,这10个数据的平均数为4,
则该组数据的总和为10×4=40.
7.答案 乙
解析 由题图知,甲这10次成绩偏离平均数大,即波动大,而乙这10次成绩分布比较集中,即波动小,则<,故两人的成绩比较稳定的是乙.
8.答案 甲
解析 因为甲、乙的平均数比丙大,所以甲、乙的产量较高,
又甲的方差比乙小,所以甲的产量比较稳定,
故从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,应选的品种是甲.
9.答案 22.67;=
解析 新数据2,0,4,-4,9,-5的平均数为(2+0+4-4+9-5)÷6=1,则=×[(2-1)2+(0-1)2+(4-1)2+(-4-1)2+(9-1)2+(-5-1)2]≈22.67.
因为一组数据中的每一个数据都加上(或减去)同一个常数后,方差不变,所以=.
10.答案 9;2.5
解析 现在日平均生产零件的个数为=9.
设原来每名员工日平均生产零件的个数分别为x1,x2,…,x10,
∴原来的方差为[(x1-8)2+(x2-8)2+…+(x10-8)2]=2.5,
∴现在的方差为
[(x1+1-9)2+(x2+1-9)2+…+(x10+1-9)2]=[(x1-8)2+(x2-8)2+…+(x10-8)]2=2.5.
故答案为9;2.5.
三、解答题
11.解析 (1)观察统计图可知,八(B)班5名选手复赛成绩为70、100、100、75、80,则八(B)班5名选手的平均成绩为(70+100+100+75+80)÷5=85.
又100出现的次数最多,所以众数是100.
∵八(A)班5名选手复赛成绩由低到高依次为75、80、85、85、100,
∴这组数据中位数是85.
补全表格如下:
班级 平均数 中位数 众数
八(A)班 85 85 85
八(B)班 85 80 100
(2)由(1)可知,两个班复赛成绩的平均数一样,八(A)班复赛成绩的中位数高于八(B)班,
所以八(A)班的复赛成绩较好.
(3)=×[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70,
=×[(70-85)2+(100-85)2+(100-85)2+(75-85)2+(80-85)2]=160,
因为70<160,所以八(A)班成绩较稳定.
12.解析 (1)补全表格如下:
测得的旗杆高度(米) 11.90 11.95 12.00 12.05
甲测得的次数 1 0 2 2
乙测得的次数 0 2 1 2
(2)将甲组数据从小到大排列为11.90,12.00,12.00,12.05,12.05,
∴甲组学生所测得数据的中位数是12.00,
平均数==12.00.
(3)=×[(11.90-12.00)2+2×(12.00-12.00)2+2×(12.05-12.00)2]=0.003,
∵>,∴乙组学生所测得的旗杆高度比较一致.
6
20.2 数据的波动程度
测试时间:20分钟
一、选择题
1.2021年正值中国共产党建党100周年,某校开展“致敬建党百年,传承红色基因”党史知识竞赛活动.八年级甲、乙、丙、丁四个小组的同学分别参加了年级预赛,四个小组的平均分相同,若要从中选择出一个各成员实力更平均的小组代表年级参加学校决赛,那么应选( )
甲 乙 丙 丁
方差 3.6 3.2 4 4.3
A.甲组 B.乙组 C.丙组 D.丁组
2.要选派参加数学竞赛的选手,经过三轮初赛,甲、乙、丙、丁四位选手的平均成绩都是86分,方差分别是=1.5,=2.6,=3.5,=2.9,若从中选一位发挥稳定的选手参加决赛,你认为应该派( )
A.甲 B.乙 C.丙 D.丁
3.某校八年级一、二班学生参加同一次数学考试,统计成绩后得到下表:
班级 参加人数 中位数 方差 平均数
一班 55 78 135 75
二班 55 81 126 75
张老师根据上表,对本次考试得出如下结论:①一、二两班学生的平均水平相同;②二班的优秀人数多于一班的优秀人数(成绩≥80分为优秀);③一班成绩波动情况比二班成绩波动大.上述结论正确的是( )
A.①②③ B.①② C.①③ D.②③
4.某同学对数据24,48,23,24,5■,52进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.方差 B.众数 C.平均数 D.中位数
5.(2019河北保定三模)某工厂六台机床第一天和第二天生产的零件数分别如图1和图2所示,则与第一天相比,这六台机床第二天生产零件的平均数与方差的变化是( )
图1
图2
A.平均数变大,方差不变
B.平均数变小,方差变大
C.平均数不变,方差变小
D.平均数不变,方差变大
二、填空题
6.某组数据方差的计算公式是s2=[(x1-4)2+(x2-4)2+…+(x10-4)2],则该组数据的总和为 .
7.2020年发布的《云南省初中学生学业水平体育科目考试办法》中,篮球成为三项技能类考试项目之一.某学校甲、乙两名同学做了10次定点投篮训练(每次训练投5个),每次训练成绩(投中的个数)如图所示,则甲、乙两名同学投篮成绩比较稳定的是 (填“甲”或“乙”).
8.某果农随机从甲、乙、丙三个品种的枇杷树中各选5棵,每棵产量的平均数(单位:千克)及方差s2如表所示,他准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是 .
甲 乙 丙
45 45 42
s2 1.8 2.3 1.8
9.(2020北京清华大学附中分校期末)小天想要计算一组数据92,90,94,86,99,85的方差,在计算平均数的过程中,将这组数据中的每一个数都减去90,得到一组新数据2,0,4,-4,9,-5,记这组新数据的方差为,则= (结果保留两位小数), (填“>”“=”或“<”).
10.(2020浙江杭州期中)据统计,某车间10名员工日平均生产零件的个数为8,方差为2.5.引入新技术后,每名员工每天都比原来多生产1个零件,则现在日平均生产零件个数为 ,方差为 .
三、解答题
11.某校开展“文明金华1 000问”知识竞赛,八年级(A)(B)两个班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手复赛成绩如图所示.
(1)根据图示补全表格;
班级 平均数 中位数 众数
八(A)班 85 85
八(B)班 80
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班级的成绩较稳定.方差s2=[(x1-)2+(x2-)2+…+(xn-)2]
12.在一次数学实践作业中,甲、乙两组学生各自对学校旗杆进行了5次测量,所得数据(单位:米)如下:
甲组测得的高度分别为12.00,11.90,12.05,12.00,12.05;
乙组测得的高度分别为11.95,12.05,12.00,11.95,12.05.
(1)请整理以上数据,补全下表:
测得的旗杆高度(米) 11.90 11.95 12.00 12.05
甲测得的次数 1 0 2 2
乙测得的次数 0 2
(2)现已算得乙组所得数据的平均数=12.00,方差=0.002,求甲组所得数据的中位数和平均数;
(3)请通过计算说明哪一组所测得的旗杆高度比较一致.
初中数学·人教版·八年级下册——第二十章 数据的分析
20.2 数据的波动程度
测试时间:20分钟
一、选择题
1.答案 B 由题表可得<<<,
∴若要从中选择出一个各成员实力更平均的小组代表年级参加学校决赛,则应选乙组.
故选B.
2.答案 A ∵=1.5,=2.6,=3.5,=2.9,
∴<<<,∴甲发挥更稳定.故选A.
3.答案 A ①一、二两班学生的平均水平相同,说法正确;
②二班的优秀人数多于一班的优秀人数(成绩≥80分为优秀),说法正确;
③一班成绩波动情况比二班成绩波动大,说法正确.
故选A.
4.答案 D 这组数据的平均数、方差和众数都与被涂污数字有关,而这组数据的中位数为24与48的平均数,与被涂污数字无关.
故选D.
5.答案 D 根据统计图可知,第一天生产零件的平均数是m,第二天生产零件的平均数是m,所以平均数不变,但方差变大.故选D.
二、填空题
6.答案 40
解析 由s2=[(x1-4)2+(x2-4)2+…+(x10-4)2]知共有10个数据,这10个数据的平均数为4,
则该组数据的总和为10×4=40.
7.答案 乙
解析 由题图知,甲这10次成绩偏离平均数大,即波动大,而乙这10次成绩分布比较集中,即波动小,则<,故两人的成绩比较稳定的是乙.
8.答案 甲
解析 因为甲、乙的平均数比丙大,所以甲、乙的产量较高,
又甲的方差比乙小,所以甲的产量比较稳定,
故从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,应选的品种是甲.
9.答案 22.67;=
解析 新数据2,0,4,-4,9,-5的平均数为(2+0+4-4+9-5)÷6=1,则=×[(2-1)2+(0-1)2+(4-1)2+(-4-1)2+(9-1)2+(-5-1)2]≈22.67.
因为一组数据中的每一个数据都加上(或减去)同一个常数后,方差不变,所以=.
10.答案 9;2.5
解析 现在日平均生产零件的个数为=9.
设原来每名员工日平均生产零件的个数分别为x1,x2,…,x10,
∴原来的方差为[(x1-8)2+(x2-8)2+…+(x10-8)2]=2.5,
∴现在的方差为
[(x1+1-9)2+(x2+1-9)2+…+(x10+1-9)2]=[(x1-8)2+(x2-8)2+…+(x10-8)]2=2.5.
故答案为9;2.5.
三、解答题
11.解析 (1)观察统计图可知,八(B)班5名选手复赛成绩为70、100、100、75、80,则八(B)班5名选手的平均成绩为(70+100+100+75+80)÷5=85.
又100出现的次数最多,所以众数是100.
∵八(A)班5名选手复赛成绩由低到高依次为75、80、85、85、100,
∴这组数据中位数是85.
补全表格如下:
班级 平均数 中位数 众数
八(A)班 85 85 85
八(B)班 85 80 100
(2)由(1)可知,两个班复赛成绩的平均数一样,八(A)班复赛成绩的中位数高于八(B)班,
所以八(A)班的复赛成绩较好.
(3)=×[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70,
=×[(70-85)2+(100-85)2+(100-85)2+(75-85)2+(80-85)2]=160,
因为70<160,所以八(A)班成绩较稳定.
12.解析 (1)补全表格如下:
测得的旗杆高度(米) 11.90 11.95 12.00 12.05
甲测得的次数 1 0 2 2
乙测得的次数 0 2 1 2
(2)将甲组数据从小到大排列为11.90,12.00,12.00,12.05,12.05,
∴甲组学生所测得数据的中位数是12.00,
平均数==12.00.
(3)=×[(11.90-12.00)2+2×(12.00-12.00)2+2×(12.05-12.00)2]=0.003,
∵>,∴乙组学生所测得的旗杆高度比较一致.
6
