黑龙江省哈尔滨市香坊区德强学校2020-2021学年八年级(下)4月月考数学试卷(word解析版)
文档属性
| 名称 | 黑龙江省哈尔滨市香坊区德强学校2020-2021学年八年级(下)4月月考数学试卷(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 22:48:42 | ||
图片预览


文档简介
黑龙江省哈尔滨市香坊区德强学校2020-2021学年八年级(下)月考数学试卷(4月份)(五四学制)
一、选择题(本大题共10小题,共30.0分)
下列四边形中不是轴对称图形的是
A. 矩形 B. 菱形
C. 正方形 D. 平行四边形
下列计算正确的是
A. B. C. D.
如图,中,,为边中点,连接,则
A.
B.
C.
D.
菱形两条对角线、长分别是和,则菱形的面积为
A. B. C. D.
如图,要从电线杆离地面处向地面拉一条长为的钢缆,则地面钢缆固定点到电线杆底部点的距离是
A.
B.
C.
D.
菱形中,如果、、、分别是各边的中点,那么四边形的形状是
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
分式方程的解是
A. B. C. D.
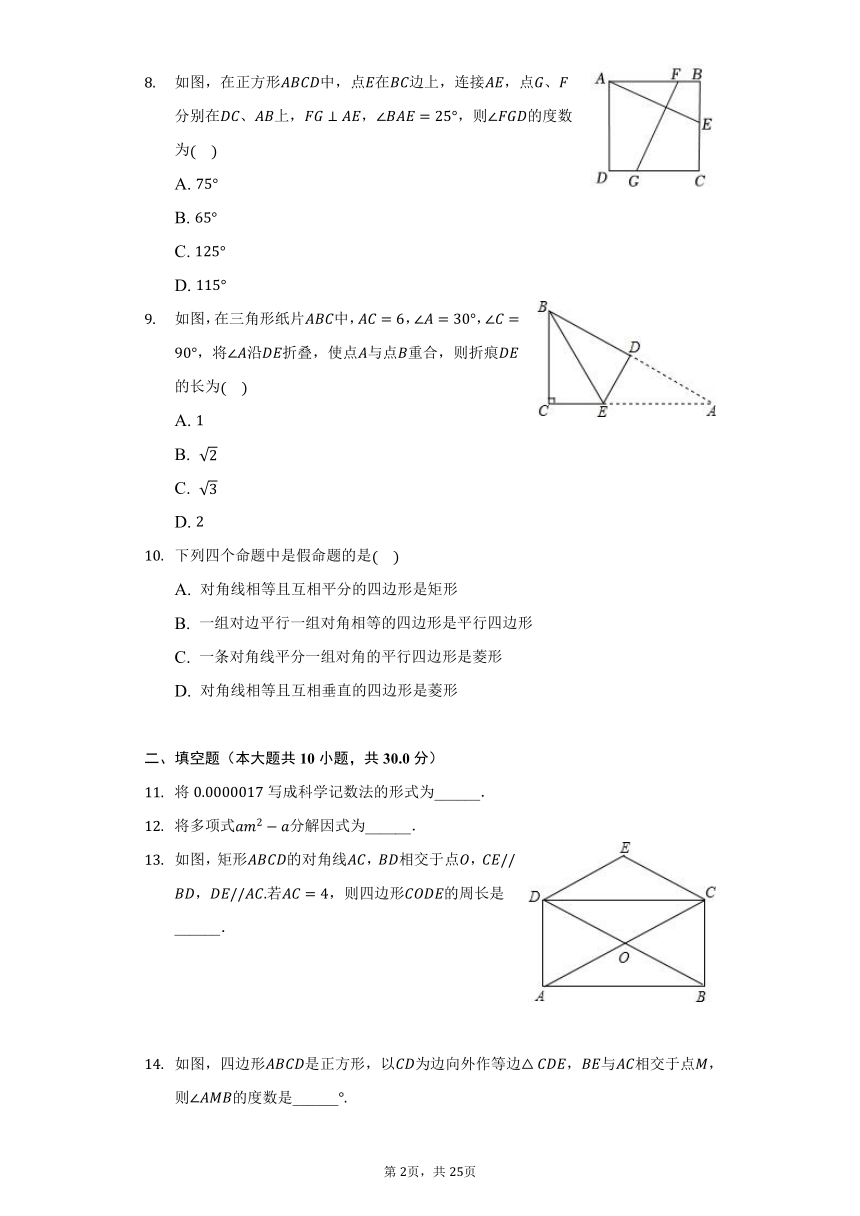
如图,在正方形中,点在边上,连接,点、分别在、上,,,则的度数为
A.
B.
C.
D.
如图,在三角形纸片中,,,,将沿折叠,使点与点重合,则折痕的长为
A.
B.
C.
D.
下列四个命题中是假命题的是
A. 对角线相等且互相平分的四边形是矩形
B. 一组对边平行一组对角相等的四边形是平行四边形
C. 一条对角线平分一组对角的平行四边形是菱形
D. 对角线相等且互相垂直的四边形是菱形
二、填空题(本大题共10小题,共30.0分)
将写成科学记数法的形式为______.
将多项式分解因式为______.
如图,矩形的对角线,相交于点,,若,则四边形的周长是______.
如图,四边形是正方形,以为边向外作等边,与相交于点,则的度数是______
如图,在平行四边形中,,,,则平行四边形的面积是______.
如图,在中,,于点,,是斜边的中点,的度数是______
如图,和都是等腰直角三角形,,,的顶点在的斜边上,若,,则______.
在矩形中,,,点在边上,点在边上,连接、,若,,则的长为______.
如图,在四边形中,,,点、分别是四边形对角线、的中点,则的长度为______.
如图,四边形中,,,过点作于点,连接,若,,,则的长为______.
三、解答题(本大题共7小题,共60.0分)
先化简再求值.,其中.
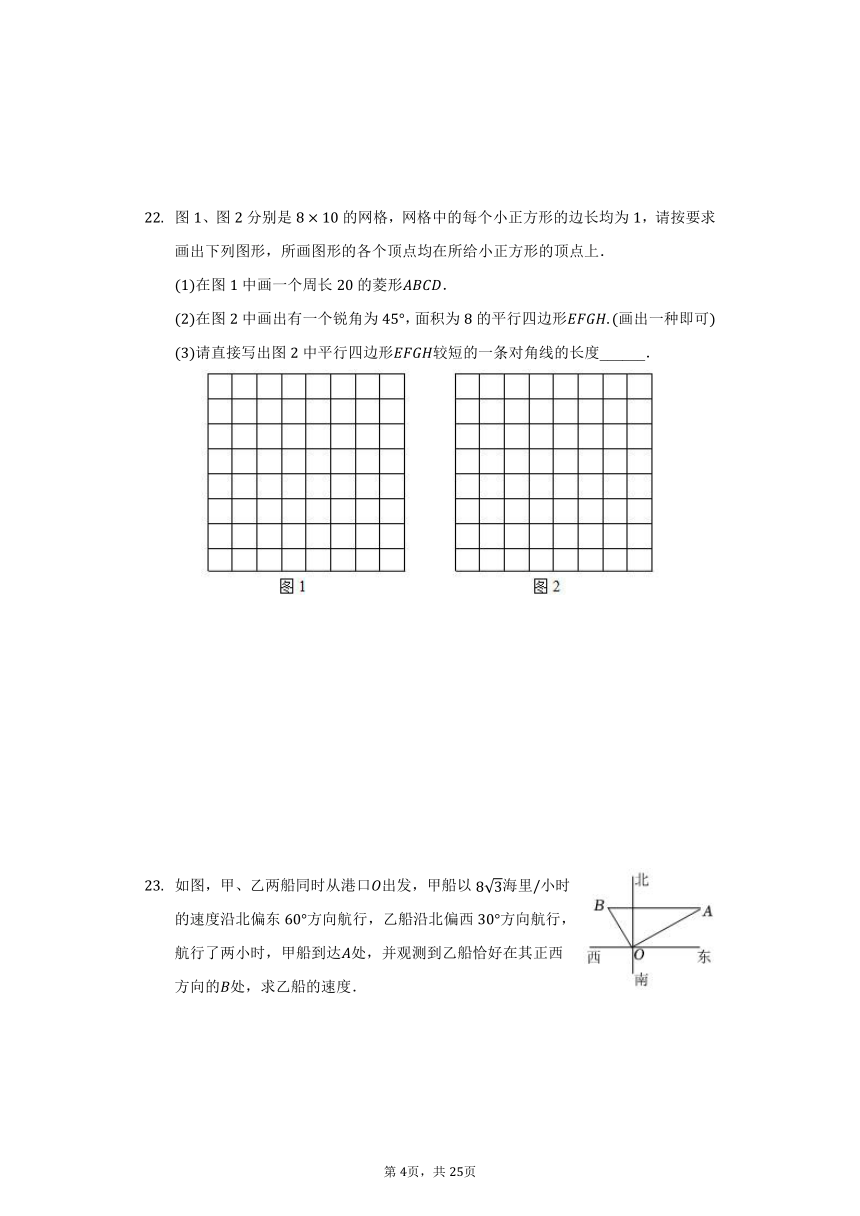
图、图分别是的网格,网格中的每个小正方形的边长均为,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上.
在图中画一个周长的菱形.
在图中画出有一个锐角为,面积为的平行四边形画出一种即可
请直接写出图中平行四边形较短的一条对角线的长度______.
如图,甲、乙两船同时从港口出发,甲船以海里小时的速度沿北偏东方向航行,乙船沿北偏西方向航行,航行了两小时,甲船到达处,并观测到乙船恰好在其正西方向的处,求乙船的速度.
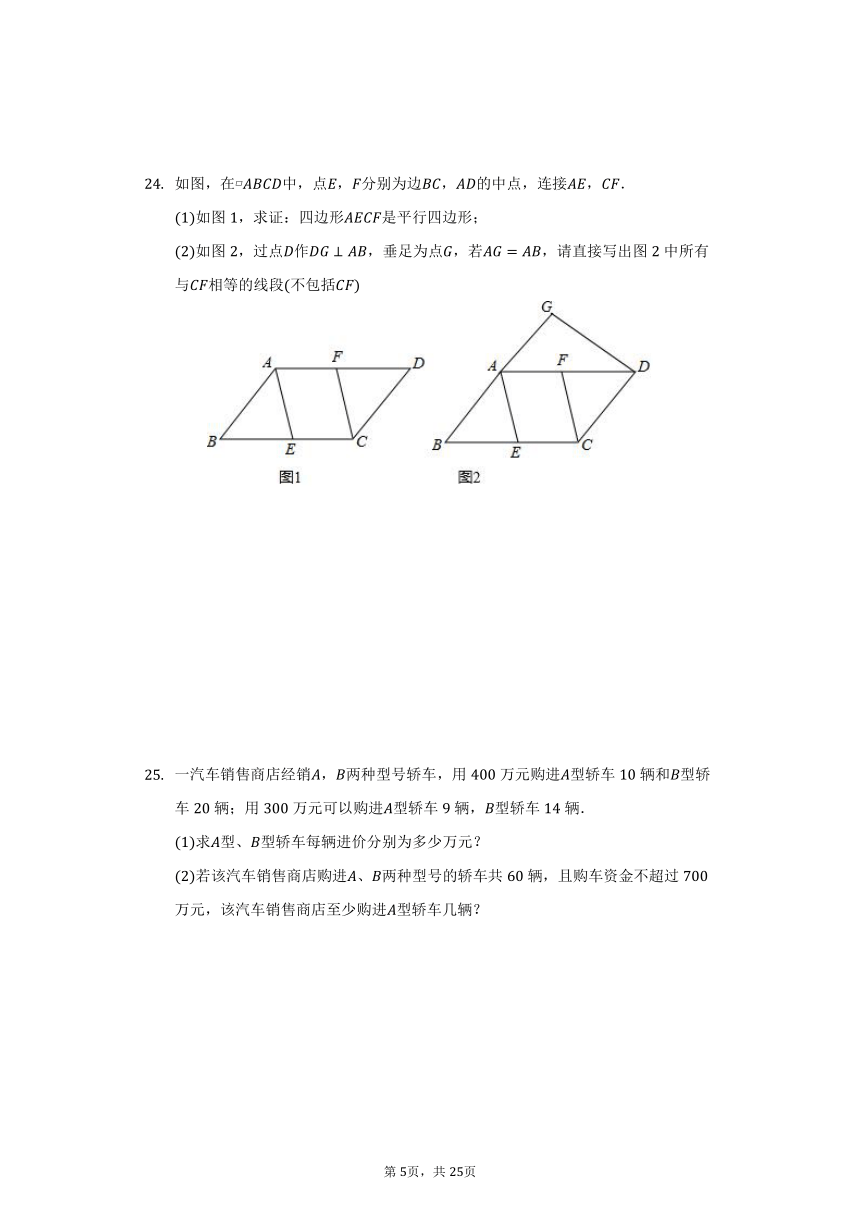
如图,在 中,点,分别为边,的中点,连接,.
如图,求证:四边形是平行四边形;
如图,过点作,垂足为点,若,请直接写出图中所有与相等的线段不包括
一汽车销售商店经销,两种型号轿车,用万元购进型轿车辆和型轿车辆;用万元可以购进型轿车辆,型轿车辆.
求型、型轿车每辆进价分别为多少万元?
若该汽车销售商店购进、两种型号的轿车共辆,且购车资金不超过万元,该汽车销售商店至少购进型轿车几辆?
如图,菱形,连接对角线,过点作于点,交于点,连接,若.
如图,求证:;
如图,连接,求证:;
如图,过点作的垂线,分别交延长线于点、延长线于点,若,,求:的值.
如图,在平面直角坐标系中,点为坐标原点,直线分别交轴正半轴于点,交轴负半轴于点,过点作,且.
求点的坐标.
过点作轴,垂足为,是线段上一个动点,过点作轴,垂足为点,在延长线上取点,在轴点右侧取点,连接,在线段上取点,连接,使,设线段,满足的面积表示为,求线段的长度.
在的条件下,连接并延长交轴于点,当为中点时,连接,过点作,在轴左侧直线上是否存在点,连接、,使得与以、、为三边长的三角形全等?若存在,求出的长,若不存在,请说明理由.
答案和解析
1.【答案】
【解析】解:、矩形是轴对称图形,又是中心对称图形,故选项错误;
B、菱形既是轴对称图形,又是中心对称图形,故选项错误;
C、正方形是轴对称图形,又是中心对称图形,故选项错误;
D、平行四边形是中心对称图形,不是轴对称图形,故选项正确;
故选:.
根据中心对称图形以及轴对称图形的定义即可作出判断.
本题主要考查了中心对称图形与轴对称图形的定义,正确理解定义是解题关键.
2.【答案】
【解析】解:、,故A不符合题意;
B、,故B符合题意;
C、,故C不符合题意;
D、,故D不符合题意;
故选:.
利用幂的乘方与积的乘方的法则,同底数幂的乘法的法则,同底数幂的除法的法则对各项进行运算即可.
本题主要考查幂的乘方的与积的乘方,同底数幂的乘法,同底数幂的除法,解答的关键是对相应的运算法则的掌握.
3.【答案】
【解析】解:在中,,是的中点,
线段是斜边上的中线;
又,
.
故选:.
根据直角三角形斜边上的中线等于斜边的一半解答.
本题考查了直角三角形斜边上的中线.熟记直角三角形斜边上的中线等于斜边的一半是解题的关键.
4.【答案】
【解析】解:菱形的面积:,
故选:.
根据菱形的面积公式:菱形面积、是两条对角线的长度可得到答案.
此题主要考查了菱形的面积公式,关键是熟练掌握面积公式.
5.【答案】
【解析】解:由勾股定理得:,
故选:.
根据勾股定理求出即可.
本题考查了勾股定理的应用,能熟记勾股定理的内容是解此题的关键.
6.【答案】
【解析】解:菱形中,如果、、、分别是各边的中点,
由中位线定理可得,所得四边形的对边平行且相等,则此四边形为平行四边形;
又因为菱形的对角线互相垂直平分,可求得四边形的一角为,
所以连接菱形各边中点的四边形是矩形,
即四边形的形状是矩形.
故选:.
利用中点四边形的定义得出,以及矩形的判定:有一角为的平行四边形是矩形,得出菱形中点四边形的形状.
此题主要考查了矩形的判定定理:有一个角是直角的平行四边形是矩形;有三个角是直角的四边形是矩形;对角线互相平分且相等的四边形是矩形.
7.【答案】
【解析】解:去分母得:,
解得:,
检验:把代入得:,
分式方程的解为.
故选:.
分式方程去分母转化为整式方程,求出整式方程的解得到的值,经检验即可得到分式方程的解.
此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.
8.【答案】
【解析】解:过作于,交于,
四边形是正方形,
,,
,
,
,
,,
,
故选:.
方法二:,
,
,
,
四边形是正方形,
,
,
,
故选:.
过作于,交于,证得,根据三角形外角定理即可求出.
本题主要考查了正方形的性质,直角三角形的两锐角互余,根据直角三角形的两锐角互余证得是解决问题的关键.
9.【答案】
【解析】解:,,
.
将沿折叠,使点与点重合,
.
,,,
≌.
,,
.
,即.
故选:.
本题主要考查的是翻折的性质、勾股定理的应用,利用翻折的性质得到从而证出≌,根据勾股定理,含角的直角三角形的性质即可求得.
10.【答案】
【解析】解:、对角线相等且互相平分的四边形是矩形,本选项说法是真命题;
B、一组对边平行一组对角相等的四边形是平行四边形,本选项说法是真命题;
C、一条对角线平分一组对角的平行四边形是菱形,本选项说法是真命题;
D、对角线互相平分且互相垂直的四边形是菱形,本选项说法是假命题;
故选:.
根据矩形、平行四边形、菱形的判定定理判断即可.
本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
11.【答案】
【解析】解:将写成科学记数法的形式为.
故答案为:.
绝对值小于的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的的个数所决定.
12.【答案】
【解析】解:
,
故答案为:.
先提公因式,然后利用平方差公式分解即可解答.
本题考查了提公因式法与公式法的综合运用,一定要注意如果多项式的各项含有公因式,必须先提公因式.
13.【答案】
【解析】解:,,
四边形是平行四边形,
四边形是矩形,
,,,
,
四边形是菱形,
,
四边形的周长;
故答案为:.
先证明四边形是平行四边形,再根据矩形的性质得出,然后证明四边形是菱形,即可求出周长.
本题考查了菱形的判定与性质以及矩形的性质;证明四边形是菱形是解决问题的关键.
14.【答案】
【解析】解:四边形是正方形,是等边三角形,
,,
,
,
,
.
,
故答案为:.
先证明为等腰三角形,从而可取得的度数,然后依据三角形内角和定理求出的度数,进而可以解决问题.
本题主要考查的是正方形的性质、等边三角形的性质、等腰三角形的性质,熟练掌握相关图形的性质是解题的关键.
15.【答案】
【解析】解: 中,,,
,,
,
,
是直角三角形,即,
.
故答案为:.
由 中,,,,求得,的长,利用勾股定理的逆定理即可证得是直角三角形,继而求得答案.
此题考查了平行四边形的性质以及勾股定理的逆定理.注意证得是直角三角形是关键.
16.【答案】
【解析】解:,,,
,
,
则,
,
,
,
是斜边的中点,
,
,
,
故答案为:.
先根据已知条件求出和的度数,再根据是斜边的中点,得出,从而得出结论.
本题考查了直角三角形斜边上的中线的性质以及角的运算,关键是对角的和差的运算.
17.【答案】
【解析】解:连接,如图,
和都是等腰直角三角形,,,
,,,
,
在和中,
,
≌,
,,
,
是直角三角形,
,
是等腰直角三角形,,
,
,
解得:负值已舍去,
故答案为:.
连接,证≌,得,,再证证明是直角三角形,然后由勾股定理求出的长,即可得出的长.
本题考查了全等三角形的判定与性质、等腰直角三角形的性质、勾股定理等知识,熟练掌握等腰直角三角形的性质,证明三角形全等是解题的关键.
18.【答案】或
【解析】解:如图所示:
作于点,则,
四边形为矩形,
,,
四边形为矩形,
,
,
,
,
,
,
;
如图所示:
作于点,则,
四边形为矩形,
,,
四边形为矩形,
,
,
,
,
,
,
,
故答案为:或.
根据矩形的性质和勾股定理,分两种情况解答即可.
此题考查矩形的性质,关键是根据矩形的性质得出对边相等解答.
19.【答案】
【解析】解:取的中点,连接,,
为的中点,
是的中位线,
,,
为的中点,
是的中位线,
,,
,
,
,
,
,即,
,
故答案为:.
取的中点,连接,,理由三角形的中位线可求解,结合可得,再利用勾股定理可求解的长.
本题主要考查三角形的中位线,勾股定理,求解,的值是解题的关键.
20.【答案】
【解析】解:,
,,,四点共圆,
,
,
,
,
,
作于点,
,
≌,
,,
,,
≌,
,
,
即,
设,,
,,
,
,
在中,,
即,
解得:,
,,
,
,
故答案为:.
根据全等三角形的判定和性质得出,,进而利用勾股定理解答即可.
此题考查全等三角形的判定和性质,关键是根据全等三角形的判定和性质解答.
21.【答案】解;原式
,
当时,原式.
【解析】先根据分式混合运算的法则把原式进行化简,再把的值代入进行计算即可.
本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.
22.【答案】
【解析】解:如图中,菱形即为所求.
如图中,平行四边形即为所求.
图中平行四边形较短的一条对角线的长度为.
故答案为:.
构造边长为的菱形即可;
构造底为,高为,有一个角是的平行四边形即可;
根据网格利用勾股定理即可求出图中平行四边形较短的一条对角线的长度.
本题考查作图应用与设计,平行四边形的判定和性质,菱形的判定和性质等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.
23.【答案】解:由已知可得:海里,
又已知甲船以海里时的速度沿北偏东方向航行,乙船沿北偏西,
,
又乙船正好到达甲船正西方向的点,
,
海里,
所以乙船的速度为:海里小时,
答:乙船的速度为海里小时.
【解析】本题可以求出甲船行进的距离,根据三角函数就可以求出,就可以求出乙船的速度.
本题主要考查的是解直角三角形的应用方向角问题及三角函数的定义,理解方向角的定义是解决本题的关键.
24.【答案】解:如图中,
四边形是平行四边形,
,,
点,分别为边,的中点,
,,
,,
四边形是平行四边形.
如图中,连接
,,
四边形是矩形,
,
四边形是矩形.
,,
,,
与相等的相等有,,,,.
【解析】只要证明,即可;
如图中,连接首先证明四边形是矩形.推出由,,可得,;
本题考查平行四边形的判定和性质、矩形的判定和性质、直角三角形斜边中线定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
25.【答案】解:设型号的轿车每辆进价为万元,型号的轿车每辆进价为万元.
根据题意得,
解得.
答:设型号的轿车每辆进价为万元,型号的轿车每辆进价为万元.
设汽车销售商店至少购进型轿车辆,则型轿车辆,由题意得,
,
解得:.
答:该汽车销售商店至少购进型轿车辆.
【解析】等量关系为:辆轿车的价钱辆轿车的价钱万元;辆轿车的价钱辆轿车的价钱万元;
根据中求出、轿车的单价,然后根据关键语“用不超过万元购进、两种型号轿车共辆”列出不等式,解出不等式即可.
此题考查二元一次方程组和一元一次不等式的运用,找出题目蕴含的数量关系是解决问题的关键.
26.【答案】证明:设,
四边形是菱形,
,,
,
,,
,
,
,
,
;
证明:四边形是菱形,
,,
又,
≌,
,
;
解:,,
,
,
四边形是平行四边形,
,
,
,
,
,
,
,
,
,,
,
,
,
,
:.
【解析】由菱形的性质可得,由余角的性质可求,可得;
由“”可证≌,可得,可得结论;
利用勾股定理和面积法分别求出,,的长,即可求解.
本题是四边形综合题,考查了菱形的性质,全等三角形的判定和性质,勾股定理等知识,利用勾股定理计算出的长是解题的关键.
27.【答案】解:如图,点,交轴负半轴于点,
,,
过点作轴于,则,
,
,
,
,
,
,
≌,
,,
,
;
如图,,
,
,
,
轴,
,
,
,
的面积为,
,
;
在轴左侧直线上是存在点,使得与以、、为三边长的三角形全等,
如图,
轴,轴,
,
是直角三角形,
与以、、为三边长的三角形全等,
、、构成的三角形为直角三角形,
过点作轴于,则,由知,,
,
轴,轴,
,
轴,
轴,
,
为中点,
,
≌,
,
,
由知,,
,
记与轴的交点为,则四边形为矩形,
,
,
,
点在线段上,
,
,
是公共边,
与是对应边,且是斜边,即,
设,则点,,
,,
、、构成的三角形为直角三角形,
,
,
,
,
即:.
【解析】过点作轴,进而判断出≌,得出,,即可求出答案;
先判断出,进而判断出,再用的面积为建立方程求解,即可求出答案;
先判断出、、构成的三角形为直角三角形,过点作轴于,进而判断出≌,得出,求出,由知,,,记与轴的交点为,则四边形为矩形,进而求出,,进而判断出,进而判断出与是对应边,且是斜边,设,表示出点,的坐标,再利用勾股定理建立方程求出的值,即可求出答案.
此题是一次函数综合题,主要考查了全等三角形的判定和性质,三角形的面积公式,等腰直角三角形的性质,勾股定理,判断出为斜边是解本题的关键.
第2页,共2页
第1页,共1页
一、选择题(本大题共10小题,共30.0分)
下列四边形中不是轴对称图形的是
A. 矩形 B. 菱形
C. 正方形 D. 平行四边形
下列计算正确的是
A. B. C. D.
如图,中,,为边中点,连接,则
A.
B.
C.
D.
菱形两条对角线、长分别是和,则菱形的面积为
A. B. C. D.
如图,要从电线杆离地面处向地面拉一条长为的钢缆,则地面钢缆固定点到电线杆底部点的距离是
A.
B.
C.
D.
菱形中,如果、、、分别是各边的中点,那么四边形的形状是
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
分式方程的解是
A. B. C. D.
如图,在正方形中,点在边上,连接,点、分别在、上,,,则的度数为
A.
B.
C.
D.
如图,在三角形纸片中,,,,将沿折叠,使点与点重合,则折痕的长为
A.
B.
C.
D.
下列四个命题中是假命题的是
A. 对角线相等且互相平分的四边形是矩形
B. 一组对边平行一组对角相等的四边形是平行四边形
C. 一条对角线平分一组对角的平行四边形是菱形
D. 对角线相等且互相垂直的四边形是菱形
二、填空题(本大题共10小题,共30.0分)
将写成科学记数法的形式为______.
将多项式分解因式为______.
如图,矩形的对角线,相交于点,,若,则四边形的周长是______.
如图,四边形是正方形,以为边向外作等边,与相交于点,则的度数是______
如图,在平行四边形中,,,,则平行四边形的面积是______.
如图,在中,,于点,,是斜边的中点,的度数是______
如图,和都是等腰直角三角形,,,的顶点在的斜边上,若,,则______.
在矩形中,,,点在边上,点在边上,连接、,若,,则的长为______.
如图,在四边形中,,,点、分别是四边形对角线、的中点,则的长度为______.
如图,四边形中,,,过点作于点,连接,若,,,则的长为______.
三、解答题(本大题共7小题,共60.0分)
先化简再求值.,其中.
图、图分别是的网格,网格中的每个小正方形的边长均为,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上.
在图中画一个周长的菱形.
在图中画出有一个锐角为,面积为的平行四边形画出一种即可
请直接写出图中平行四边形较短的一条对角线的长度______.
如图,甲、乙两船同时从港口出发,甲船以海里小时的速度沿北偏东方向航行,乙船沿北偏西方向航行,航行了两小时,甲船到达处,并观测到乙船恰好在其正西方向的处,求乙船的速度.
如图,在 中,点,分别为边,的中点,连接,.
如图,求证:四边形是平行四边形;
如图,过点作,垂足为点,若,请直接写出图中所有与相等的线段不包括
一汽车销售商店经销,两种型号轿车,用万元购进型轿车辆和型轿车辆;用万元可以购进型轿车辆,型轿车辆.
求型、型轿车每辆进价分别为多少万元?
若该汽车销售商店购进、两种型号的轿车共辆,且购车资金不超过万元,该汽车销售商店至少购进型轿车几辆?
如图,菱形,连接对角线,过点作于点,交于点,连接,若.
如图,求证:;
如图,连接,求证:;
如图,过点作的垂线,分别交延长线于点、延长线于点,若,,求:的值.
如图,在平面直角坐标系中,点为坐标原点,直线分别交轴正半轴于点,交轴负半轴于点,过点作,且.
求点的坐标.
过点作轴,垂足为,是线段上一个动点,过点作轴,垂足为点,在延长线上取点,在轴点右侧取点,连接,在线段上取点,连接,使,设线段,满足的面积表示为,求线段的长度.
在的条件下,连接并延长交轴于点,当为中点时,连接,过点作,在轴左侧直线上是否存在点,连接、,使得与以、、为三边长的三角形全等?若存在,求出的长,若不存在,请说明理由.
答案和解析
1.【答案】
【解析】解:、矩形是轴对称图形,又是中心对称图形,故选项错误;
B、菱形既是轴对称图形,又是中心对称图形,故选项错误;
C、正方形是轴对称图形,又是中心对称图形,故选项错误;
D、平行四边形是中心对称图形,不是轴对称图形,故选项正确;
故选:.
根据中心对称图形以及轴对称图形的定义即可作出判断.
本题主要考查了中心对称图形与轴对称图形的定义,正确理解定义是解题关键.
2.【答案】
【解析】解:、,故A不符合题意;
B、,故B符合题意;
C、,故C不符合题意;
D、,故D不符合题意;
故选:.
利用幂的乘方与积的乘方的法则,同底数幂的乘法的法则,同底数幂的除法的法则对各项进行运算即可.
本题主要考查幂的乘方的与积的乘方,同底数幂的乘法,同底数幂的除法,解答的关键是对相应的运算法则的掌握.
3.【答案】
【解析】解:在中,,是的中点,
线段是斜边上的中线;
又,
.
故选:.
根据直角三角形斜边上的中线等于斜边的一半解答.
本题考查了直角三角形斜边上的中线.熟记直角三角形斜边上的中线等于斜边的一半是解题的关键.
4.【答案】
【解析】解:菱形的面积:,
故选:.
根据菱形的面积公式:菱形面积、是两条对角线的长度可得到答案.
此题主要考查了菱形的面积公式,关键是熟练掌握面积公式.
5.【答案】
【解析】解:由勾股定理得:,
故选:.
根据勾股定理求出即可.
本题考查了勾股定理的应用,能熟记勾股定理的内容是解此题的关键.
6.【答案】
【解析】解:菱形中,如果、、、分别是各边的中点,
由中位线定理可得,所得四边形的对边平行且相等,则此四边形为平行四边形;
又因为菱形的对角线互相垂直平分,可求得四边形的一角为,
所以连接菱形各边中点的四边形是矩形,
即四边形的形状是矩形.
故选:.
利用中点四边形的定义得出,以及矩形的判定:有一角为的平行四边形是矩形,得出菱形中点四边形的形状.
此题主要考查了矩形的判定定理:有一个角是直角的平行四边形是矩形;有三个角是直角的四边形是矩形;对角线互相平分且相等的四边形是矩形.
7.【答案】
【解析】解:去分母得:,
解得:,
检验:把代入得:,
分式方程的解为.
故选:.
分式方程去分母转化为整式方程,求出整式方程的解得到的值,经检验即可得到分式方程的解.
此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.
8.【答案】
【解析】解:过作于,交于,
四边形是正方形,
,,
,
,
,
,,
,
故选:.
方法二:,
,
,
,
四边形是正方形,
,
,
,
故选:.
过作于,交于,证得,根据三角形外角定理即可求出.
本题主要考查了正方形的性质,直角三角形的两锐角互余,根据直角三角形的两锐角互余证得是解决问题的关键.
9.【答案】
【解析】解:,,
.
将沿折叠,使点与点重合,
.
,,,
≌.
,,
.
,即.
故选:.
本题主要考查的是翻折的性质、勾股定理的应用,利用翻折的性质得到从而证出≌,根据勾股定理,含角的直角三角形的性质即可求得.
10.【答案】
【解析】解:、对角线相等且互相平分的四边形是矩形,本选项说法是真命题;
B、一组对边平行一组对角相等的四边形是平行四边形,本选项说法是真命题;
C、一条对角线平分一组对角的平行四边形是菱形,本选项说法是真命题;
D、对角线互相平分且互相垂直的四边形是菱形,本选项说法是假命题;
故选:.
根据矩形、平行四边形、菱形的判定定理判断即可.
本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
11.【答案】
【解析】解:将写成科学记数法的形式为.
故答案为:.
绝对值小于的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的的个数所决定.
12.【答案】
【解析】解:
,
故答案为:.
先提公因式,然后利用平方差公式分解即可解答.
本题考查了提公因式法与公式法的综合运用,一定要注意如果多项式的各项含有公因式,必须先提公因式.
13.【答案】
【解析】解:,,
四边形是平行四边形,
四边形是矩形,
,,,
,
四边形是菱形,
,
四边形的周长;
故答案为:.
先证明四边形是平行四边形,再根据矩形的性质得出,然后证明四边形是菱形,即可求出周长.
本题考查了菱形的判定与性质以及矩形的性质;证明四边形是菱形是解决问题的关键.
14.【答案】
【解析】解:四边形是正方形,是等边三角形,
,,
,
,
,
.
,
故答案为:.
先证明为等腰三角形,从而可取得的度数,然后依据三角形内角和定理求出的度数,进而可以解决问题.
本题主要考查的是正方形的性质、等边三角形的性质、等腰三角形的性质,熟练掌握相关图形的性质是解题的关键.
15.【答案】
【解析】解: 中,,,
,,
,
,
是直角三角形,即,
.
故答案为:.
由 中,,,,求得,的长,利用勾股定理的逆定理即可证得是直角三角形,继而求得答案.
此题考查了平行四边形的性质以及勾股定理的逆定理.注意证得是直角三角形是关键.
16.【答案】
【解析】解:,,,
,
,
则,
,
,
,
是斜边的中点,
,
,
,
故答案为:.
先根据已知条件求出和的度数,再根据是斜边的中点,得出,从而得出结论.
本题考查了直角三角形斜边上的中线的性质以及角的运算,关键是对角的和差的运算.
17.【答案】
【解析】解:连接,如图,
和都是等腰直角三角形,,,
,,,
,
在和中,
,
≌,
,,
,
是直角三角形,
,
是等腰直角三角形,,
,
,
解得:负值已舍去,
故答案为:.
连接,证≌,得,,再证证明是直角三角形,然后由勾股定理求出的长,即可得出的长.
本题考查了全等三角形的判定与性质、等腰直角三角形的性质、勾股定理等知识,熟练掌握等腰直角三角形的性质,证明三角形全等是解题的关键.
18.【答案】或
【解析】解:如图所示:
作于点,则,
四边形为矩形,
,,
四边形为矩形,
,
,
,
,
,
,
;
如图所示:
作于点,则,
四边形为矩形,
,,
四边形为矩形,
,
,
,
,
,
,
,
故答案为:或.
根据矩形的性质和勾股定理,分两种情况解答即可.
此题考查矩形的性质,关键是根据矩形的性质得出对边相等解答.
19.【答案】
【解析】解:取的中点,连接,,
为的中点,
是的中位线,
,,
为的中点,
是的中位线,
,,
,
,
,
,
,即,
,
故答案为:.
取的中点,连接,,理由三角形的中位线可求解,结合可得,再利用勾股定理可求解的长.
本题主要考查三角形的中位线,勾股定理,求解,的值是解题的关键.
20.【答案】
【解析】解:,
,,,四点共圆,
,
,
,
,
,
作于点,
,
≌,
,,
,,
≌,
,
,
即,
设,,
,,
,
,
在中,,
即,
解得:,
,,
,
,
故答案为:.
根据全等三角形的判定和性质得出,,进而利用勾股定理解答即可.
此题考查全等三角形的判定和性质,关键是根据全等三角形的判定和性质解答.
21.【答案】解;原式
,
当时,原式.
【解析】先根据分式混合运算的法则把原式进行化简,再把的值代入进行计算即可.
本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.
22.【答案】
【解析】解:如图中,菱形即为所求.
如图中,平行四边形即为所求.
图中平行四边形较短的一条对角线的长度为.
故答案为:.
构造边长为的菱形即可;
构造底为,高为,有一个角是的平行四边形即可;
根据网格利用勾股定理即可求出图中平行四边形较短的一条对角线的长度.
本题考查作图应用与设计,平行四边形的判定和性质,菱形的判定和性质等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.
23.【答案】解:由已知可得:海里,
又已知甲船以海里时的速度沿北偏东方向航行,乙船沿北偏西,
,
又乙船正好到达甲船正西方向的点,
,
海里,
所以乙船的速度为:海里小时,
答:乙船的速度为海里小时.
【解析】本题可以求出甲船行进的距离,根据三角函数就可以求出,就可以求出乙船的速度.
本题主要考查的是解直角三角形的应用方向角问题及三角函数的定义,理解方向角的定义是解决本题的关键.
24.【答案】解:如图中,
四边形是平行四边形,
,,
点,分别为边,的中点,
,,
,,
四边形是平行四边形.
如图中,连接
,,
四边形是矩形,
,
四边形是矩形.
,,
,,
与相等的相等有,,,,.
【解析】只要证明,即可;
如图中,连接首先证明四边形是矩形.推出由,,可得,;
本题考查平行四边形的判定和性质、矩形的判定和性质、直角三角形斜边中线定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
25.【答案】解:设型号的轿车每辆进价为万元,型号的轿车每辆进价为万元.
根据题意得,
解得.
答:设型号的轿车每辆进价为万元,型号的轿车每辆进价为万元.
设汽车销售商店至少购进型轿车辆,则型轿车辆,由题意得,
,
解得:.
答:该汽车销售商店至少购进型轿车辆.
【解析】等量关系为:辆轿车的价钱辆轿车的价钱万元;辆轿车的价钱辆轿车的价钱万元;
根据中求出、轿车的单价,然后根据关键语“用不超过万元购进、两种型号轿车共辆”列出不等式,解出不等式即可.
此题考查二元一次方程组和一元一次不等式的运用,找出题目蕴含的数量关系是解决问题的关键.
26.【答案】证明:设,
四边形是菱形,
,,
,
,,
,
,
,
,
;
证明:四边形是菱形,
,,
又,
≌,
,
;
解:,,
,
,
四边形是平行四边形,
,
,
,
,
,
,
,
,
,,
,
,
,
,
:.
【解析】由菱形的性质可得,由余角的性质可求,可得;
由“”可证≌,可得,可得结论;
利用勾股定理和面积法分别求出,,的长,即可求解.
本题是四边形综合题,考查了菱形的性质,全等三角形的判定和性质,勾股定理等知识,利用勾股定理计算出的长是解题的关键.
27.【答案】解:如图,点,交轴负半轴于点,
,,
过点作轴于,则,
,
,
,
,
,
,
≌,
,,
,
;
如图,,
,
,
,
轴,
,
,
,
的面积为,
,
;
在轴左侧直线上是存在点,使得与以、、为三边长的三角形全等,
如图,
轴,轴,
,
是直角三角形,
与以、、为三边长的三角形全等,
、、构成的三角形为直角三角形,
过点作轴于,则,由知,,
,
轴,轴,
,
轴,
轴,
,
为中点,
,
≌,
,
,
由知,,
,
记与轴的交点为,则四边形为矩形,
,
,
,
点在线段上,
,
,
是公共边,
与是对应边,且是斜边,即,
设,则点,,
,,
、、构成的三角形为直角三角形,
,
,
,
,
即:.
【解析】过点作轴,进而判断出≌,得出,,即可求出答案;
先判断出,进而判断出,再用的面积为建立方程求解,即可求出答案;
先判断出、、构成的三角形为直角三角形,过点作轴于,进而判断出≌,得出,求出,由知,,,记与轴的交点为,则四边形为矩形,进而求出,,进而判断出,进而判断出与是对应边,且是斜边,设,表示出点,的坐标,再利用勾股定理建立方程求出的值,即可求出答案.
此题是一次函数综合题,主要考查了全等三角形的判定和性质,三角形的面积公式,等腰直角三角形的性质,勾股定理,判断出为斜边是解本题的关键.
第2页,共2页
第1页,共1页
同课章节目录
